Equipo Parramón Paidotribo - Matemáticas y Física & Química

Una empresa de chocolates fabrica bombones envueltos en papel rojo, que se venden en cajas de doce, y bombones envueltos en papel azul, que se venden en cajas de ocho. ¿Se podrán trasladar los bombones a cajas más pequeñas, que sólo contengan bombones rojos o azules?

Para que no sobre ningún bombón, la capacidad de estas cajas tiene que ser un número divisor de ocho y también de doce.

La descomposición factorial de ocho es: 8 = 2 · 2 · 2 = 2 3

El doce, por su parte, se descompone así: 12 = 2 · 2 · 3 = 2 2· 3

Si tomamos los factores comunes elevados al menor exponente posible, obtenemos: 2 2= 4. El cuatro es el mayor de los números que dividen tanto a ocho, como a doce. Luego sólo podemos trasladar los bombones a cajas de uno, de dos o de cuatro.

El veintiocho es un número perfecto. Sus divisores son 1, 2, 4, 7, 14 y 28. Entonces, tenemos: 1 + 2 + 4 + 7 + 14 = 28.

Se dice que un número es perfecto, cuando coincide con la suma de sus divisores, exceptuando a él mismo.

El máximo común divisor es el mayor de los divisores comunes a varios números.

MÍNIMO COMÚN MÚLTIPLO

Marta come legumbres cada seis días y su hija Ana, en el comedor del colegio, cada cuatro. Si hoy ambas han tomado legumbres, ¿cuándo volverán a coincidir?

La descomposición factorial de seis es: 6 = 2 · 3 y la de cuatro es 4 = 2 · 2 = 2 2. Si tomamos los factores comunes elevados al mayor exponente posible y los factores que no son comunes, obtenemos: 2 2· 3 = 12. Luego volverán a coincidir dentro de doce días.

El mínimo común múltiplo es el menor de los múltiplos comunes a varios números.

NÚMEROS ENTEROS

María entra en un ascensor en la quinta planta de un edificio. Como quiere ir al séptimo piso, tiene que subir dos pisos, puesto que 7 = 5 + 2. Si hubiera querido bajar tres pisos, también habría podido hacerlo, ya que 5 – 3 = 2. ¿Pero podría haber bajado siete pisos? No.

Supongamos ahora que estamos en otro edificio en el que hay tres sótanos destinados a aparcamiento y que en el ascensor están señalados con los números –1, –2 y –3. ¿Podríamos bajar siete pisos estando en el quinto? Al contar con números negativos, sí que podríamos hacerlo: 5 – 7 = –2, es decir, acabaríamos en el segundo sótano.

LOS QUIPU

Los incas utilizaban un sistema de cuerdas, denominado “quipu”, a las que hacían determinados nudos para realizar sus cálculos.

REPRESENTACIÓN GRÁFICA DE LOS NÚMEROS ENTEROS

Para dibujar los números enteros en una recta, seguimos el siguiente proceso:

•Situamos el cero en un punto cualquiera.

•Tomamos una medida cualquiera y la vamos llevando hacia la derecha del cero, representando así a los números enteros positivos, que coinciden con los naturales.

•Vamos llevando la misma medida hacia la izquierda del cero para dibujar los enteros negativos.

EL ORIGEN DEL NÚMERO CERO

Muchas civilizaciones de la antigüedad no utilizaban el cero. ¿Para qué contar un rebaño que no tiene ninguna oveja? ¿Para qué representar con un símbolo a la nada? Pero, ¿cómo escribir el número 408 sin emplear el cero? Los pueblos que usaban sistemas de numeración posicionales lo resolvían dejando un espacio en blanco entre el cuatro y el ocho. Con este método se solían confundir los números 48, 408 y 480, y por esta razón los hindúes optaron por colocar un punto donde antes dejaban un espacio en blanco. Con el paso del tiempo, el punto se convirtió en un círculo.

Los chinos operaban con un ábaco de dos colores: el rojo para los números positivos y el negro para los negativos. En la fotografía, ábaco gigante en una calle de Cesis (Letonia).

LOS NEGATIVOS

Aunque chinos e hindúes han utilizado números negativos desde hace más de mil años, en Europa no empezaron a emplearse hasta el Renacimiento y no fueron totalmente admitidos hasta finales del siglo XIX.

Se llama valor absoluto de un número entero al número natural que resulta al omitir el signo. El valor absoluto se representa con dos barras verticales: |–3| = 3.

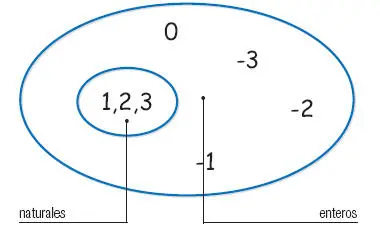
Los naturales, el cero y los negativos constituyen el conjunto de los números enteros.

SUMA DE ENTEROS

Para jugar a la suma de enteros, construyamos un tablero de cartón que tenga treinta y una zonas: quince zonas llevan números negativos, –1 al –15; quince llevan números positivos; la zona central corresponde al cero. Dispongamos también de una ficha y de un dado. Las reglas del juego:si llegas a la zona 15, enhorabuena, habrás logrado un gol; si retrocedes a la zona –15, lo sentimos, habrás encajado un gol.

Para sumar dos enteros que tengan el mismo signo, se suman los valores absolutos y se añade dicho signo.

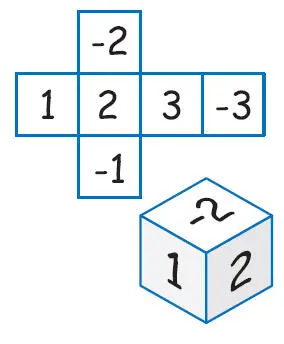
Las caras del dado del juego de la suma de enteros contienen los números 1, 2, 3, –1, –2 y –3.

RESTA DE ENTEROS

Para restar dos enteros se suma al primero el opuesto del segundo:

2 – (–3) = 2 + 3 = 5

3 – (5) = 3 + (–5) = –2

Se llama opuesto de un número al que tiene el mismo valor absoluto, pero distinto signo. Así el opuesto del 3 es el –3 y el opuesto del –5 es el 5.

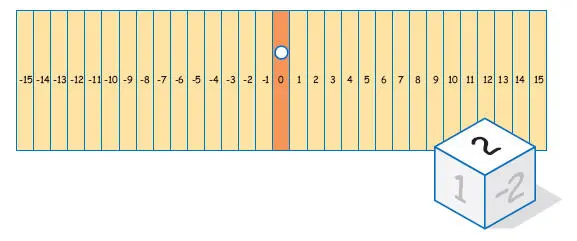
situemos la ficha en la zona cero y lancemos el dado; supongamos que sale un dos

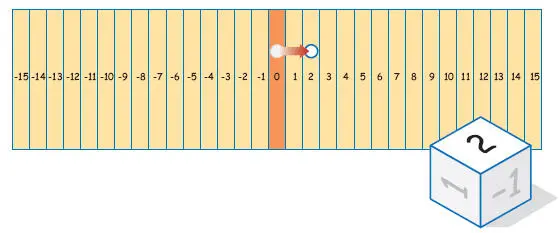
moveremos la ficha a la zona dos

Para sumar dos enteros que tengan distinto signo, se restan los valores absolutos y se añade el signo del que tenga mayor valor absoluto.

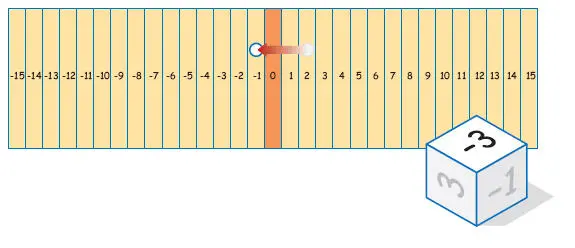
lancemos de nuevo y supongamos que salga un –3; moveremos la ficha tres casillas hacia la izquierda y acabaremos en la zona –1. Matemáticamente podemos representar este movimiento así: 2 + (– 3) = –1