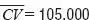Equipo Parramón Paidotribo - Matemáticas y Física & Química

Nuestro siguiente tema será la geometría plana, es decir la que estudia las figuras en dos dimensiones.

Echaremos un vistazo a la trigonometría, que se ocupa de las relaciones existentes entre los ángulos y las distancias, y que resulta fundamental en el campo de las modernas telecomunicaciones. Nos adentraremos entonces en el estudio de los cuerpos geométricos que pueblan el espacio de tres dimensiones.

Nuestra siguiente etapa constituirá una iniciación a la estadística. Ordenaremos datos, dibujaremos gráficos, hallaremos parámetros y aprenderemos a calcular probabilidades.

No nos gustaría acabar este viaje sin acercarnos a descubrir cuál es el presente y el futuro próximo de la matemática y a conocer algunos retos a los que se enfrenta la matemática de nuestros días, tales como el desarrollo de la teoría del caos, de la geometría fractal o de la lógica borrosa.

Las gráficas nos permiten representar datos (cualitativos, de ordenación o cuantitativos) mediante una construcción que facilita evaluarlos visualmente de manera rápida y comprensiva.

SISTEMAS DE NUMERACIÓN

Gracias a los hallazgos arqueológicos y al estudio de los pueblos que viven aún de forma primitiva, sabemos que nuestros antepasados empleaban diversos sistemas para contar y ordenar los objetos. Lo hacían con los dedos, agrupando pequeñas piedras o realizando marcas en huesos y troncos de árboles. El resto más antiguo que se ha encontrado es un hueso de lobo con 55 incisiones, hallado en Europa Central y que tiene unos 50.000 años de antigüedad.

EL SISTEMA DECIMAL

Nuestro sistema de numeración tiene tres propiedades:

•Utilizamos diez símbolos diferentes para escribir los números: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Por esta razón se dice que es un sistema decimalo de base diez. Diez unidades se agrupan en una decena; diez decenas, en una centena y así sucesivamente. Todo número, por tanto, se puede expresar en forma de potencias de diez:

4.546 = 4 · 1.000 + 5 · 100 + 4 · 10 + + 6 = 4 · 10 3+ 5 · 10 2+ 4 · 10 + 6.

•El valor de cada símbolo depende de la posición que ocupa. Por eso decimos que es un sistema posicional. Así, por ejemplo, en el número anterior, el cuatro situado a la izquierda vale cuatro mil mientras que el otro vale cuarenta.

•Es un sistema completo, puesto que emplea el cero.

Los números romanos siguen apareciendo en muchos lugares.

Tanto la civilización azteca como la maya alcanzaron un nivel de conocimientos matemáticos muy elevado. Utilizaban sistemas de numeración posicionales, pero que no eran decimales. En la fotografía, Gran Pirámide de Chichén Itzá (México).

LOS NÚMEROS ROMANOS

Los romanos empleaban siete letras para escribir los números. Sus valores eran: I = 1, V = 5, X = 10, L = 50, C = 100, D = 500 y M = 1.000.

Es un sistema de numeración no posicional, que todavía se utiliza para escribir los siglos. También podemos encontrar números romanos en los monumentos conmemorativos y en las esferas de algunos relojes. Para leerlos, tenemos que seguir las reglas siguientes:

•Si encontramos una letra situada a la derecha de otra de mayor valor, las sumaremos:

MDL = 1.000 + 500 + 50 = 1.550

•Cuando una letra está situada a la izquierda de otra de mayor o igual valor, tendremos que restarlas:

XC = 100 – 10 = 90

•En el caso de que un grupo de letras esté situado debajo de una raya, multiplicaremos su valor por mil:

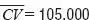
Equivalencia del sistema binario y del sistema decimal.

El sistema binario se utiliza en informática y telecomunicaciones.

EL SISTEMA BINARIO

En este sistema se emplean sólo dos símbolos: el cero y el uno. Para traducir un número binario emplearemos las potencias de dos:

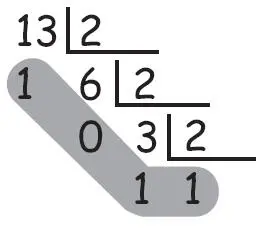
1.101 = 1 · 2 3+ 1 · 2 2+ + 0 · 2 + 1 = 8 + 4 + 0 + 1 = 13.

Para escribir un número en forma binaria tenemos que dividirlo sucesivamente por dos:

EL SISTEMA SEXAGESIMAL

Para medir el tiempo y los ángulos, usamos un sistema de base sesenta heredado de los babilonios. Sesenta segundos forman un minuto y sesenta minutos una hora o un grado.

Las cifras o números que utilizamos actualmente se suelen conocer como cifras árabes, pues fueron los árabes quienes las introdujeron en Europa en el siglo X a través de la España musulmana. Al parecer, los árabes tomaron este sistema de numeración de la India.

La esfera de un reloj está dividida en 12 partes. Cada una de éstas se subdivide a su vez en 5 partes, de forma que 12 · 5 = 60.

NÚMEROS NATURALES

Si preguntamos a un niño de dos años cuántos años tiene, posiblemente nos contestará extendiendo dos dedos. Los números naturales (1, 2, 3, 4, 5, ...) son los primeros que aprendemos e, históricamente, fueron los primeros en aparecer. Estudiaremos las operaciones matemáticas que se efectúan con ellos y descubriremos que son absolutamente insuficientes, puesto que en muchos casos dichas operaciones no podrán realizarse.

Con los números naturales podemos confeccionar códigos identificativos, como los códigos de barras.

Si los utilizamos para ordenar los elementos de un conjunto, se llaman primero, segundo, tercero, cuarto, etc.

Los números naturales se emplean para contar.

SUMA DE NÚMEROS NATURALES