Hebert Vázquez - Fundamentos teóricos de la música atonal

En el pentagrama inferior encontramos un conjunto cuya presencia domina los compases 4 al 8; se trata del conjunto de c.a. {2, 6, 8, 9, A, B}, al que llamaremos conjunto Y, y que, también en este caso, aparece en tres ocasiones. En los compases 7 y 8, entre la segunda y tercera aparición del conjunto Y , se encuentran las c.a. 1 y 0 que no pertenecen al mismo y que dejaremos a un lado por el momento. Se puede observar que, a diferencia del conjunto X, el conjunto Y presenta siempre sus elementos en el mismo orden (y con los mismos valores de duración) en sus diferentes apariciones.12

RELACIONES ENTRE CONJUNTOS EN LOS COMPASES 4 Y 5 DEL OP. 11, Nº1, DE SCHOENBERG

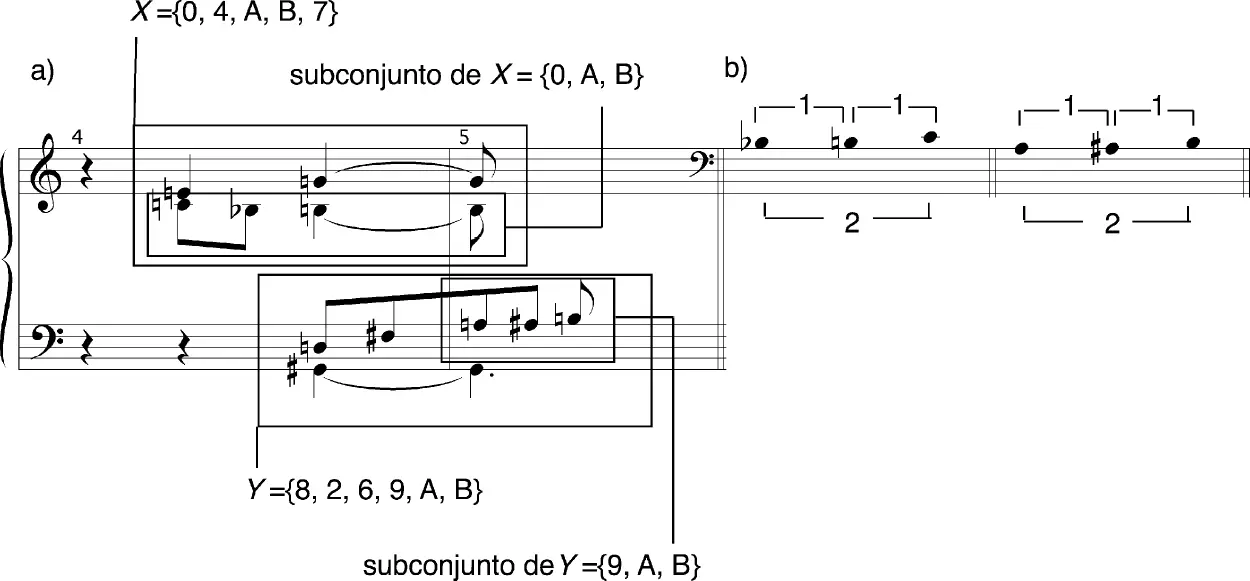
Existen varios puntos de contacto entre el conjunto X y el conjunto Y. Uno de ellos, por supuesto, es que comparten las c.a. A y B. En el ejemplo 24 a), que muestra la aparición de ambos conjuntos en los compases 4 y 5, se puede apreciar cómo éstos generan un subconjunto de tres notas que incluye, en ambos casos, las c.a. A y B. El subconjunto del conjunto X abarca la totalidad de la voz inferior, mientras que el subconjunto de Y comprende las tres últimas notas de la voz superior. En el ejemplo 24 b) se presentan ambos subconjuntos en su disposición más compacta, lo que nos permite apreciar que tienen la misma estructura interválica. El nexo entre los mismos se ve reforzado, además, debido a que las dos c.a. que comparten —las c.a. A y B—, se encuentran en el mismo índice acústico en todas sus apariciones (si transferimos estas c.a. al espacio-a se convertirán en A4 y B4 en los dos subconjuntos) y, en el caso particular de los compases 4 y 5 (ejemplo 24 a)), se suceden en forma directa.

Otro nexo importante entre los conjuntos X e Y se evidencia en los compases 7 y 8 en donde, debido a una nueva disposición de los elementos del conjunto X, queda al descubierto un subconjunto formado por una tríada mayor, que es expuesta en forma imitativa por los dos conjuntos, como se puede observar en el ejemplo 25. Es importante señalar que las diferentes relaciones en el subconjunto que han surgido entre los conjuntos X e Y se deben a las redistribuciones de los elementos del conjunto X en sus diversas apariciones.

RELACIONES ENTRE CONJUNTOS EN LOS COMPASES 7 Y 8 DEL OP. 11, Nº1 DE SCHOENBERG

Como se comentó anteriormente, en el compás 7 aparecen las c.a. 1 y 0, a las que hemos considerado ajenas a los conjuntos X e Y debido a que no se encuentran presentes en las otras apariciones de dichos conjuntos. En el ejemplo 26 a) podemos ver que al unir dichas c.a. con el Re natural del conjunto Y, se crea un nuevo conjunto {1, 0, 2}. El ejemplo 26 b) nos muestra que el nuevo conjunto presenta la misma estructura interválica que los subconjuntos analizados en el ejemplo 24 b). Finalmente, en el ejemplo 26 c) las flechas muestran que el nuevo subconjunto {1, 0, 2}, localizado en el pentagrama inferior, es una imitación retrógrada al intervalo -A0, del conjunto de la línea inferior de X; esta relación explica la inversión del orden y del valor numérico de sus respectivos intervalos ordenados de altura.

IMITACIÓN RETRÓGRADA ENTRE LOS ELEMENTOS DE DOS CONJUNTOS (ARNOLD SCHOENBERG. DREI KLAVIERSTÜCKE, OP. 11: Nº 1, CC. 7-8)

Por último, cabe preguntarse si existirá algún tipo de conexión entre el material de los compases 1-3 y el de los compases 4-8. La respuesta se encuentra en los compases 4 y 5. Aquí se puede observar que las c.a 7 y B en el pentagrama superior y la c.a. 8 en el pentagrama inferior corresponden a las c.a. del conjunto de las tres primeras notas de la pieza (ver los ejemplos 22 y 23 a)). Además, en los compases 7 y 8 las tres c.a. se encuentran claramente relacionadas al ser atacadas al mismo tiempo y mantenerse sonando hasta el siguiente compás, mientras que todas las notas a su alrededor duran únicamente un octavo (con la única excepción del Mi del compás 4 que dura un cuarto). Obsérvese, también, que las tres c.a. no volverán a estar relacionadas con tanta claridad en las dos siguientes apariciones de los conjuntos X e Y (ver ejemplo 22). Resulta claro que Schoenberg buscó establecer la conexión más fuerte entre los materiales contrastantes de los compases 1-3 y 4-8 en el momento mismo de la transición entre dichos materiales, asegurando así el punto de unión entre ambas secciones.

Esta introducción informal al manejo de conjuntos ha pretendido servir de punto de contacto con respecto a algunas relaciones básicas que se pueden establecer entre los mismos, con el propósito de sugerirle al lector su importancia estructural en el pensamiento musical atonal. En este capítulo y los siguientes, procederemos a tratar éstas y otras relaciones en forma un poco más detallada y rigurosa.

Antes de abordar los diferentes tipos de relaciones que se dan entre los conjuntos, será conveniente definir el conjunto y sus elementos, establecer el concepto de cardinalidad y conocer algunos tipos de conjuntos básicos como el agregado, el universo, y el conjunto vacío.

Los conjuntos de clases de alturas, a los que podemos llamar simplemente conjuntos, se utilizan para representar sonoridades en el espacio-c.a. Un conjunto es una colección de clases de alturas no ordenadas y escritas sin repeticiones.

Normalmente, se usan letras mayúsculas para representar los conjuntos. En contextos en los cuales la notación pudiera resultar ambigua, es recomendable evitar aquellas letras que en la teoría atonal representan operaciones o entidades ajenas a los conjuntos, tales como A, B, C, D, E, F, G, que podrían ser confundidas con alturas o clases de alturas, o también T, I, U, M, P, R, V, cuyo significado se irá revelando en este libro.

Los elementos de los conjuntos se delimitan por medio de llaves ({·}) y pueden escribirse de corrido o separados por medio de comas o espacios. Por ejemplo, dado un conjunto Y que contenga las c.a. 0, 1 y 3, dicho conjunto puede aparecer representado en cualquiera de las siguientes maneras: Y = {013}; Y = {0 1 3}; Y = {0, 1, 3}.

EL CONJUNTO COMO REPRESENTACIÓN DE UNA SONORIDAD

(MARIO LAVISTA, SIMURG, PARA PIANO: A) = CC. 1-2, B) = CC. 44-45. C) = CC. 48. D) = CC. 62, E) = CC. 64)

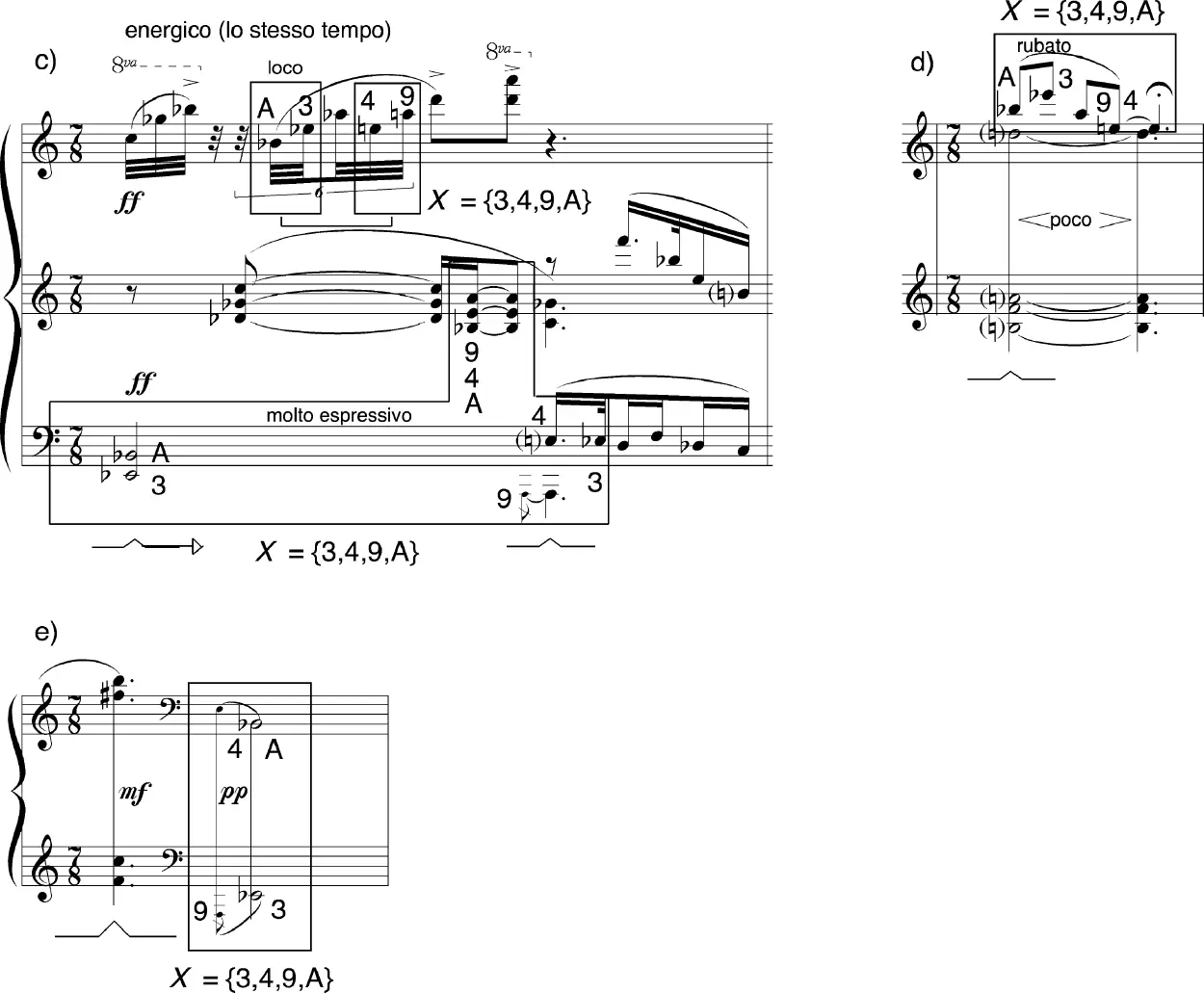
En este ejemplo se presentan varios extractos de una pieza para piano de Mario Lavista. En el primer compás de la obra se expone, en el bajo, un fragmento de cuatro notas al que clasificaremos como el conjunto X = {3,4,9,A}. Dicho conjunto representa el cimiento sobre el cual se erguirá toda la arquitectura de la pieza, como nos deja ver claramente el compositor al presentarlo al inicio de la obra, aislado de cualquier interferencia sonora. Durante los primeros diez compases de la pieza, el conjunto X será tratado como un ostinato , monopolizando la parte del bajo (los primeros dos compases del ostinato aparecen en el ejemplo 27 a)). Sin embargo, se podrá apreciar en el ejemplo que, lejos de permanecer limitado al bajo, X hace su aparición en prácticamente todas las voces, registros y disposiciones imaginables: se le puede ver desplegado en forma lineal, armónica o mixta; con o sin repetición de clases de alturas; presentado en forma contigua o fracturada (este último caso se puede apreciar en la voz superior del ejemplo 27 c) donde X aparece escindido por la c.a. 8, que no forma parte del conjunto); localizado en una o varias voces; con valores de duración largos o muy breves (como en el caso de las notas de adorno del ejemplo 27 a)); limitado a un registro reducido o esparcido a lo largo de dos o más octavas, etc. Lo importante es que, independientemente de la forma en que sea presentado, el conjunto X puede ser reducido conceptualmente a una entidad sonora única al ser clasificado como X = {3,4,9,A}. Con lo anterior, se le despoja de atributos tales como el ritmo, registro, disposición o repetición de sus elementos y se le convierte en una abstracción de su sonoridad básica, establecida en función de la simple enumeración de las clases de alturas que lo componen.