Hebert Vázquez - Fundamentos teóricos de la música atonal

y mód. 12 significa que lo que está entre paréntesis se calcula por medio de la aritmética mód. 12.

Los dos resultados anteriores se pueden condensar en la siguiente fórmula: i.s.< a c, b d> = S((-1)| b - a |) mód. 12|d - c| - (1)

donde (-1) indica que se multiplica por -1 si y sólo si tenemos un caso mixto.

-(1) indica que se resta -1 si y sólo si tenemos un caso mixto.

Digamos que nos interesa obtener el intervalo simplificado entre las alturas <56, A5>. Se puede apreciar que 5 < A y 6 > 5, por lo que estamos ante un caso mixto. Procedemos entonces a sustituir las variables de la fórmula correspondiente al caso mixto por las alturas 56 y A5: i.s.<56, A5> = S(-|A - 5|) mód. 12|5 - 6| - 1. Al realizar las operaciones indicadas obtenemos: S(-|5|) mód. 12|-1| - 1. Ahora bien, -5 (mód. 12) = -5 + 12 = 7 y, en lo que respecta a la operación señalada en el subíndice, tenemos que |-1| - 1 = 1 - 1 = 0, lo que nos da: S(7)0. Sólo resta saber si el intervalo es ascendente o descendente, para lo cual será necesario obtener el valor de S. La definición de caso mixto nos dice que S = sgn ( d - c ), lo que en nuestro caso nos da: S = sgn (5 - 6). Como 5 - 6 = -1, tenemos que S = sgn (-1). Vemos que el signo de -1 es menos (-), por lo que S será sustituido por dicho signo: S(7)0 = -70. Por lo tanto, i.s.<56, A5> = -70, es decir, que para ir de la altura 56 a la altura A5 se debe de descender siete semitonos (y ninguna octava), como se muestra en el ejemplo 18.

i.s. <5 6, A 5>=7 0

En el ejemplo 19 tenemos cuatro intervalos ordenados simplificados que corresponden a cada uno de los casos posibles. Debajo del pentagrama se desglosa el procedimiento para su obtención.

EL INTERVALO ORDENADO SIMPLIFICADO REPRESENTADO EN SUS CUATRO CASOS

Una característica fundamental de la nueva notación es que, independientemente de la extensión que presente el intervalo ordenado, es capaz de expresar con claridad su cualidad sonora. Esto es posible debido a que la variable a en ± a c nos indica cuál es el intervalo simple, ascendente o descendente, que se extiende a lo largo de c octavas, cosa que no sucede con la notación numérica tradicional, más allá de la primera octava de extensión.

El lector habrá notado que la obtención informal del intervalo ordenado simplificado es sencilla. Basta con sumar mentalmente n octavas ascendentes o descendentes, dependiendo de la dirección del intervalo, a la nota de partida hasta ubicarla a menos de una octava de distancia de la nota de arribo, lo que nos da el valor de c en a c; después se obtiene el intervalo simple a .

El intervalo no ordenado simplificado, al igual que el ordenado, se divide en cuatro casos:

Caso 1. Sean las alturas a c, b d. Sean a ≥ b , c ≥ d .

Caso 2. Las mismas alturas. Sean a ≤ b , c ≤ d .

Caso 3 . Las mismas alturas. Sean a > b , c < d (caso mixto).

Caso 4 . Las mismas alturas. Sean a < b , c > d (caso mixto).

α) Para los dos primeros casos: i.s.{ a c, b d} = | b - a ||d - c|

β ) Para los dos casos mixtos: i.s.{ a c, b d} = (-| b - a |) mód. 12|d - c| - 1

Los dos resultados anteriores se pueden condensar en la siguiente fórmula:

i.s.{ a c, b d} = ((-1)| b - a |) mód. 12|d - c| - (1)

donde (-1) indica que se multiplica por -1 si y sólo si tenemos un caso mixto.

-(1) indica que se resta -1 si y sólo si tenemos un caso mixto.

Se puede apreciar que la definición de intervalo no ordenado simplificado es similar a la de intervalo ordenado simplificado, sólo que sin la función sgn (signo). Esto se debe a que dicha función es la que define la dirección ascendente o descendente del intervalo, la cual no opera en el intervalo no ordenado simplificado, ya que éste mide la distancia absoluta entre dos alturas que son consideradas como real o conceptualmente simultáneas.

Nótese que, por definición, i.s.{ a c, b d} = i.s.{ b d, a c}, es decir, que el orden en el cual se escriban las dos alturas es irrelevante (lo que resulta imprescindible dado que éstas son simultáneas). Lo anterior también es posible gracias a la exclusión de la función sgn de la definición del intervalo no ordenado simplificado.

Ahora veamos un ejemplo. Digamos que se desea obtener el intervalo simplificado entre las alturas simultáneas {43, 84}. Vemos que 4 < 8 y 3< 4, lo que nos indica que se trata de un ejemplo del caso 2. Sustituyendo las variables de la fórmula correspondiente a dicho caso por las alturas 43 y 84, se obtiene: i.s.{43, 84} = |8 - 4||4 - 3|. El resultado de las restas anteriores es: i.s.{43, 84} = 41, es decir, que la distancia absoluta entre las alturas 43 y 84 es de cuatro semitonos más una octava.

Se observa que el intervalo no ordenado simplificado, a diferencia de lo que sucedía con el intervalo no ordenado abordado en el punto 1.5, no se expresa con notación de valor absoluto; ésta resulta innecesaria, ya que el intervalo en sí carece de signo por el simple hecho de que la función sgn no figura en su definición.8

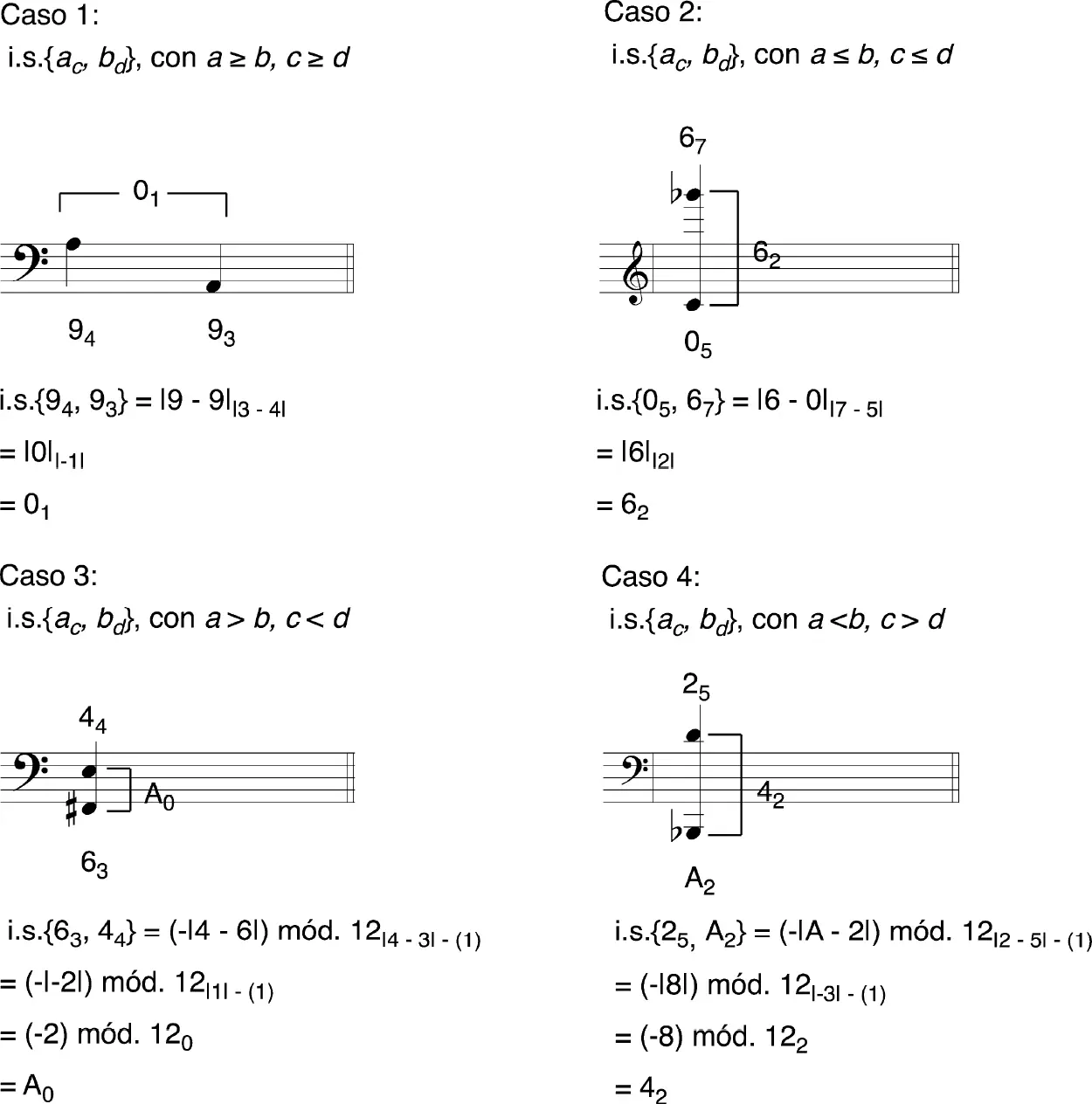
En el ejemplo 21 tenemos cuatro intervalos no ordenados simplificados que corresponden a cada uno de los casos posibles. Debajo del pentagrama se presenta el procedimiento para su obtención. Nótese que en el caso 1 el intervalo simplificado no ordenado es empleado con alturas consecutivas, por lo que éstas son consideradas como “conceptualmente simultáneas”.9

EL INTERVALO NO ORDENADO SIMPLIFICADO REPRESENTADO EN SUS CUATRO CASOS

El rompimiento con la tonalidad llevado a cabo por varios compositores a principios del siglo XX estableció una serie de retos en materia de estructuración sonora. Nuevos medios tuvieron que ser desarrollados con el fin de obtener una coherencia lineal y armónica que fuera independiente de la jerarquía derivada de las funciones armónicas y la conducción lineal del viejo sistema, así como de la omnipotencia de la tríada (a partir de cuya horizontalización, de acuerdo con Schenker, se generan las estructuras tonales en todos los niveles). Ya hacia el final de la primera década del siglo XX, Schoenberg y sus alumnos, Webern y Berg, habían empezado a establecer los fundamentos del nuevo universo sonoro.