Hebert Vázquez - Fundamentos teóricos de la música atonal

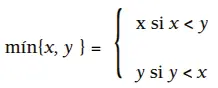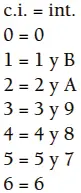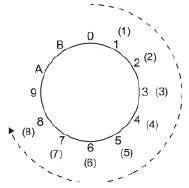
En el caso de i.<0, 8> = 8, el intervalo 8 expresa el desplazamiento de la c.a. 0 a la c.a. 8:

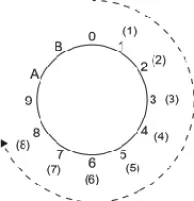
Mientras que en el caso de i.<8, 0> = 4, el intervalo 4 expresa el desplazamiento de la c.a. 8 a la c.a. 0:

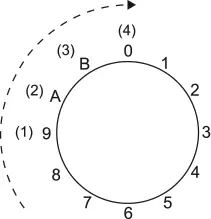
En todos los casos anteriores, los enteros 0, 1, ..., B representan las 12 c.a. del módulo 12 y los enteros entre paréntesis indican el número de semitonos que recorre cada intervalo en su trayecto de una c.a. a otra. Obsérvese que todos los recorridos interválicos entre clases de alturas se llevan a cabo en el sentido de las manecillas del reloj.

Recordemos que el concepto de registro es ajeno a la estructura del espacio-c.a., por lo que el intervalo ordenado i.<6, 8> = 2, por ejemplo, define a cualquiera de los pares de c.a. del ejemplo 11, entre otros.

ALGUNAS DE LAS POSIBILIDADES REPRESENTACIONES EN EL PENTAGRAMA DE LA APLICACIÓN DEL INTERVALO ORDENADO DE CLASE DE ALTURA I.<6, 8>=2

El intervalo no ordenado de clase de altura, también conocido como clase de intervalo o c.i., se utiliza para medir la distancia entre clases de alturas que sean real o conceptualmente simultáneas. Aquí, encontraremos que x - y e y - x nos dan el mismo resultado, como sucedía con los intervalos no ordenados en el espacio-a; sin embargo, en este caso no será necesario recurrir a la notación de valor absoluto para la representación numérica de la c.i., ya que en el espacio-c.a. no hay enteros negativos. Debido a la ausencia del parámetro de registro, producida por la distribución circular del espacio-c.a., se recurrirá siempre a la distancia más pequeña entre dos sonidos simultáneos para representar su clase de intervalo. Por lo tanto, ahora diremos que x - y e y -x pertenecerán ambos a la clase de intervalo z, de forma que z sea igual al que resulte menor de los dos intervalos x - y e y - x, dentro del mód. 12. Podemos representar lo anterior definiendo el mínimo de dos cantidades; dados los intervalos x e y, tenemos que:

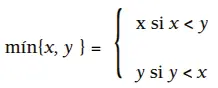
Por ejemplo el mín{3, 7} = 3, ya que 3 < 7. Ahora podemos definir la clase de intervalo entre las c.a. x e y como: i.{ x, y } = mín{i.< x, y >, i.< y, x >}. Nótese que aquí, al igual que en el espacio-a, se está definiendo el intervalo no ordenado en función del intervalo ordenado5

GENERACIÓN DE LA C.I. A PARTIR DEL PRINCIPIO DEL “INTERVALO MÁS PEQUEÑO”

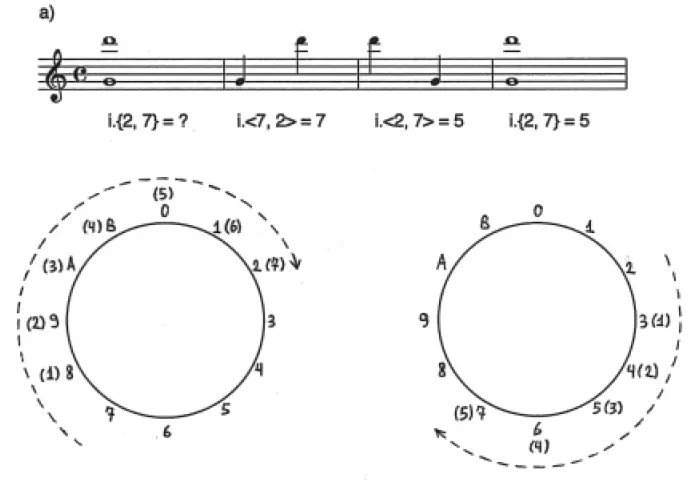
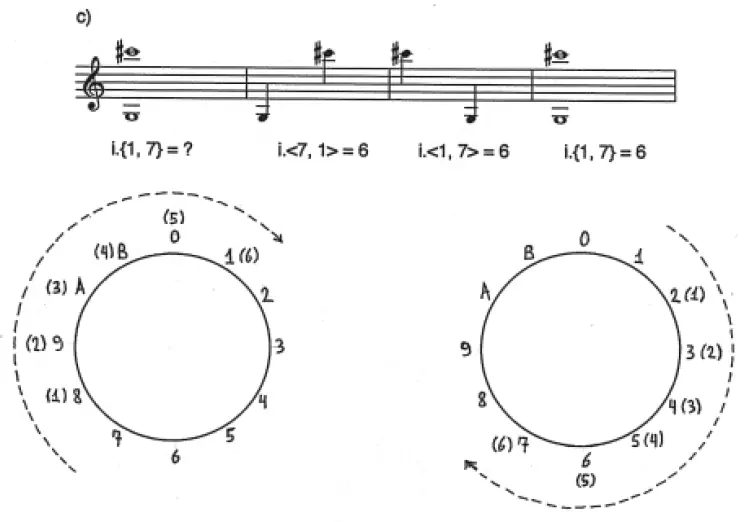
En el ejemplo 12 a) se ilustra el proceso para la obtención de la clase de intervalo entre las c.a. simultáneas 2 y 7 que aparecen en el primer compás. En los compases 2 y 3 se muestran los dos ordenamientos posibles que pueden tener dichas c.a., así como los intervalos ordenados que generan. Podemos apreciar que mín{i.<7, 2>, i.<2, 7>} = 5, ya que 5 < 7, por lo que 5 es la c.i. que mapea entre sí a las c.a. del compás 1, como se señala en el compás 4 del mismo ejemplo 12 a). Los intervalos ordenados i.<7, 2> = 7; i.<2, 7> = 5 (representados ambos por la c.i. 5) correspondientes a los compases 2 y 3, respectivamente, se encuentran también expresados de manera gráfica en el universo circular del espacio-c.a., debajo del pentagrama.

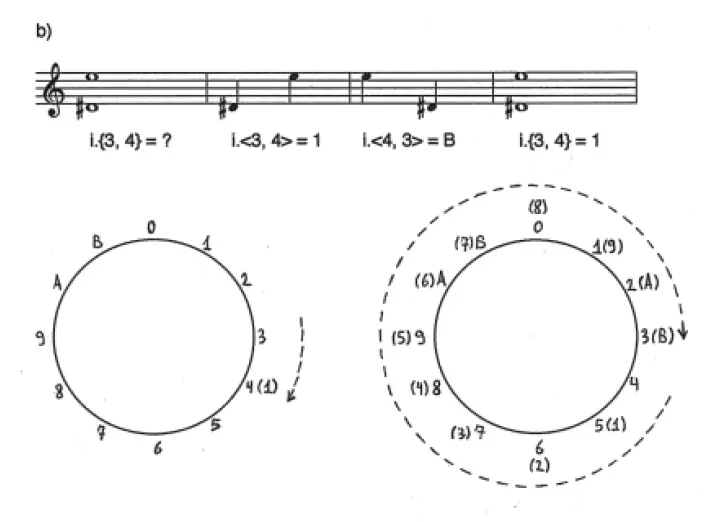
En el ejemplo 12 b) se lleva a cabo el mismo procedimiento con las c.a. 3 y 4. Se puede apreciar que la suma de cada par de intervalos pertenecientes a una misma c.i. siempre da como resultado 0 (mód. 12). En el caso del ejemplo 12 a), tenemos que 7 + 5 = 0 (mód. 12), mientras que en 12 b), 1 + B = 0 (mód. 12). Gráficamente, esto se traduce siempre en dos recorridos complementarios cuya unión es exactamente igual al recorrido total de la circunferencia del espacio-c.a. (véanse las gráficas de los ejemplos 12 a) y 12 b). La única c.i. cuyos dos intervalos expresan recorridos equidistantes en la circunferencia del espacio-c.a. es la c.i. 6, ya que 6 + 6 = 0 (mód. 12). Este caso se ilustra en el ejemplo 12 c).

En el ejemplo 13 se muestran las seis diferentes clases de intervalos que genera el espacio-c.a., acompañadas de los intervalos (ordenados) individuales que las conforman.

CLASES DE INTERVALOS CON INTERVALOS INDIVIDUALES INCLUIDOS

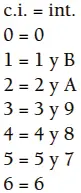
Es común en el pensamiento musical del siglo XX, concebir el material sonoro dentro de la dimensión del espacio-c.a. Como muestra de esto reconsideremos el pasaje presentado en el ejemplo 7.

APLICACIÓN LINEAL DE INTERVALOS ORDENADOS Y NO ORDENADOS EN EL ESPACIO-A Y C.A.

La perspectiva interválica ofrecida por el espacio-c.a. nos revela la existencia de una simetría estructural subyacente. Se trata de un palíndroma, similar al analizado anteriormente en el ejemplo 6. En el caso del ejemplo 14, el eje de simetría está representado por el intervalo 4 y la clase de intervalo 4 que separan a la última nota del primer sistema de la primera nota del segundo. Se puede apreciar que los intervalos y clases de intervalos ubicados en posiciones equidistantes a ambos lados de dicho eje coinciden:

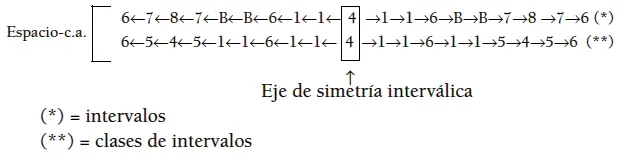
En el ejemplo 14, esta estructura palindrómica pasa totalmente inadvertida en el análisis interválico del espacio-a, debido a que es obstaculizada por la intervención del parámetro de registro (inactivo en el espacio-c.a.). Esto no quiere decir que las herramientas interválicas del espacio-a sean menos poderosas o precisas que las del espacio-c.a. Como ejemplo de lo contrario, basta con revisar el ejemplo 6, en el cual dichas herramientas revelaron perfectamente el diseño estructural subyacente. Se trata más bien de herramientas diferentes, altamente especializadas, que adquieren relevancia en la medida en que el espacio dentro del cual se desenvuelve el discurso musical las ratifique. Si en el pasaje del ejemplo 14 se buscara establecer una comparación estadística entre los intervalos simples y compuestos, o definir aspectos del contorno melódico, tales como la ubicación de los puntos climáticos interválicos o de registro, entonces la información interválica del espacio-a sería el vehículo adecuado.