Hebert Vázquez - Fundamentos teóricos de la música atonal

La segunda congruencia involucra tanto al proceso acumulativo de la mano derecha del pianista, como a la tendencia hacia el agregado del piano y su obtención final por parte del violín. Ya vimos (e ilustramos en el ejemplo 31) que el registro del piano alcanza una extensión máxima de 60, antes de que aparezca el violín, en el compás 8, para llevar a cabo el relevo instrumental en el despliegue del agregado. Pues bien, la misma extensión máxima de 60, asociada a una densidad máxima de cuatro notas por ataque, es alcanzada por la mano derecha en J3, precisamente en el momento en el que el violín completa el agregado, como se puede ver en el ejemplo 34. Esta coordinación entre el punto climático de la mano derecha y la obtención del agregado por parte del violín sugiere una atractiva hipótesis para explicar la permutación de los dos últimos elementos del agregado del violín, las alturas 16 y 26. Recordemos que el violín empieza desplegando el agregado en forma cromática ascendente, en dirección opuesta al piano, por lo que se esperaría que concluyera con la altura 26, precedida por la 16, tal como se muestra en el ejemplo 31. Sin embargo, el orden de estas últimas dos alturas se encuentra permutado en la partitura, lo que propicia una coincidencia exacta entre la nota más alta del agregado en el violín, la altura 26, y el primer ataque del acorde, también climático, de la mano derecha del pianista, representado por J3.

En el ejemplo 35 se presenta un diagrama del tipo de Euler-Venn que ayudará a visualizar la relación de inclusión entre conjuntos. La letra U representa al universo.

Diagrama de la relación de inclusión entre los conjuntosS yQ

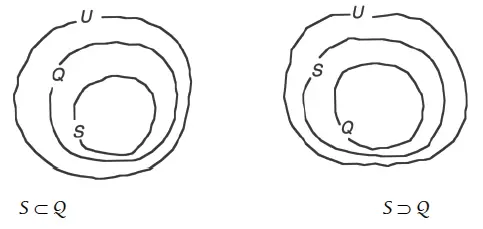
También se puede indicar la inclusión invirtiendo los términos, es decir, escribiendo S ⊃ Q, que significa “S contiene a Q” , como se puede ver en el diagrama anterior.

Si S y Q son dos conjuntos, entonces podemos tener un tercer conjunto S ∪ Q, al que llamaremos “la unión de S y Q ”, que es el conjunto más pequeño posible que contiene a S y Q como subconjuntos. Esto lo representamos como:

S ∪ Q = { x | x ∈ S v x ∈ Q }

Lo que significa que S ∪ Q es el conjunto cuyos elementos son aquellas x tales que x es uno de los elementos de S , o x es uno de los elementos de Q. En otras palabras, S ∪ Q es el conjunto que resulta de reunir en uno solo a los elementos de S y Q.

En el ejemplo 28 se abordó un pasaje de la sonata para piano de Armando Luna, que es reproducido ahora en el ejemplo 36. Viéndolo más detenidamente, se puede observar que el pasaje está basado en un gesto musical que involucra dos elementos: 1) un acorde de cinco notas que aparece en el primer tiempo de los compases 1 y 2, así como en el compás 3, y 2) un arpegio ascendente que se mueve por cuartas y que va incorporando elementos en cada una de sus apariciones (la primera vez que se escucha contiene las c.a. 0 y 6, mientras que en su segunda aparición contiene las c.a. 0, 6 y B). Si bien en el ejemplo sólo se muestran los primeros tres compases de la pieza, la tendencia acumulativa del arpegio es un elemento fundamental del discurso inicial de la obra.

En el ejemplo 36, el proceso acumulativo de los arpegios queda expresado en la relación K ⊂ L; mientras que la sonoridad total del fragmento, concebida como el producto de la reunión de dos procesos (conjuntos) independientes, queda expresada en la relación L ∪ J = X

RELACIÓN DE UNIÓN ENTRE CONJUNTOS DE CLASES DE ALTURAS (ARMANDO LUNA, SONATA PARA PIANO: 1ER MOV., DANZA, CC. 1-3)

El siguiente diagrama nos ayuda a visualizar la relación de unión entre conjuntos:

Diagrama de la relación de unión entre los conjuntos

[no image in epub file]

Si S y Q son dos conjuntos, entonces podemos tener un tercer conjunto que resulta de quedarse únicamente con los elementos que S y Q tienen en común. Este nuevo conjunto, al que llamaremos S ∩ Q, denota la intersección entre ambos.

Podemos representar la definición anterior por medio de la siguiente proposición:

S ∩ Q = { x | x ∈ S ∧ x ∈ Q }

Lo que significa que S ∩ Q es el conjunto cuyos elementos son aquellas x tales que x es elemento de S y x es elemento de Q.

En el ejemplo 38 tenemos un pasaje de Chain 2, para violín y orquesta, de Lutoslawski, en el que solamente participan el instrumento solista y la sección de cuerdas.

RELACIÓN DE INTERSECCIÓN ENTRE CONJUNTOS DE CLASES DE ALTURAS (WITOLD LUTOSLAWSKI, CHAIN 2, PARA VIOLÍN Y ORQUESTA: 4. A BATTUTA, Nº DE ENSAYO 116-117)

El conjunto V = {1,2,3,8,9,A,B} representa las c.a. empleadas por el violín en el pasaje, mientras que el conjunto S = {0,4,6,7,8} corresponde a las c.a. de la sección de cuerdas. La intersección entre ambos conjuntos aparece representada por el conjunto V ∩ S = {8}, ya que ésta es la única c.a. que comparten.

Se puede observar que la c.a. 8 juega un papel muy particular dentro del fragmento, ya que se escucha dos veces dentro del primer grupo de dieciseisavos en la parte del violín, mientras que en la sección de cuerdas es diferida hasta la entrada de los contrabajos; sin embargo, una vez que es incorporada al conjunto de la sección de cuerdas, desaparece de la parte del solista y es sustituida por la c.a. 1, que hace su aparición en el segundo grupo de dieciseisavos (en la parte del violín). De esta forma, la intersección entre los dos conjuntos es utilizada para llevar a cabo una transferencia de material entre el solista y la sección de cuerdas.

La relación de intersección entre conjuntos se ejemplifica en el siguiente diagrama:

Diagrama de la relación de intersección entre los conjuntos S y Q

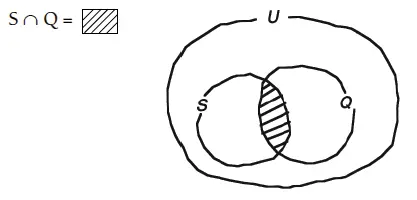
Si S y Q son dos conjuntos, y S ∩ Q = ∅, entonces se dice que los conjuntos S y Q son ajenos o disjuntos, ya que no tienen ningún elemento en común.

En el ejemplo 40, la relación de conjuntos ajenos enfatiza el contraste entre el discurso dinámico del instrumento solista, localizado en un primer plano, y la desintegración rítmica de la sección de cuerdas, que es empleada como textura de fondo.