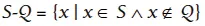Hebert Vázquez - Fundamentos teóricos de la música atonal

RELACIÓN DE CONJUNTOS AJENOS ENTRE CONJUNTOS DE CLASES DE ALTURAS (WITOLD LUTOSLAWSKI, CHAIN 2, PARA VIOLÍN Y ORQUESTA: 1. AD LIBITUM, Nº DE ENSAYO 2-3)

El conjunto del violín es: V = {0,1,3,4,5,8,B}, mientras que el correspondiente a la sección de cuerdas, que actúa en el pasaje sin los violines primeros, es S = {2,6,9,A}. Obsérvese que V ∩ S = ∅, ya que estos dos conjuntos no comparten ninguna c.a.

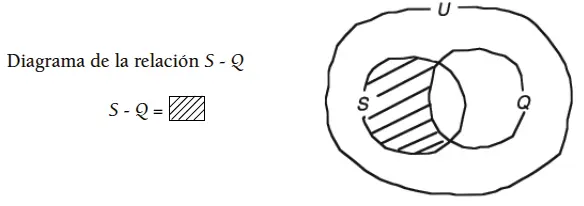
Diagrama de la relación de conjuntos ajenos entre S y Q

Si S y Q son dos conjuntos, entonces podemos tener un tercer conjunto que denotaremos con el símbolo S - Q, que leeremos “S menos Q” o “complemento de Q relativo al conjunto S” , que se caracteriza por ser el subconjunto más grande de S que es ajeno a Q :

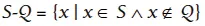
En el ejemplo 38 se representó con el conjunto V = {1,2,3,8,9,A,B} el material del violín solista y con S = {0,4,6,7,8} el de la sección de cuerdas, por lo que S - V = {0,4,6,7}. Este último contiene todas las clases de alturas de los instrumentos de la sección de cuerdas que inician a principio de compás, quedando excluida la c.a. 8 que aparece posteriormente en los contrabajos (ver ejemplo 38).

Si S y Q son dos conjuntos, entonces Q será el complemento de S si contiene todos los elementos del universo que no aparecen en el conjunto S . El complemento de un conjunto se indica normalmente trazando una línea horizontal sobre la letra que lo representa. Así, S será el complemento del conjunto S y viceversa:

S = { x I x ∉ S ∧ x ∈ U }

Observemos que U - S = S, por lo que S ∪ S =U, mientras que S ∩ S = ∅.

CONJUNTOS DE C.A. COMPLEMENTARIOS (WITOLD LUTOSLAWSKI, CHAIN 2, PARA VIOLÍN Y ORQUESTA: 1. AD LIBITUM, Nº DE ENSAYO 15-16)

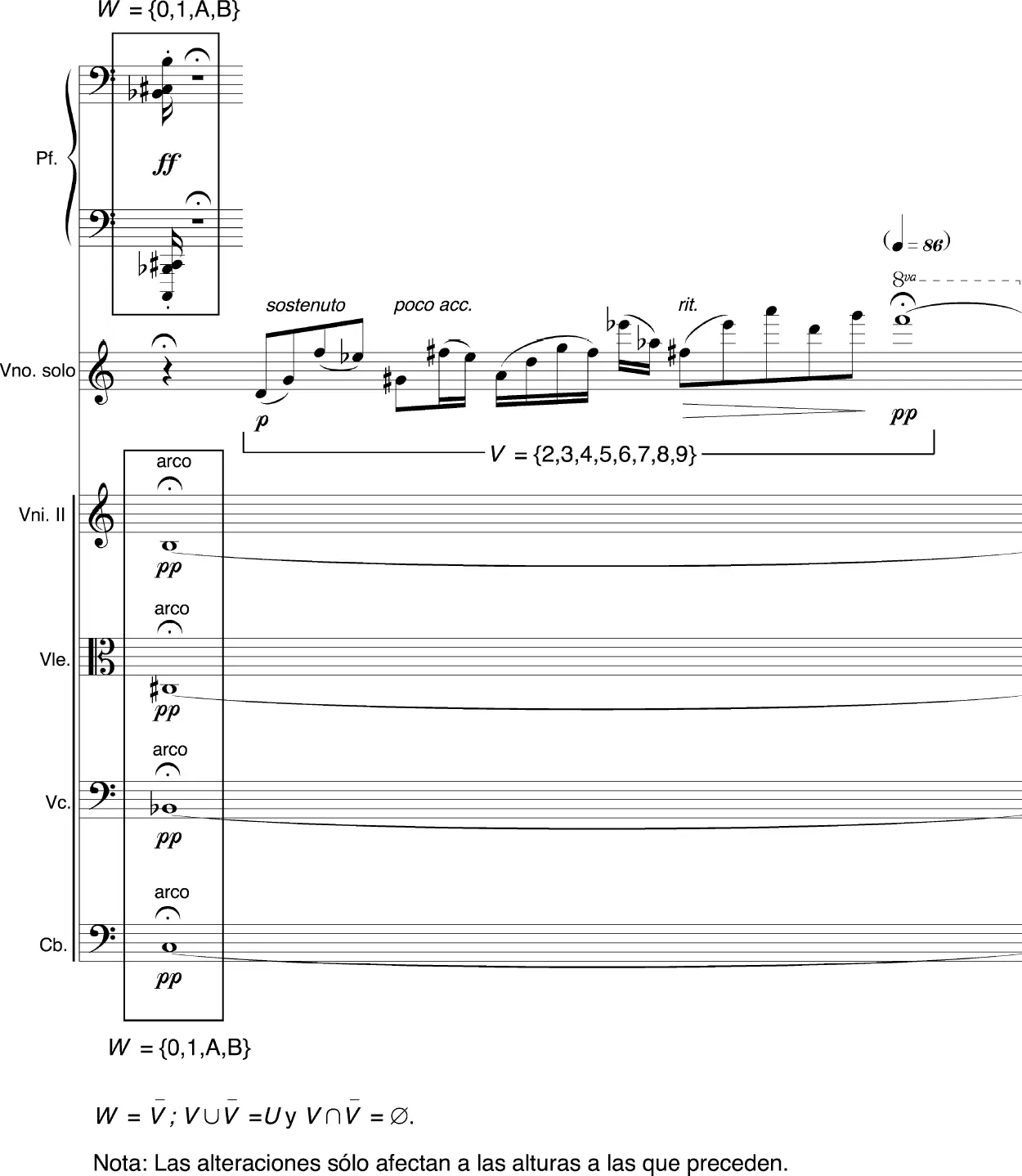
En el ejemplo 43, el conjunto V = {2,3,4,5,6,7,8,9} contiene las c.a. utilizadas por el violín solista, mientras que el conjunto W = {0,1,A,B} contiene las c.a. utilizadas tanto por el piano como por la sección de cuerdas (sin violines primeros). Obsérvese que el conjunto W = V, ya que contiene todas las c.a. del universo que no se encuentran en V , además de no compartir ninguna c.a. con dicho conjunto.

No olvidemos que nos encontramos en el espacio-c.a., por lo que U = agregado = V ∪ V.

El ejemplo 44 presenta otro caso de conjuntos complementarios.

EL COMPLEMENTO DE LA UNIÓN DE DOS CONJUNTOS (ARMANDO LUNA, SONATA PARA PIANO: 1ER MOV., DANZA. CC. 21-32)

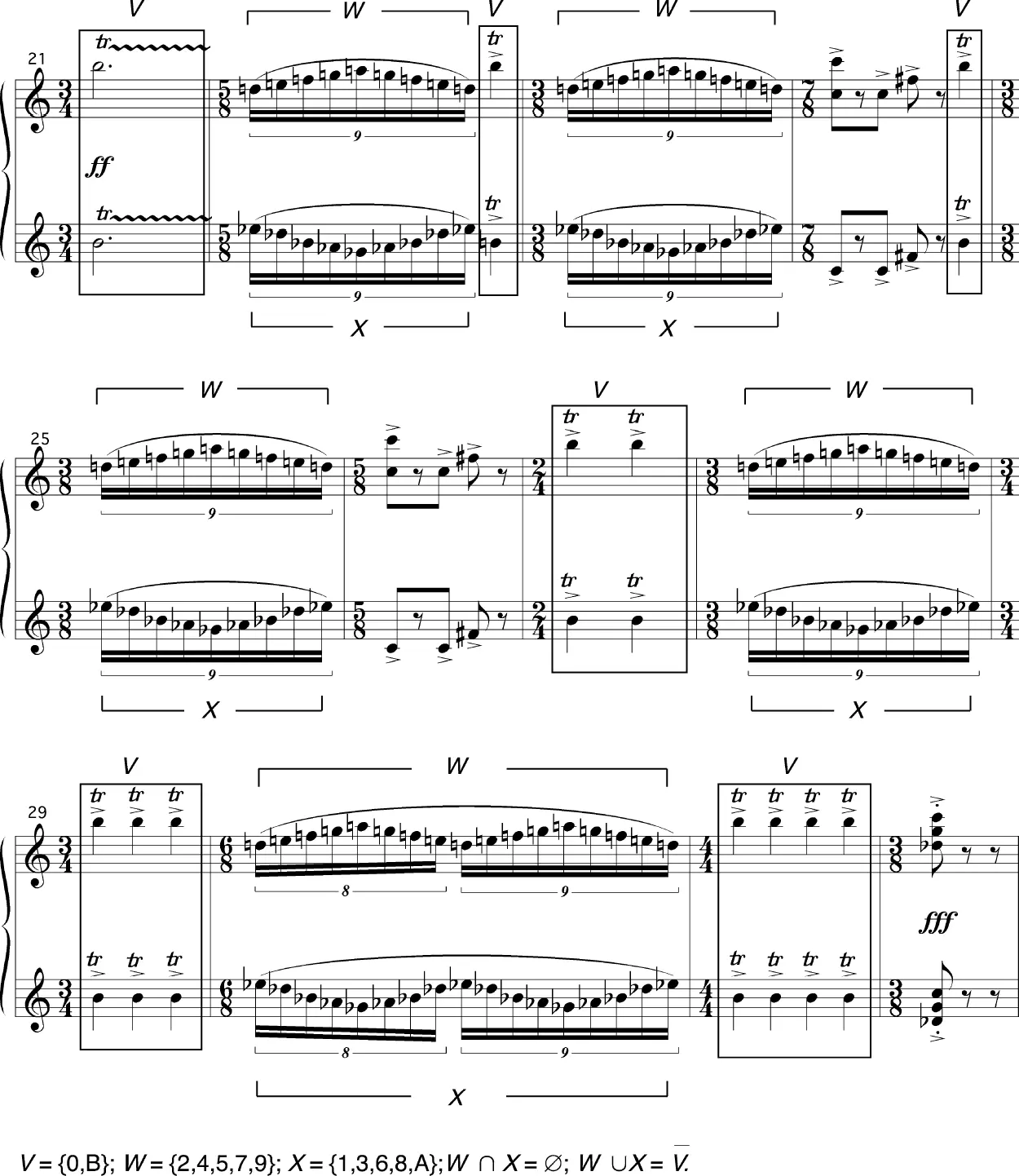
El conjunto V = {0,B} del compás 21 representa, desde la perspectiva del registro, el punto climático de un pasaje previo de contorno ascendente, no incluido en el ejemplo. Se puede apreciar que la influencia de V como punto climático se mantiene a lo largo de todo el pasaje, y que su actividad rítmica se ve incrementada paulatinamente hasta el momento en que finalmente desemboca en el acorde del compás 32.16 El conjunto V interactúa con otros dos objetos sonoros a lo largo del fragmento (sin contar el acorde final del compás 32); éstos son: los nonillos con valor de dieciseisavo, representados por el conjunto W en la mano derecha y X en la mano izquierda, y el conjunto formado por las c.a. 0 y 6, que aparecen a principio del compás 24 y en el compás 26. Dejando a un lado este último conjunto, así como el acorde final del pasaje, que serán discutidos en el capítulo 4 (punto 4.1), tenemos que los conjuntos W = {2,4,5,7,9} y X = {1,3,6,8,A} son conjuntos ajenos, ya que W ∩ X = ∅. Debido a que W y X aparecen siempre en forma simultánea, además de que tienen la misma duración y comparten un contorno simétrico invertido, dicho par de conjuntos son percibidos auditivamente como una sola sonoridad, a la que llamaremos conjunto Y , que se define por la relación W ∪ X = Y = {1,2,3,4,5,6,7,8,9,A}. Podemos observar también que V = Y , y viceversa, ya que V ∩ Y = ∅ y V ∪ Y = U dentro del contexto del espacio-c.a. La relación de complementos mutuos entre V e Y se encuentra resaltada en la partitura por la cercanía que ambos conjuntos mantienen durante todo el pasaje.

Diagrama de conjuntos complementarios

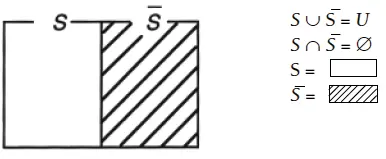
Ya se comentó que no importa la cardinalidad de cada conjunto, por lo que S ≤ S, ó S > S.

Esta relación entre conjuntos se define en función de la unión, intersección y diferencia relativa. Si S y Q son dos conjuntos, entonces S ∆ Q = ( S ∪ Q )- ( S ∩ Q ).

La diferencia simétrica indica que S ∆ Q es el conjunto formado por los elementos que pertenecen a S o a Q , pero no a ambos (es decir, los elementos de S y Q que quedan fuera de la intersección entre ambos conjuntos).

El pasaje musical del ejemplo 46 hace un uso extenso de la diferencia simétrica.

DIFERENCIA SIMÉTRICA ENTRE CONJUNTOS DE C.A. (HEBERT VÁZQUEZ, LAS NOSTÁLGICAS MUTACIONES DEL NÚCLEO, PARA GUITARRA AMPLIFICADA Y ORQUESTA: CC. 260-266)

Los conjuntos en los que están organizadas las clases de alturas del fragmento son α = {0,2,3,5,6,8,9,B}, β = {0,1,3,4,6,7,9,A}, y γ = {1,2,4,5,7,8,A,B}. Estos tres conjuntos de cardinalidad 8 poseen la misma estructura interválica, basada en la alternancia de intervalos 1 y 2 entre elementos contiguos. A este tipo de conjuntos se le conoce con el término genérico de colección octáfona y únicamente existen tres ejemplares diferentes de ellos, justamente los que hemos denominado α, β y γ. Un aspecto interesante de los tres conjuntos octáfonos es que α Δ β = γ; α Δ γ = β; y β Δ γ = α. Esto quiere decir que la diferencia simétrica entre dos conjuntos octáfonos cualesquiera será siempre igual al tercer conjunto octáfono faltante, como podrá comprobar el lector.