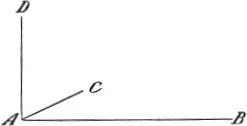Galileio Galilei - Dialog über die beiden hauptsächlichsten Weltsysteme

Simpl.Mittels der Geraden A F und nicht mittels der krummen Linie, da die krummen Linien zu solchem Zweck bereits als untauglich sich erwiesen haben.

Sagr.Was mich betrifft, so würde ich weder die eine noch die andere benutzen; denn, wie ich sehe, geht die Gerade A F in schiefer Richtung. Ich möchte vielmehr eine Linie ziehen, die rechtwinklig auf C D steht; denn diese und diese allein scheint mir die kürzeste zu sein im Gegensatz zu den unendlich vielen größeren und unter sich ungleichen, welche von dem Endpunkte A nach anderen und anderen Punkten der gegenüberliegenden Linie C D sich ziehen lassen.

Salv.Eure Wahl und der Grund, den Ihr dafür anführt, scheinen mir vortrefflich. Wir haben also bis jetzt das Ergebnis, dass die erste Dimension durch eine gerade Linie bestimmt wird; die zweite, nämlich die Breite, ebenfalls durch eine gerade Linie, die mit jener anderen, die Länge bestimmenden einen rechten Winkel bildet. So also haben wir die zwei Dimensionen der Fläche bestimmt, die Länge und Breite. Wenn Ihr nun aber eine Höhe zu bestimmen habt, wie hoch z. B. die Decke dieses Zimmers über dem Fußboden sich befindet, so kann man doch von einem beliebigen Punkte der Decke unendlich viele teils gerade, teils krumme Linien, alle von verschiedener Länge, nach unendlich vielen Punkten des darunter befindlichen Bodens ziehen. Welche von genannten Linien würdet Ihr nun zu Eurem Zwecke benutzen?

Sagr.Ich würde an der Decke einen Faden befestigen und ihn durch eine daran hängende Bleikugel sich ungehindert ausdehnen lassen, bis er den Boden berührt. Die Länge dieses Fadens, als einer geraden Linie und zwar der kürzesten von allen Linien, die von selbigem Punkte nach dem Boden sich ziehen lassen, würde ich als die wahre Höhe des Zimmers betrachten.

Salv.Ganz richtig. Wenn Ihr dann von dem Punkte des Fußbodens, der durch das Ende des hängenden Fadens bezeichnet ist – der Boden als waagrecht angenommen, nicht etwa als geneigt – zwei andere gerade Linien ausgehen lasset, eine in Richtung der Länge, die andere in Richtung der Breite des Bodens, welche Winkel werden diese mit dem Faden bilden?

Sagr.Sie werden selbstverständlich rechte Winkel bilden, wenn der Faden lotrecht und der Boden ganz eben und genau waagrecht ist.

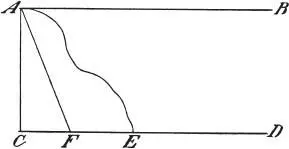
Salv.Wenn Ihr also irgendeinen Punkt zum Anfang und Ausgangspunkt der Messung macht und von ihm eine gerade Linie ausgehen lasst, die zur Bestimmung der ersten Ausdehnung, der Länge, dienen soll, so wird notwendigerweise diejenige, welche die Breite definieren soll, rechtwinklig zur ersten abgehen und die, welche die Höhe, also die dritte Ausdehnung, bezeichnet, ebenfalls mit den beiden anderen nicht schiefe, sondern rechte Winkel bilden. So seht Ihr denn durch die drei Perpendikel, als drei in ihrer Art einzige, bestimmte und kürzeste Linien, die drei Dimensionen festgesetzt: A B die Länge, A C die Breite, A D die Höhe. Da nun offenbar durch denselben Punkt keine weitere Linie gehen kann, welche mit diesen rechte Winkel einschließt und die Dimensionen doch allein durch gerade, aufeinander rechtwinklige Linien bestimmt werden dürfen, so gibt es nicht mehr als drei Dimensionen. Ein Ding also, das diese drei besitzt, besitzt sie alle, und wenn es alle besitzt, ist es nach allen Richtungen teilbar, und wenn dem so ist, ist es vollkommen u. s. w.

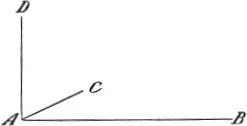
Simpl.So? Wer sagt denn, dass man keine anderen Linien ziehen kann? Warum sollte es denn unmöglich sein, von unten her noch eine weitere Linie im Punkte A anlangen zu lassen, die mit den übrigen rechte Winkel bildet?

Salv.Ihr könnt doch wahrhaftig nicht durch einen Punkt mehr als drei aufeinander rechtwinklige Linien legen.

Sagr.Ja; denn die, welche Signore Simplicio meint, scheint mir dieselbe Linie wie D A zu sein, nur nach unten verlängert. Auf diese Art könnte man noch zwei andere ziehen; es wären aber die nämlichen drei wie zuvor, nur mit dem Unterschiede, dass sie dann sich schnitten, während sie jetzt sich bloß berühren. Neue Dimensionen würde man aber dadurch nicht erhalten.

Bei naturwissenschaftlichen Beweisen ist mathematische Strenge nicht erforderlich.

Simpl.Ich will nicht sagen, dass dieser Euer Beweis der Strenge ermangele; wohl aber kann ich mit Aristoteles 14sagen, dass man in den Naturwissenschaften nicht immer Beweise von mathematischer Strenge zu suchen braucht.

Sagr.Allerdings vielleicht dann nicht, wenn sie unerreichbar ist; wenn sie hier aber möglich ist, warum nicht Gebrauch von ihr machen? Doch es wird gut sein, auf diese Einzelheit nicht noch mehr Worte zu verschwenden, weil meiner Meinung nach Signore Salviati dem Aristoteles und Euch ohne jeden Beweis zugegeben hätte, dass die Welt ein Körper sei und dass sie Vollkommenheit und zwar die höchste Vollkommenheit besitze, wie sie ja das höchste Werk Gottes ist.

Nach Aristoteles zwei einander entgegengesetzte Teile der Welt, ein himmlischer und ein elementarer.

Salv.So ist es in der Tat. Lassen wir also die allgemeinen Betrachtungen des Weltganzen und gehen wir über zu der Betrachtung seiner Teile, deren Aristoteles im ersten Abschnitt zwei sehr verschiedene, gewissermaßen einander entgegengesetzte annimmt, nämlich einen himmlischen und einen elementaren: jener unentstanden, unzerstörbar, unveränderlich, unbeeinflussbar; dieser beständigem Wechsel und fortwährender Änderung unterworfen. Diesen Unterschied schöpft er aus seinem Grundprinzipe, nämlich aus der Verschiedenheit der Ortsveränderungen. 15Seine Schlüsse sind dabei folgende:

Drei Arten der Ortsbewegung, geradlinige, kreisförmige und gemischte.

Geradlinige und kreisförmige Bewegungen einfach, weil längs einfacher Linien erfolgend.

Aus der sinnlichen Welt sozusagen heraustretend und in eine ideale sich versetzend, unternimmt er es, den Bauplan des Weltalls zu entwerfen und demgemäß zu erwägen, dass die Natur die Ursache der Bewegung ist 16, die Naturkörper mithin der Ortsveränderung fähig sind. Er erklärt sodann, dass die Bewegungen von dreierlei Art sind, nämlich kreisförmig, geradlinig oder aus diesen gemischt. Die beiden ersten Bewegungsarten nennt er einfach, weil von allen Linien der Kreis und die Gerade allein einfach sind. Hierauf definiert er, die bisherige Allgemeinheit bedeutend einschränkend, von den einfachen Bewegungen sei die erste die Kreisbewegung, d. h. dieu mdie Mitte stattfindende, die beiden anderen seien gerade nach oben und nach unten gerichtet, nämlich nach oben die von dem Mittelpunkt sich entfernende, nach unten die dem Mittelpunkt zustrebende. Daraus nun schließt er, dass notwendigerweise die einfachen Bewegungen mit diesen drei Arten erschöpft sind, dass es also nur Bewegungen nach der Mitte, von der Mitte und um die Mitte gebe. Dieses steht, wie er sagt, in schönem Einklange mit dem früher über den Körper Gesagten, der ganz wie die ihm zukommende Bewegung in dreierlei Hinsicht vollkommen sei. Nach Feststellung dieser Bewegungsarten fährt er fort und sagt: Da von den Naturkörpern einige einfach, andere aus diesen zusammengesetzt seien – und zwar nennt er einfache Körper solche, die von Natur einen Antrieb zur Bewegung haben, wie das Feuer und die Erde –, so müssen die einfachen Bewegungen den einfachen Körpern, die gemischten den zusammengesetzten Körpern zukommen, derart jedoch, dass die zusammengesetzten dem vorherrschenden Bestandteile folgen.