Galileio Galilei - Dialog über die beiden hauptsächlichsten Weltsysteme

Zwischen der Ruhe und irgendwelchem Grade der Geschwindigkeit liegen unendlich viele Grade geringerer Geschwindigkeit.

Sagr.Ich höre von dieser Ansicht mit großem Vergnügen, glaube aber, das wird in noch höherem Maße der Fall sein, wenn Ihr mir erst ein Bedenken beseitigt habt; ich begreife nämlich nicht recht, wieso notwendig ein beweglicher Körper, der aus dem Zustande der Ruhe in eine Bewegung eintritt, zu der ein natürlicher Hang ihm innewohnt, alle vorhergehenden Grade der Schnelligkeit durchmachen muß, deren es zwischen einem beliebig vorgeschriebenen Grade und dem Zustande der Ruhe unendlich viele gibt: als wenn die Natur der Masse des Jupiter nicht gleich nach ihrer Schöpfung die kreisförmige Bewegung nebst der betreffenden Geschwindigkeit hätte zuerteilen können.

Die Natur verleiht nicht unmittelbar einen bestimmten Grad von Geschwindigkeit, wiewohl sie es könnte.

Salv.Ich habe nicht gesagt und möchte mich nicht erdreisten zu sagen, dass es der Natur und Gott unmöglich wäre, jene Geschwindigkeit, von der Ihr sprecht, auch unmittelbar zu verleihen; wohl aber sage ich, dass die Natur de facto nicht so verfährt. Ein solcher Vorgang käme also auf eine Wirkung hinaus, wie sie außerhalb des natürlichen Verlaufs liegt, also auf ein Wunder.*

Sagr.Ihr glaubt also, ein Stein, der aus der Ruhelage in die ihm natürliche Bewegung nach dem Mittelpunkt der Erde eintritt, müsse durch alle Stufen der Langsamkeit hindurchgehen, die unterhalb einer beliebigen Stufe der Geschwindigkeit liegen?

Salv.Ich glaube es, ja ich bin dessen sicher und zwar mit solcher Zuversicht, dass ich auch Euch darüber völlig vergewissern kann.

Sagr.Wenn ich bei allen unseren heutigen Untersuchungen auch nur diese eine Erkenntnis gewänne, würde ich das als eine bedeutende Errungenschaft betrachten.

Der vom Ruhestand ausgehende Körper geht durch alle Stufen der Geschwindigkeit hindurch, ohne auf irgendeiner zu verweilen.

Salv.Soweit ich Euch verstanden zu haben glaube, richtet sich Euer Haupteinwurf gegen die Vorstellung, dass ein Körper durch jene unendlich vielen vorangehenden Stufen der Langsamkeit und noch dazu in kürzester Frist hindurchgehen soll, bis er die nach dieser Frist ihm zukommende Geschwindigkeit erreicht. Darum will ich, bevor ich weiter gehe, dieses Bedenken zu beseitigen suchen, was nicht schwer ist. Ich brauche Euch bloß zu entgegnen, dass der Körper zwar durch die genannten Stufen hindurchgeht, aber ohne bei diesem Durchgang auf irgendeiner Stufe zu verweilen. Da demnach der Durchgang nicht mehr als einen einzigen Augenblick erfordert, aber jede noch so kleine Frist unendlich viele Augenblicke enthält, so werden wir eine genügende Menge von Augenblicken zur Verfügung haben, um den unendlich vielen verschiedenen Stufen der Langsamkeit je einen bestimmten Zeitpunkt zuzuordnen, mag die Frist auch noch so klein sein.

Sagr.Soweit folge ich; gleichwohl kommt es mir auffällig vor, wenn eine Kanonenkugel, – als solche will ich mir den fallenden Körper vorstellen –, die doch mit solchem Ungestüm niederfällt, dass sie in weniger als zehn Pulsschlägen mehr als zweihundert Ellen 26zurücklegt, im Laufe ihrer Bewegung einen so geringen Grad von Geschwindigkeit soll besessen haben, dass, wenn sie diesen beibehalten und keine weitere Beschleunigung erfahren hätte, sie die Strecke nicht in einem ganzen Tage zurückgelegt haben würde.

Salv.Ihr dürft ruhig sagen, in einem ganzen Jahre nicht, noch auch in zehn oder in tausend Jahren. Ich verbürge mich, Euch davon zu überzeugen, ohne dass Ihr vielleicht gegen eine der einfachen Fragen Einspruch erhebt, die ich an Euch richten werde. Sagt mir also, ob Ihr ohne Weiteres zugebt, dass jene Kugel beim Fallen immer größeren Antrieb und Geschwindigkeit erlangt.

Sagr.Dessen bin ich völlig gewiss.

Salv.Und wenn ich behaupte, dass der an irgendeiner Stelle erreichte Antrieb der Bewegung gerade groß genug ist, um die Kugel wieder zu der Höhe zurückzubringen, von der sie ausging, werdet Ihr mir Recht geben?

Der schwere Körper erlangt beim Fall einen Antrieb, der ausreichend ist, um ihn wieder auf dieselbe Höhe zu bringen.

Sagr.Unbedingt, sobald sie ungehindert ihre volle Kraft für den einen Zweck verwenden kann, um selbst wieder zur früheren Höhe zu gelangen oder um einen anderen ihr gleichen Körper dahin zu bringen. Wäre z. B. die Erde durch den Mittelpunkt hindurch durchbohrt und ließe man die Kugel aus einer Höhe von hundert oder tausend Ellen fallen, so bin ich überzeugt, dass sie jenseits des Mittelpunktes sich ebenso weit über diesen erhöbe, als sie zuvor gefallen ist. Eben dasselbe ist der Fall, wie der Versuch mich lehrt, bei einem an einem Faden aufgehängten Gewichte. Entfernt man dieses aus der Ruhelage, also der lotrechten Richtung, und überlässt es sich selbst, so fällt es in die lotrechte Lage zurück und überschreitet sie um ebenso viel oder doch nur um soviel weniger, als der Widerstand der Luft und des Fadens oder anderer Nebenumstände dies bewirken. Auch beim Wasser, welches in eine Röhre gegossen ebenso weit steigt, als die Höhe seines Falls betrug, zeigt sich mir das nämliche. 27

Salv.Eure Schlüsse sind untadelig. Ihr werdet auch sicherlich damit einverstanden sein, dass die Ursache des erlangten Antriebes die wachsende Entfernung des Körpers vom Ausgangspunkte und die Annäherung an den bei der Bewegung erstrebten Mittelpunkt ist. Werden aber auch zwei gleiche Körper, wenn sie, ohne Widerstand zu finden, längs verschiedener Linien sich abwärts bewegen, dennoch gleiche Antriebe erlangen, die Annäherung an den Mittelpunkt in beiden Fällen als gleich vorausgesetzt? Räumt Ihr das gleichfalls ein?

Sagr.Ich verstehe die Frage nicht recht.

Salv.Ich werde mich besser mit Hilfe einer kleinen Zeichnung verständlich machen. Ich ziehe also diese Linie A B in horizontaler Richtung, errichte im Punkte B die Senkrechte C B und ziehe dann die schiefe Verbindungslinie C A . Wenn ich mir nun unter der Linie C A eine geneigte Ebene von ausgezeichneter Glätte und Härte vorstelle, auf welcher eine vollkommen runde Kugel von härtestem Stoff sich abwärts bewegt; wenn ferner eine zweite derartige Kugel längs der Senkrechten C B in freiem Falle sich bewegt, so frage ich: Räumt Ihr ein, dass der Antrieb der Kugel, welche längs der geneigten Ebene fällt, nach Ankunft in A gleich dem Antriebe sein kann, welche die andere im Punkte B erlangt, nachdem sie die lotrechte Strecke C B passiert hat?

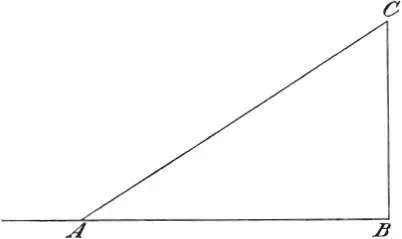
Die Antriebe zweier Körper, die sich gleichviel dem Mittelpunkt genähert haben, sind gleich.

Sagr.Ich glaube bestimmt: ja. Denn schließlich haben sich beide dem Mittelpunkt gleichviel genähert und nach dem, was ich soeben eingeräumt habe, würde der Antrieb einer jeden von beiden genügen, um sich selbst wieder zu gleicher Höhe zu erheben.

Salv.Sagt mir nun noch, wie sich Eurer Ansicht nach die nämliche Kugel verhielte, wenn man sie auf die waagrechte Ebene A B legen würde?

Auf der waagrechten Ebene bleibt der Körper ruhig liegen.

Sagr.Sie würde ruhig liegen bleiben, da die Ebene nach keiner Seite geneigt ist.

Salv.Auf der geneigten Ebene C A hingegen würde sie sich abwärts bewegen, aber langsamer als längs der Senkrechten C B , nicht wahr?