Galileio Galilei - Dialog über die beiden hauptsächlichsten Weltsysteme

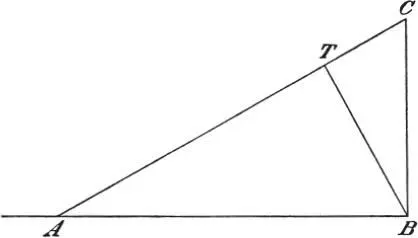
Sagr.Mein größtes Bedenken ist jetzt gehoben und ich begreife nicht bloß die Möglichkeit, sondern geradezu die Notwendigkeit dessen, was mir vorher ein Widerspruch schien. Ich verstehe aber einstweilen noch nicht, dass zu diesen möglichen oder notwendigen Fällen der hier vorliegende gehört. Es müsste sich herausstellen, dass die Fallzeit längs C A zur Zeit des freien Falls längs C B sich ebenso verhält wie die Linie C A zu C B , damit man ohne Widerspruch soll sagen können, die Geschwindigkeiten längs der schiefen Linie C A und längs der senkrechten C B seien gleich.

Salv.Seid einstweilen zufrieden, dass ich Euch den Unglauben benommen habe; die volle Erkenntnis erwartet ein anderes Mal, wenn Euch die Untersuchungen unseres Akademikers über die räumlichen Bewegungen vorliegen. 30Ihr werdet dort bewiesen finden, dass, wenn der eine Körper die ganze Linie C B durchfallen hat, der andere am Fußpunkte T des von B auf C A gefällten Perpendikels angelangt ist. Um andererseits den Ort des nämlichen senkrecht fallenden Körpers zu finden in dem Augenblicke, wo der andere in A ankommt, errichtet bloß im Punkte A ein Perpendikel auf C A und verlängert es bis zum Schnitt mit C B ; dort wird der gesuchte Punkt liegen. Inzwischen werdet Ihr bemerken, dass es völlig richtig ist, die Bewegung längs C B als rascher zu betrachten wie die längs der schiefen Linie C A – die zu vergleichenden Bewegungen immer vom Ausgangspunkte C an gerechnet –, denn die Linie C B ist größer als C T , und ebenso ist die Linie von C bis zum Schnitt mit dem im Punkte A auf C A errichteten Perpendikel größer als C A : Darum ist also die Bewegung auf jener rascher als längs C A . Vergleichen wir aber die über die ganze Linie C A erstreckte Bewegung nicht mit der ganzen gleichzeitig stattfindenden Bewegung längs der verlängerten Senkrechten, sondern bloß mit dem schon in kürzerer Zeit zurückgelegten Teile C B , so ist es sehr wohl angängig, dass der längs C A über T hinaus weiter fallende Körper nach einer solchen Frist in A ankommt, dass, wie C A zu C B , so auch die eine Zeit zur anderen sich verhält.

Die Kreisbewegung kann niemals auf natürliche Weise ohne vorangehende geradlinige Bewegung zustande kommen.

Kreisbewegung ist in Ewigkeit gleichförmig.

Die Größe der Bahnen und die Geschwindigkeit der Planetenbewegung haben dasjenige Verhältnis, welches einer Abwärtsbewegung von gemeinsamem Ausgangspunkt entspricht.

Wir wollen nun wieder unser erstes Ziel ins Auge fassen und beweisen, dass ein schwerer Körper, der von der Ruhelage ausgeht, bei seinem Falle durch alle die Stufen der Langsamkeit hindurchgehen muss, welche einer später von ihm erreichten Stufe der Geschwindigkeit vorangehen. Wir nehmen dieselbe Figur wiederum vor und erinnern uns, dass nach beiderseitigem Zugeständnis der senkrecht längs C B fallende Körper und der schief längs C A fallende in den Endpunkten B und A mit gleichen Stufen der Geschwindigkeit eintreffen. Wir gehen nun weiter, und ich glaube, Ihr werdet ohne jedes Bedenken zugeben, dass auf einer Ebene, die weniger steil ist als A C , etwa auf A D , die Abwärtsbewegung noch langsamer als auf der Ebene A C stattfinden wird. Daher lassen sich, wie nicht im Mindesten zu bezweifeln ist, Ebenen von so geringer Neigung gegen den Horizont angeben, dass der bewegte Körper, also die von Anfang an betrachtete Kanonenkugel, erst nach einer vorgegebenen beliebig großen Zeit den Weg bis zum Endpunkte A zurücklegen würde. Um nämlich längs B A dorthin zu kommen, reicht auch unendliche Zeit nicht aus, und die Bewegung wird umso langsamer, je geringer die Steilheit ist. Man muss also unbedingt zugeben, es lasse sich über dem Punkte B ein Punkt in solcher Nähe annehmen, dass die durch ihn und den Punkt A gelegte Ebene von der Kugel auch nicht in einem Jahre zurückgelegt würde. – Nun müsst Ihr noch Folgendes wissen. Der Antrieb, mithin der Grad der Geschwindigkeit, welchen die Kugel bei ihrem Eintreffen im Punkte A erreicht hat, ist ein solcher, dass, wenn sie von nun ab mit diesem Grade von Geschwindigkeit sich weiter bewegte, d. h. ohne eine Beschleunigung oder eine Verzögerung zu erfahren, sie die doppelte Länge dieser Ebene in einer Zeit zurücklegen würde, die gleich ist der auf der schiefen Ebene verbrachten. 30) Wenn nämlich die Kugel etwa in einer Stunde die Ebene passiert hätte und sodann mit dem im Endpunkte A erreichten Grad von Geschwindigkeit fortführe sich zu bewegen, so würde sie in einer weiteren Stunde eine Strecke zurücklegen gleich dem doppelten von D A . Nun sind aber, wie wir festgestellt haben, die von den Körpern in B und A erreichten Geschwindigkeitsgrade stets gleich, vorausgesetzt, dass diese von einem beliebigen auf C B angenommenen Punkte ausgehen und sich abwärts bewegen, der eine längs der schiefen Ebene, der andere längs der Senkrechten. Der senkrecht fallende Körper kann also von einem so nahe bei B gelegenen Punkte ausgehen, dass die in B erreichte Geschwindigkeitsstufe nicht ausreichend wäre – wenn sie von nun an beibehalten würde –, um den Körper über eine Strecke von der doppelten Länge der schiefen Ebene in einem Zeitraume von einem Jahre oder von zehn oder von hundert Jahren zu befördern. Wir können also folgendermaßen schließen: Wenn wirklich im gewöhnlichen Laufe der Natur ein Körper nach Entfernung aller äußeren und zufälligen Hindernisse sich auf einer schiefen Ebene mit umso größerer Langsamkeit bewegt, je geringer die Schiefe ist, so dass schließlich die Langsamkeit unendlich groß wird, sobald nämlich die Schiefe aufhört und die Ebene in eine waagrechte Ebene übergeht, und wenn wirklich die in irgendeinem Punkte der schiefen Ebene erreichte Geschwindigkeitsstufe gleich ist der Geschwindigkeitsstufe, die der senkrecht fallende Körper an einer ebenso hochgelegenen Stelle erreicht, so muss man auch notwendig unserer Behauptung beistimmen, dass der von der Ruhelage aus fallende Körper durch alle die unendlich vielen Stufen der Langsamkeit hindurchgehen und folglich, um einen bestimmten Grad von Geschwindigkeit zu erlangen, sich zuerst in gerader Linie bewegen muss, 31und zwar eine kürzere oder längere Strecke, je nachdem die zu erreichende Geschwindigkeit kleiner oder größer sein soll und je nachdem die Ebene, auf der er sich abwärts bewegt, weniger oder mehr geneigt ist. Es lässt sich also auch eine Ebene mit so geringer Neigung angeben, dass der Körper, um auf ihr den vorgeschriebenen Grad von Geschwindigkeit zu erlangen, längs einer außerordentlich großen Strecke und während einer außerordentlich langen Zeit sich bewegt haben muss; auf der waagrechten Ebene wird er also von Natur aus niemals auch nur die geringste Geschwindigkeit erlangen, da er sich auf ihr ja überhaupt nicht bewegen wird. Die Bewegung längs der horizontalen Linie, die keine Schiefe oder Steilheit besitzt, ist aber nichts Anderes als die Kreisbewegung um den Mittelpunkt. Darum wird also die Kreisbewegung niemals ohne vorangehende geradlinige Bewegung zustande kommen; ist sie aber einmal zustande gekommen, so wird sie in Ewigkeit mit gleichförmiger Geschwindigkeit fortdauern. 32Ich könnte Euch diese nämlichen Wahrheiten noch durch andere Erwägungen erläutern und sogar beweisen; aber ich möchte nicht so weit von unserem Hauptgegenstande abschweifen und lieber bei einer anderen Gelegenheit darauf zurückkommen, umso mehr als wir jetzt auf dieses Thema nicht gekommen sind zum Zwecke eines strengen Beweises, sondern nur um einen Gedanken Platos 23weiter auszuführen. – Ich will daran noch eine eigentümliche Beobachtung unseres Akademikers reihen, die ans Wunderbare grenzt. Stellen wir uns vor, der göttliche Baumeister habe neben anderen Entwürfen den Plan gehegt, im Weltall jene Kugeln zu schaffen, die wir beständig im Kreise sich drehen sehen; er habe den Mittelpunkt ihres Kreislaufs bestimmt und in diesen unbeweglich die Sonne versetzt, habe dann alle die genannten Kugeln am nämlichen Orte verfertigt und ihnen den Trieb eingepflanzt, von hier aus sich abwärts nach dem Mittelpunkte hin zu bewegen, bis sie den Grad von Geschwindigkeit erlangt hätten, der dem göttlichen Geiste gut schien; als sie diesen erlangt, seien sie sodann in Drehung versetzt worden, jeglicher in seinem Kreise die zugewiesene Geschwindigkeit bewahrend. Es fragt sich nun, in welcher Höhe und welcher Entfernung von der Sonne der Ort gewesen ist, wo zu Anfang jene Kugeln geschaffen wurden, und ob möglicherweise die Schöpfung von allen an einem Orte stattgefunden hat. Zur Lösung dieser Frage hat man nach den Angaben der sachverständigsten Astronomen die Größe der Kreise zu Grunde zu legen, in welchen die Planeten umlaufen, sowie die Dauer dieser Umläufe. Aus diesen beiden gegebenen Größen berechnet man, wieviel mal schneller z. B. die Bewegung des Jupiters als die des Saturn ist. Findet man dann, wie es tatsächlich der Fall ist, dass Jupiter sich schneller bewegt, so muss, da beide von gleicher Höhe ausgegangen sind, Jupiter tiefer gefallen sein als Saturn, wie es denn bekanntlich auch wirklich sich verhält, da ja seine Bahn innerhalb der Saturnbahn liegt. Geht man aber weiter, so kann man aus dem Verhältnis der Geschwindigkeiten des Jupiters und Saturns, aus dem Abstand ihrer Bahnen und aus dem Maße der Beschleunigung bei der natürlichen Bewegung, wieder auffinden, in welcher Höhe und Entfernung vom Mittelpunkte ihrer Umdrehungen der Ort sich befunden hat, von dem sie ausgingen. Ist dieser aufgefunden und festgelegt, so fragt es sich, ob bei Mars, wenn er gleichfalls von dort bis zu seiner jetzigen Bahn hinabgestiegen ist, die Größe der Bahn und seine Geschwindigkeit mit dem durch Rechnung gefundenen Ergebnis stimmt; ähnlich steht es mit der Erde, mit Venus und mit Merkur, bei welchen die Größe der Kreise und die Geschwindigkeiten der Bewegung so nahe mit dem Resultate der Rechnung übereinstimmen, dass man sich nicht genug darüber wundern kann.