Galileio Galilei - Dialog über die beiden hauptsächlichsten Weltsysteme

Aristotelische Beweise dafür, dass es nicht mehr als drei Ausdehnungen gibt.

Berühmtheit der Dreizahl bei den Pythagoreern.

Simpl.Was habt Ihr denn an den wunderschönen Beweisen auszusetzen, die im zweiten, dritten und vierten Paragraphen gleich auf die Definition der Stetigkeit folgen? 9Steht da nicht erstlich, dass es keine anderen als jene drei Ausdehnungen gibt, weil die Drei alles, die Dreiheit allseitig ist? 10Wird dies nicht durch die Autorität und die Lehre der Pythagoreer bekräftigt, wonach alles durch die Drei, nämlich durch Anfang, Mitte und Ende bestimmt ist, diese also anzusehen ist als die Zahl der Allheit? Und vergesst Ihr denn ganz den weiteren Grund, dass nämlich gewissermaßen nach einem Naturgesetz besagte Zahl bei den Opfern für die Götter Anwendung findet, dass man, der Weisung der Natur vollkommen entsprechend, bei Dingen, die in der Dreizahl vorkommen, nicht aber bei einer geringeren Zahl, vona l l e nspricht? Denn wenn es sich um zwei Dinge handelt, sagt manb e i d eund nichta l l e ;wohl aber sagt man so bei dreien. Diese ganze Entwicklung findet Ihr im zweiten Paragraphen. Im dritten liest man ad pleniorem scientiam 10, dass die BegriffeJ e d e s ,A l lundV o l l k o m m e n e sbegrifflich identisch sind, dass also von den ausgedehnten Größen der Körper allein vollkommen ist, da nur er durch die Drei bestimmt ist, welche der Ausdruck der Allheit ist. Da er ferner in dreierlei Richtung geteilt werden kann, so ist er in allen Richtungen teilbar, während von den beiden anderen Größen die eine bloß auf eine, die andere auf zwei Weisen teilbar ist. Es entspricht nämlich die Teilbarkeit und Stetigkeit der Zahl der Dimensionen; daher ist die Linie nur in einer Richtung, die Fläche in zweien stetig, der Körper hingegen in allen. Gibt er sodann für die in Rede stehende Behauptung im vierten Paragraphen, nach einigen anderen Lehrsätzen, nicht noch einen weiteren Grund an? Jeder Fortschritt, sagt er, hat einen bisher vorhandenen Mangel zur Voraussetzung – und daher ist es ein Fortschritt, wenn man von der Linie zur Fläche übergeht, da jene der Breite ermangelt –, das Vollkommene kann aber nicht mangelhaft sein, da es allseitig ist; man kann also unmöglich von den Körpern zu einem höheren Gebilde fortschreiten. Scheint Euch nun nicht von all diesen Gesichtspunkten aus zur Genüge erwiesen, dass es über die drei Ausdehnungen der Länge, Breite und Tiefe hinaus einen Übergang zu einer weiteren nicht gibt und dass darum der Körper, der sie sämtlich besitzt, vollkommen ist?

Salv.Bei all diesen Erörterungen habe ich mich, offen gesagt, höchstens zu dem einen Zugeständnis bewogen gefühlt, dass dasjenige, was Anfang, Mitte und Ende hat, vollkommen zu nennen ist. Dass aber darum, weil Anfang, Mitte und Ende eine Dreiheit bilden, die Zahl Drei vollkommen wäre und die Fähigkeit besäße, diese Vollkommenheit auf jede Dreiheit von Dingen zu übertragen, dies zuzugeben fühle ich mich nicht im Mindesten bewogen. Ich kann z. B. nicht fassen und verstehen, dass etwa in Ansehung der Beine die Zahl Drei vollkommener wäre als Vier oder Zwei, oder dass die Zahl Vier als Zahl der Elemente unvollkommen sei, der Drei hingegen eine höhere Vollkommenheit zukäme. Besser wäre es also, man überließe derlei Nichtigkeiten Schönrednern und begründete seine Behauptung mit einem strengen Beweise, wie es sich in den deduktiven Wissenschaften gehört.

Simpl.Ihr nehmt wohl diese Gründe nicht ernsthaft, und doch gehen all derartige Betrachtungen auf die Pythagoreer zurück, die den Zahlen eine so hohe Bedeutung beilegten. Es scheint, als ob Ihr, der Ihr Mathematiker seid und, wie ich glaube, in vielen Fragen Anhänger der pythagoreischen Schule, auf einmal deren Mysterien geringschätzig behandelt.

Göttlichkeit des menschlichen Intellekts, weil er das Wesen der Zahlen begreift, nach Ansicht Platos.

Die pythagoreischen Zahlengeheimnisse sind Märchen.

Salv.Dass bei den Pythagoreern die Wissenschaft von den Zahlen im höchsten Ansehen stand, und sogar Plato 11den menschlichen Intellekt bloß darum bewunderte und ihn als gleichartig mit der göttlichen Vernunft betrachtete, weil er das Wesen der Zahlen begreife, ist mir wohlbekannt, ja ich neige der nämlichen Ansicht zu. Aber ich bin weit davon entfernt zu glauben, dass die geheimnisvollen Eigenschaften, derentwegen Pythagoras und seine Schule die Zahlenlehre so hoch schätzten, jene Albernheiten sein sollten, die im Volksmunde und in den landläufigen Büchern spuken. Ich weiß vielmehr, dass sie jene Wunder nicht den Schmähungen und der Verachtung des großen Haufens preisgeben wollten, dass sie die Veröffentlichung der tief verborgenen Zahleneigenschaften und der von ihnen entdeckten inkommensurabeln und irrationalen Größen als eine Profanation verurteilten und lehrten, dass, wer sie offenbare, dafür im Jenseits zu büßen habe. Einer oder der andere mag daher, um den gemeinen Mann abzuspeisen und sich seinen Fragen zu entziehen, ihm gesagt haben, die Zahlengeheimnisse bestünden in jenen Spielereien, die sich nachher im Volke verbreiteten. Es war das ebenso vorsichtig und bedacht, wie das Verfahren jenes klugen jungen Mannes, der seiner Mutter oder seiner neugierigen Frau – ich weiß nicht mehr sicher –, die ihn bestürmte, ihr die geheimen Verhandlungen des Senats mitzuteilen, ein Märchen aufband, um ihre lästigen Fragen los zu werden, so dass sie nebst vielen anderen Weibern vor selbigem Senate sich aufs Höchste lächerlich machten. 12

Simpl.Ich gehöre nicht zu denen, welche nach den Mysterien der Pythagoreer sonderlich lüstern sind. Aber ich entgegne, um auf unseren Gegenstand zurückzukommen: Die von Aristoteles vorgebrachten Gründe dafür, dass die Anzahl der Dimensionen mehr als drei weder beträgt, noch betragen kann, erscheinen mir zwingend; auch glaube ich, dass, wenn es einen strengeren Beweis gäbe, Aristoteles ihn nicht verschwiegen hätte.

Sagr.Setzt wenigstens hinzu, wenn er ihn gekannt oder sich seiner erinnert hätte. Aber Ihr, Signore Salviati, würdet mir einen großen Gefallen tun, wenn Ihr einen augenscheinlichen Beweis beibringen wolltet; nur muss er so fasslich sein, dass ich ihn verstehen kann.

Salv.Nicht nur Ihr, auch Signore Simplicio wird ihn verstehen, ja er ist Euch, wenn auch unbewussterweise längst bekannt. 13Zu besserem Verständnis wollen wir Papier und Feder benutzen, die ich für solche Gelegenheiten hier schon bereit sehe, und eine kleine Zeichnung entwerfen. Wir markieren zunächst zwei Punkte A und B ; verbinde ich dieselben einmal durch die krummen Linien A C B und A D B , dann durch die Gerade A B , so frage ich Euch, welche dieser Linien nach Eurer Meinung die Entfernung zwischen den Endpunkten A und B bestimmt und weshalb?

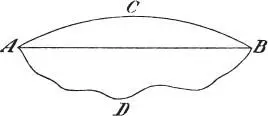
Sagr.Nach meiner Meinung die gerade Linie und nicht die krummen, teils weil jene die kürzeste ist, teils weil sie einzig in ihrer Art und bestimmt ist, während es von den anderen unzählige gibt, die untereinander ungleich und länger als die gerade Linie sind; jede Messung aber muss nach meiner Ansicht von dem ausgehen, was einzig in seiner Art und selber bestimmt ist.

Salv.Wir haben also in der geraden Linie ein Maß für die Strecke zwischen zwei Punkten. Fügen wir jetzt eine andere gerade Linie hinzu, welche der Linie A B parallel ist und C D heißen möge, so dass zwischen beiden eine Fläche gelegen ist; ich möchte, dass Ihr mir die Breite derselben angeben wolltet. Sagt mir also, nach welchem Punkte und in welcher Weise Ihr, von dem Endpunkte A ausgehend, zu der Linie C D gelangen wollt, um mir die Breite des zwischen beiden Linien enthaltenen Flächenstücks anzugeben; ich meine, ob Ihr dieselbe bestimmen wollt mittels der Länge der Kurve A E oder der Geraden A F oder ...