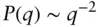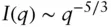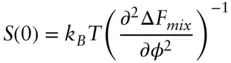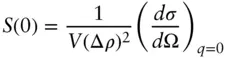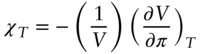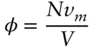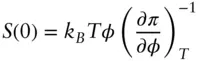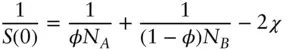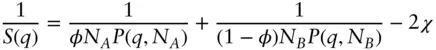The integral over Rij can be evaluated using
(1.104) 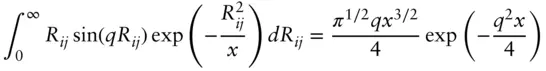
where x = (2| i − j | b 2)/3. Substituting in Eq. (1.102)we obtain
(1.105) 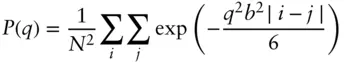
For a large chain ( N large), the summations can be replaced by integrals
(1.106) 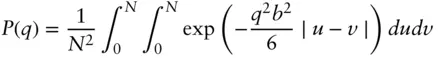
This can be evaluated [61] to give
( 1.107) 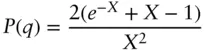
Here 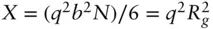 ( b denotes a statistical segment length). Eq. (1.107)is the Debye form factor function for a polymer. Figure 1.21shows an example of a computed Debye function. This function has a Guinier‐like asymptote at low q , but at high q ( qR g≫ 1),
( b denotes a statistical segment length). Eq. (1.107)is the Debye form factor function for a polymer. Figure 1.21shows an example of a computed Debye function. This function has a Guinier‐like asymptote at low q , but at high q ( qR g≫ 1), 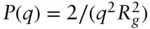 , i.e. it shows a scaling:
, i.e. it shows a scaling:
( 1.108) 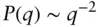
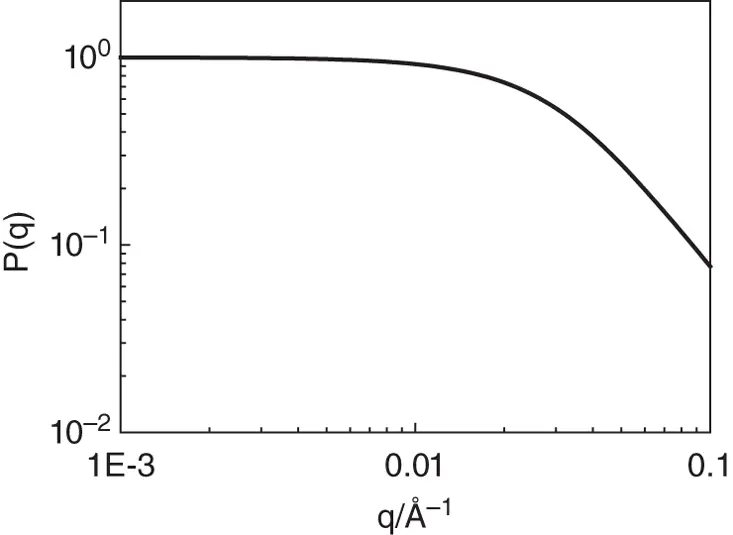
Figure 1.21 Debye form factor for a polymer with Rg = 50 Å.
The expressions in Eqs. (1.107)( 1.108) are valid for dilute polymer solutions under theta (ideal solution) conditions. However, this form factor and scaling behaviour is most commonly observed for polymers in the melt, which can adopt an ideal conformation since the local density within a polymer in the melt is the same as that at the macroscopic scale meaning that individual polymer chains are not perturbed by inter‐chain interactions [20, 62]
The Debye form factor can be generalized to the case of expanded/collapsed coils for which Rg = bN ν, where v is the Flory exponent ( v = 1/2 for Gaussian coils such as polymer chains in a theta solvent, v ≈ 3/5 for polymers in good solvents, v = 1/3 in a poor solvent). For a polymer with excluded volume, the intensity scales approximately as
(1.109) 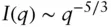
A closed‐form expression for the form factor is not available in this case, although approximate equations have been presented [63]. A more accurate exponent for polymers in good solvents is ν = 0.588 rather than ν = 0.6, this being obtained from sophisticated theoretical analysis (renormalization group theory) [61]. Figure 1.22compares the overall form factors of random coils (Gaussian chains) and those for excluded volume chains, indicating the Guinier regime, the power law scaling regimes and the high q regime where a scaling I ( q ) ∼ q −1from local stiffness is observed, this being the scaling behaviour for a rod ( Eq.(1.85) (1.77)).
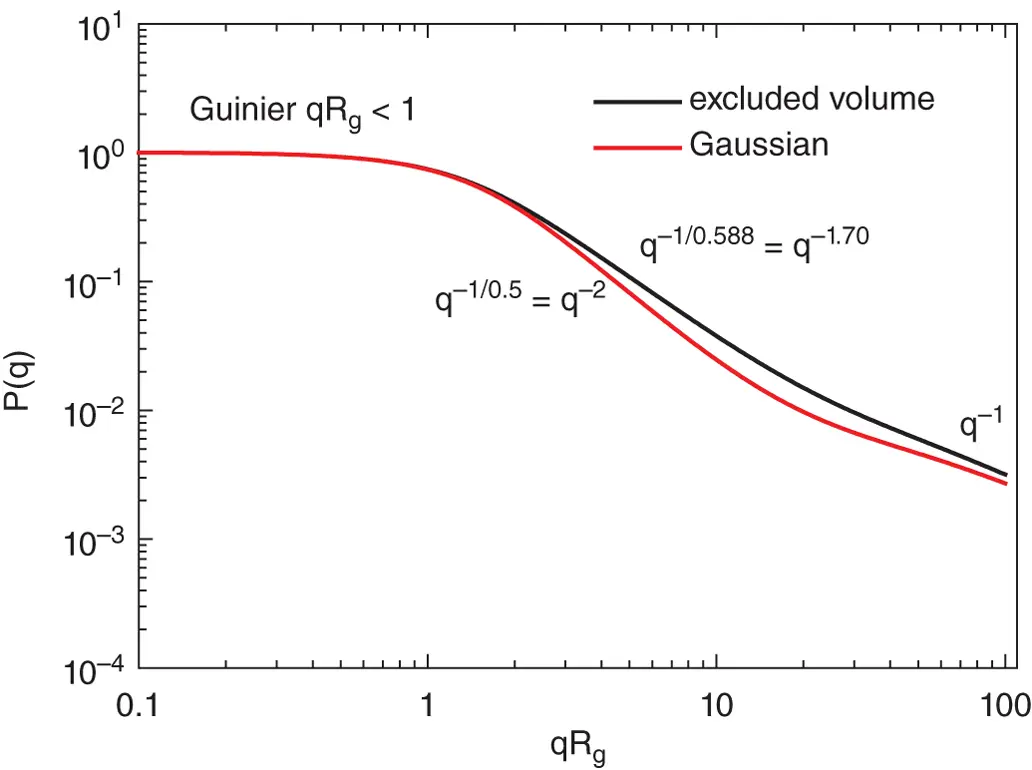
Figure 1.22 Comparison of form factor for random walk (Gaussian) chains and excluded volume chains with scaling laws indicated, also showing Guinier regime and effect of local stiffness ( q −1scaling of intensity) at very high q .
For polymers in solution with polymer volume fraction ϕ , or binary blends of polymers with volume fraction ϕ of chain A with degree of polymerization N A(and 1 − ϕ , N Bfor chain B and Flory‐Huggins interaction parameter of the pair, χ ), the structure factor at q = 0 can be obtained from the general compressibility relationship in terms of the free energy change on mixing Δ Fmix :
(1.110) 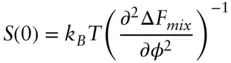
This is related to Eq. (2.8), first noting that the dimensionless structure factor (note q , V , and Δρ should be in consistent units) at q = 0 is given by
(1.111) 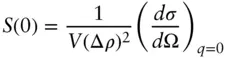
where V is the volume of the system and using the relationship between isothermal compressibility χT and osmotic pressure, π [12]:
( 1.112) 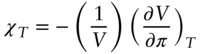
The volume fraction can be written [12, 49]
(1.113) 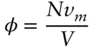
where N / V is the number density and vm molar volume (of solute in the case of a polymer solution). Use of Eq. (2.8)(with Δρ for the contrast in a solution) leads to [49]
( 1.114) 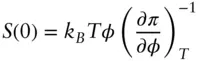
Using the relationships between osmotic pressure and chemical potential and recalling that chemical potential can be written as a free energy gradient, Eq. (1.114)may be obtained from Eq. (1.112). The details of the derivation are available elsewhere [12, 49].
Using the free energy change of mixing Δ F mixfrom Flory‐Huggins theory gives
(1.115) 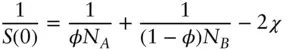
This is generalized for non‐zero wavenumbers using the random‐phase approximation (RPA) to give [12, 49, 61, 64]
( 1.116) 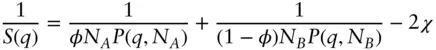
Here P ( q , N ) is the corresponding form factor of an ideal chain, i.e. the Debye function ( Eq. (1.107)). These expressions apply to the case of polymers in solution, the subscripts A and B referring to solvent and solute. These expressions are also useful for the case of blends of protonated and deuterated polymers in SANS studies (see Section 5.8), where A and B label the respective unlabelled and labelled chains. The RPA is a mean field method, widely employed in polymer science to calculate the structure factor in terms of the form factor of single chains [62].
Читать дальше

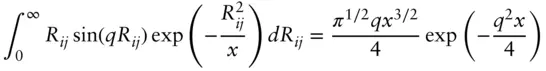
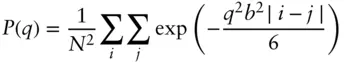
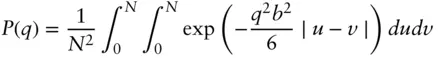
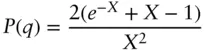
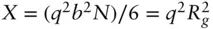 ( b denotes a statistical segment length). Eq. (1.107)is the Debye form factor function for a polymer. Figure 1.21shows an example of a computed Debye function. This function has a Guinier‐like asymptote at low q , but at high q ( qR g≫ 1),
( b denotes a statistical segment length). Eq. (1.107)is the Debye form factor function for a polymer. Figure 1.21shows an example of a computed Debye function. This function has a Guinier‐like asymptote at low q , but at high q ( qR g≫ 1), 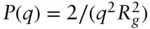 , i.e. it shows a scaling:
, i.e. it shows a scaling: