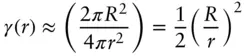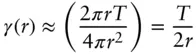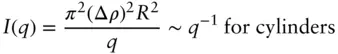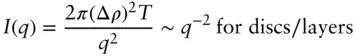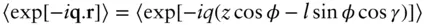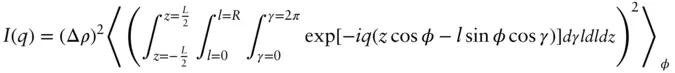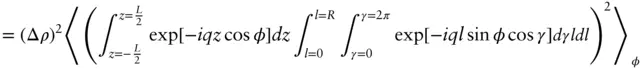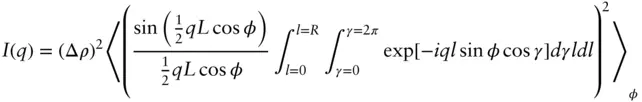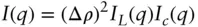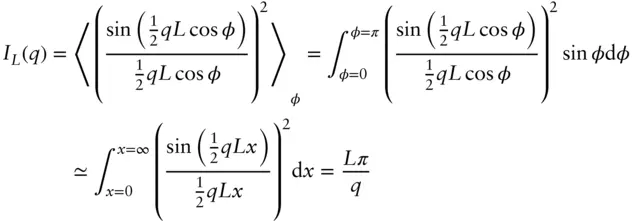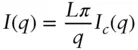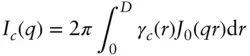Ian W. Hamley - Small-Angle Scattering

The form factors for particulate systems of different dimensionality can all be expressed in terms of hypergeometric functions [27].

The scaling behaviour of the intensity (plotted on a double logarithmic scale) at low q for monodisperse and uniform spheres, long cylinders and flat particles (disc or layer structures) is shown in Figure 1.17, along with examples of calculated form factors (examples of experimental data corresponding to this type of structure are presented in Section 4.13). For spherical particles, the slope is almost zero (it cannot be exactly zero according to the Guinier equation, Eq. (1.24)). For a long cylinder I ∼ q −1at low q whereas for a flat particle such as a disc or a bilayer structure I ∼ q −2at low q .

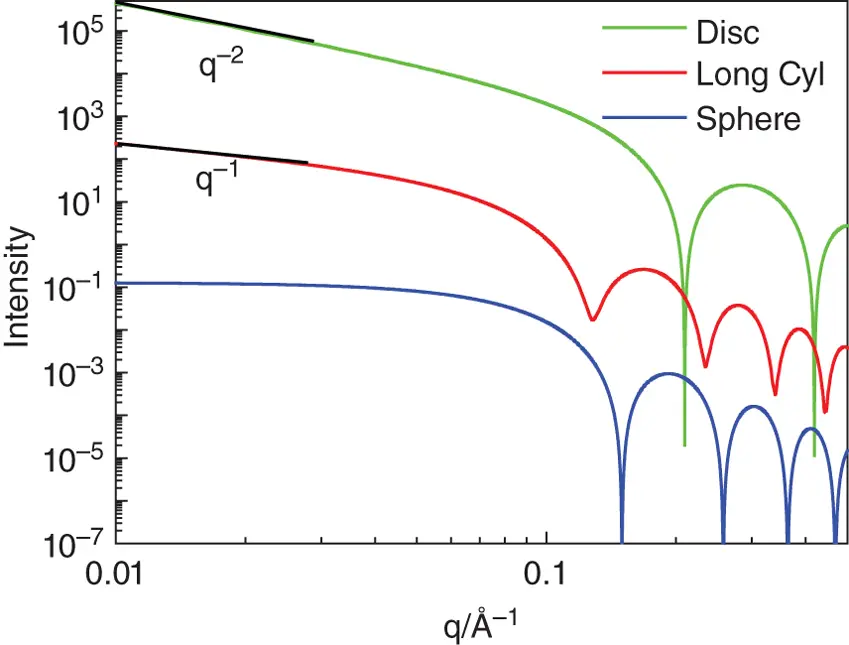
Figure 1.17 Form factors calculated for homogeneous particles along with limiting slopes. Form factors are calculated for spheres of radius R = 30 Å, cylinders of radius R = 30 Å and length L = 1000 Å and discs with thickness T = 30 Å and radius R = 1000 Å. The calculated profiles have been offset vertically for convenience. The minima in principle have zero intensity, but are truncated due to numerical calculation accuracy and for convenience plotting on a logarithmic intensity scale. The profiles were calculated using SASfit [21].

These scaling behaviours for extended rod‐like and flat particles can be derived as discussed in the following section.

Alternatively, the scaling behaviour can be obtained from the behaviours of the autocorrelation functions at large r (relating to low q behaviour of the intensity). For cylinders (radius R ), [56]

( 1.83)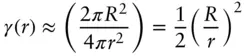

For flat particles (thickness T ) [56]

( 1.84)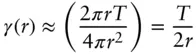

Substitution of these expressions into Eq. (1.8)leads to the following equations: [56]

(1.85)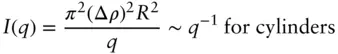

(1.86)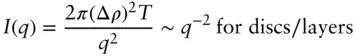

For monodisperse spherical particles of radius R , the minima in the form factor are located at qR = 4.493, 7.725... [10]. For an isotropic system of long cylindrical rods (radius R ), the form factor minima are located at qR = 3.83, 7.01… [10] and for flat particles (thickness T ) at qT /2 = 3.14, 6.28… These values can be obtained from the minima in the corresponding Bessel or sine functions as in the equations in Section 1.7.3.

It should be noted that the form factors and the position of the minima in them depend on products of q and an appropriate particle dimension; therefore, the form factors have the same appearance for different pairs of reciprocal units (i.e. calculations with q in Å −1with dimensions in Å or q in nm −1with dimensions in nm give the same result).

For a long cylindrical particle the scattering intensity (form factor) can be computed from Eq. (1.6)by calculating the average exp[− i q. r] in polar coordinates ( l , z , γ ), where the qvector and vector rto a point in the cylinder are related by the polar angles ( ϕ , γ ) ( Figure 1.18):

(1.87)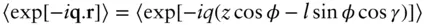

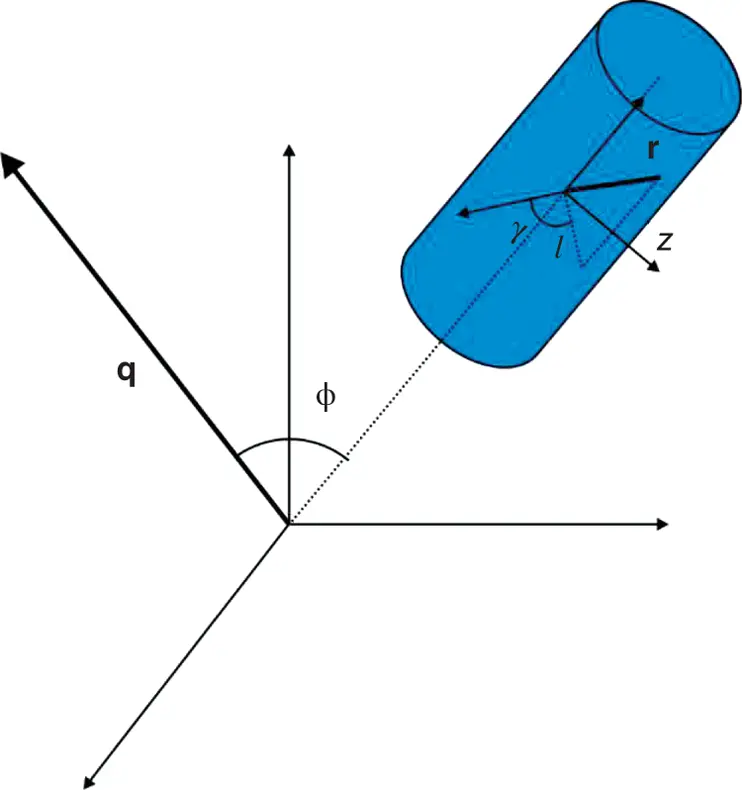
Figure 1.18 Inter‐relationship between vectors qand rin cylindrical co‐ordinates.

For a uniform cylinder (radius R , length L ) this leads to the expression [57]

(1.88)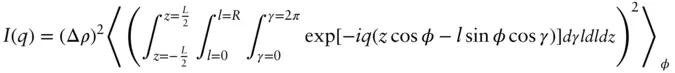

(1.89)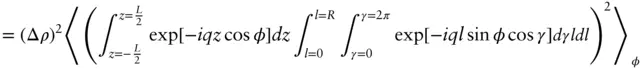

Performing the integral over z (using the same formula as in Eq. (1.12)) we have

(1.90)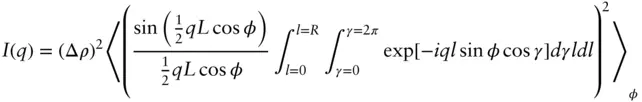

For L > > R we can factor this as the product of intensity associated with the length of the particle IL ( q ) and that of the cross‐section Ic ( q ) (i.e. the intensity is written as a convolution product):

(1.91)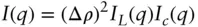

where

(1.92)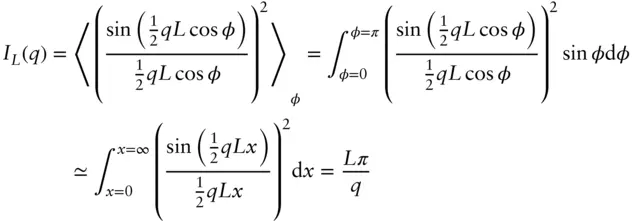

The integral over ϕ extends to infinity to make use of the Dirichlet integral, this is valid when q ≥ 2 π / L , since the integrand is negligibly small for x > 1 [7]. This leads to the factorization [5, 6]

( 1.93)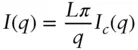

where Ic ( q ) is the form factor of the cross‐section. As mentioned above, this is valid when L > > R . Eq. (1.93)shows the I ( q ) ∼ q −1scaling for a cylindrical particle at low q (where IL ( q ) dominates). This derivation is for a uniform cylinder for which Ic ( q ) can be evaluated as in the following, however Eq. (1.93)applies in general for other rod‐like particles.

The cross‐section intensity is related to the distance distribution function of the cross‐section, γc ( r ), via the expression [6, 7]

(1.94)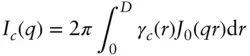

Here D is the cross‐section diameter. For a uniform cylinder this may be evaluated to give [6]