1 Cover
2 Title Page Waves and Scattering Set coordinated by Jean-Michel L. Bernard Volume 1
3 Copyright Page First published 2020 in Great Britain and the United States by ISTE Ltd and John Wiley & Sons, Inc. Apart from any fair dealing for the purposes of research or private study, or criticism or review, as permitted under the Copyright, Designs and Patents Act 1988, this publication may only be reproduced, stored or transmitted, in any form or by any means, with the prior permission in writing of the publishers, or in the case of reprographic reproduction in accordance with the terms and licenses issued by the CLA. Enquiries concerning reproduction outside these terms should be sent to the publishers at the undermentioned address: ISTE Ltd 27-37 St George’s Road London SW19 4EU UK www.iste.co.uk John Wiley & Sons, Inc. 111 River Street Hoboken, NJ 07030 USA www.wiley.com © ISTE Ltd 2020 The rights of Vito G. Daniele and Guido Lombardi to be identified as the authors of this work have been asserted by them in accordance with the Copyright, Designs and Patents Act 1988. Library of Congress Control Number: 2020938054 British Library Cataloguing-in-Publication Data A CIP record for this book is available from the British Library ISBN 978-1-78630-263-2
4 Preface
5 Introduction
6 1 Introduction to the Wiener-Hopf Method1.1 A brief history of the Wiener-Hopf method 1.2 Fundamental definitions and assumptions to develop the Wiener-Hopf technique in the spectral domain 1.3 WH equations from the physical domain to the spectral domain 1.4 WH equations in wave scattering problems 1.5 Classical solution of WH equations 1.6 The decomposition (Cauchy) equations 1.7 General formula for factorization of scalar kernels 1.8 Some explicit factorization of matrix kernels useful in wedge scattering 1.9 The Fredholm factorization technique: a general technique to solve WH equations 1.10 Spectral properties of the unknowns 1.11 Semi-analytical solution of the Fredholm integral equation 1.12 Analytic continuation outside the integration line in the η -plane 1.13 The complex plane w 1.14 The WH unknowns in the w plane 1.15 The Fredholm factorization technique in the w plane 1.16 Analytic continuation in the w plane 1.17 The Fredholm factorization technique to factorize the kernel 1.18 Some examples of the Fredholm factorization method Appendix 1.A: effect of using j and i as imaginary units in Fourier transforms Appendix 1.B: compactness of the matrix kernel 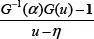
7 2 A Basic Example: Scattering by a Half-plane2.1. The fundamental problem of diffraction in wave motion 2.2. Unified theory of transverse equations in arbitrary stratified regions 2.3. WH equation for electromagnetic diffraction by a perfectly electrically conducting (PEC) half-plane illuminated by an Ez-polarized plane wave at normal incidence 2.4. Non-standard contributions of WH unknowns in the PEC half-plane illuminated by an Ez-polarized plane wave at normal incidence 2.5. Solution of the WH equation of the PEC half-plane using classical closed-form factorization 2.6. Solution of the WH equation of the PEC half-plane using the Fredholm factorization method 2.7. Field estimation 2.8. Numerical validation of the Fredholm factorization method 2.9. Generality of the wave motion in a homogeneous isotropic elastic solid 2.10. Plane waves in a homogeneous elastic solid and simplifications 2.11. Diffraction by a half-infinite crack in a homogeneous elastic solid planar problem 2.12. Diffraction by a half-infinite crack in a homogeneous isotropic two-dimensional elastic solid problem
8 3 The Wiener-Hopf Theory for Angular Region Problems3.1. A brief history of the classical methods for studying angular regions 3.2. Introduction to the generalized Wiener-Hopf technique 3.3. WH functional equations in the angular region filled by a homogeneous isotropic medium in Electromagnetics 3.4. Reduction of the generalized functional equations of an angular region to functional equations defined in the same complex plane 3.5. Generalized Wiener-Hopf equations for the impenetrable wedge scattering problem 3.6. Solution of generalized Wiener-Hopf equations for the impenetrable wedge scattering problem 3.7. Non-standard parts of the plus and minus functions in GWHEs for the impenetrable wedge scattering problem 3.8. Closed-form solution of the PEC wedge scattering problem at normal incidence 3.9. Alternative solution of the PEC wedge scattering problem at normal incidence via difference equations 3.10. Generalized WH functional equations for angular regions in the w plane 3.11. Rotating wave method 3.12. Properties of rotating waves 3.13. Spectral field component in w for an arbitrary direction ϕ using rotating waves 3.14. Rotating waves in areas different from electromagnetism 3.15. Closed-form solution of the diffraction of an elastic SH wave by wedge with classical factorization 3.16. Rotating waves with the MF transform for wedge problems 3.17. Alternative solution of PEC wedge scattering problems via difference equations and the MF transform in terms of rotating waves Appendix 3.A: the Malyuzhinets–Fourier (MF) transform
9 References
10 Index
11 Summary of Volume 2
12 Other titles from ISTE in Waves
13 End User License Agreement
1 Chapter 1Figure 1.6.1 The “smile” and “frown” integration lines of the η' -plane Figure 1.13.1 Proper sheet of the η-plane with four quadrants 1, 2, 3 and 4 deli...Figure 1.13.2 Image of the proper and improper sheets of the η-plane onto the w ...Figure 1.15.1 Contour deformation of the integration line from the real axis of ...Figure 1.15.2 Integration path λ in the w plane. For a color version of the figu...Figure 1.18.1 Top left: the absolute value of F+(η) obtained with the Mittag–Lef...Figure 1.18.2 Top: the absolute value of the component (i,j) of the plus factori...Figure 1.18.3 Left: the absolute value of the component s (s=1 gray symbols, s=2...
2 Chapter 2Figure 2.2.1 Left: slab filled by an arbitrary linear medium. Right: network...Figure 2.3.1 The perfectly electrically conducting (PEC) half-plane problem ...Figure 2.7.1 Equivalence theorem using a perfectly electrically conducting s...Figure 2.7.2 Plane η: branch points ±k, vertical branch lines, curves with...Figure 2.7.3 Left: η-plane with the SDP for the set of φ = {πFigure 2.8.1 The half-plane scattering problem with Eo=1 V/m, φFigure 2.8.2 The half-plane scattering problem with Eo=1 V/m, φ oFigure 2.8.3 Half-plane scattering problem with Eo=1 V/m, φ o= 0...Figure 2.8.4 Half-plane scattering problem with Eo=1 V/m, φ o= 0...Figure 2.9.1 Left: slab filled by an arbitrary linear medium in elasticity. ...Figure 2.9.2 Left: multilayer slab in elasticity terminated by semi-infinite...Figure 2.10.1 Left: plane wave reflection between semi-infinite homogeneous ...Figure 2.11.1 Left: half-infinite crack in a homogeneous elastic solid plana...
3 Chapter 3Figure 3.3.1 Angular region 0 ≤ Φ ≤ γ 1≤ Π with three coordina...Figure 3.3.2 Space divided into four angular regions delimited by ϕ =...Figure 3.4.1 Proper sheet of the 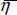 -plane with four quadrants 1, 2, 3 and 4 d...Figure 3.4.2 Images of the proper and improper sheets of the
-plane with four quadrants 1, 2, 3 and 4 d...Figure 3.4.2 Images of the proper and improper sheets of the 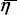 -plane in the...Figure 3.5.1 Scattering of an impenetrable wedge by a plane wave at skew inc...Figure 3.11.1 Angular region 0 ≤ ρ < ∞, ϕ 1≤ ϕ ≤ ϕ...Figure 3.12.1 Regularity regions of
-plane in the...Figure 3.5.1 Scattering of an impenetrable wedge by a plane wave at skew inc...Figure 3.11.1 Angular region 0 ≤ ρ < ∞, ϕ 1≤ ϕ ≤ ϕ...Figure 3.12.1 Regularity regions of 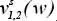 respectively in
respectively in 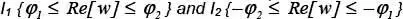 .Figure 3.12.2 Images of the proper and improper sheets of the η-plane in the...Figure 3.13.1 Angular region 0 ≤ ρ < ∞, ϕ 1≤ ϕ ≤ ϕ...Figure 3.15.1 Elastic solid wedge illuminated by an SH wave. For a color ver...Figure 3.17.1 Left: PEC wedge illuminated by a plane wave at Ez polarization...Figure 3.A.1 Graphical representation of natural and complex spectral planes...
.Figure 3.12.2 Images of the proper and improper sheets of the η-plane in the...Figure 3.13.1 Angular region 0 ≤ ρ < ∞, ϕ 1≤ ϕ ≤ ϕ...Figure 3.15.1 Elastic solid wedge illuminated by an SH wave. For a color ver...Figure 3.17.1 Left: PEC wedge illuminated by a plane wave at Ez polarization...Figure 3.A.1 Graphical representation of natural and complex spectral planes...
Читать дальше

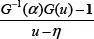
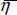 -plane with four quadrants 1, 2, 3 and 4 d...Figure 3.4.2 Images of the proper and improper sheets of the
-plane with four quadrants 1, 2, 3 and 4 d...Figure 3.4.2 Images of the proper and improper sheets of the 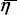 -plane in the...Figure 3.5.1 Scattering of an impenetrable wedge by a plane wave at skew inc...Figure 3.11.1 Angular region 0 ≤ ρ < ∞, ϕ 1≤ ϕ ≤ ϕ...Figure 3.12.1 Regularity regions of
-plane in the...Figure 3.5.1 Scattering of an impenetrable wedge by a plane wave at skew inc...Figure 3.11.1 Angular region 0 ≤ ρ < ∞, ϕ 1≤ ϕ ≤ ϕ...Figure 3.12.1 Regularity regions of 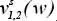 respectively in
respectively in 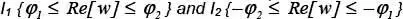 .Figure 3.12.2 Images of the proper and improper sheets of the η-plane in the...Figure 3.13.1 Angular region 0 ≤ ρ < ∞, ϕ 1≤ ϕ ≤ ϕ...Figure 3.15.1 Elastic solid wedge illuminated by an SH wave. For a color ver...Figure 3.17.1 Left: PEC wedge illuminated by a plane wave at Ez polarization...Figure 3.A.1 Graphical representation of natural and complex spectral planes...
.Figure 3.12.2 Images of the proper and improper sheets of the η-plane in the...Figure 3.13.1 Angular region 0 ≤ ρ < ∞, ϕ 1≤ ϕ ≤ ϕ...Figure 3.15.1 Elastic solid wedge illuminated by an SH wave. For a color ver...Figure 3.17.1 Left: PEC wedge illuminated by a plane wave at Ez polarization...Figure 3.A.1 Graphical representation of natural and complex spectral planes...










