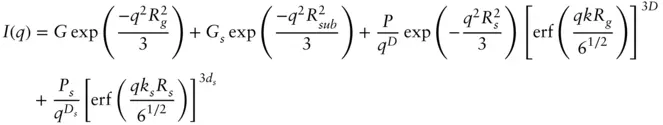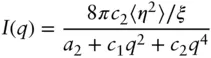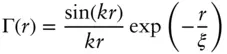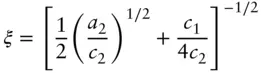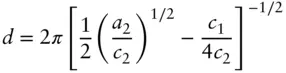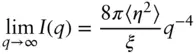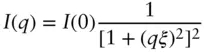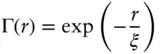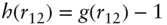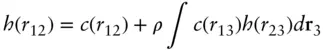Ian W. Hamley - Small-Angle Scattering

A generalized Beaucage function is used for a system with two structural levels with radius of gyration Rg for the fractal and Rsub for the subunits [41]

( 1.65)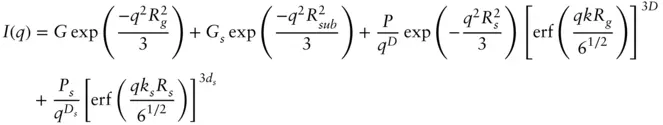

Here k is an empirical constant, k ≈ 1 [41], and Gs , Ps are the Guinier and Porod scaling terms for the subunit components of the intensity, ds is the fractal dimension for the subunits with size Rs , and P and D are as defined in Eqs. (1.63)and (1.64). This function has a large number of parameters and can be used to fit SAS data from many multilevel systems. Figure 1.13shows an example of a calculated generalized Beaucage form factor along with the components corresponding to the corresponding terms in Eq. (1.65).

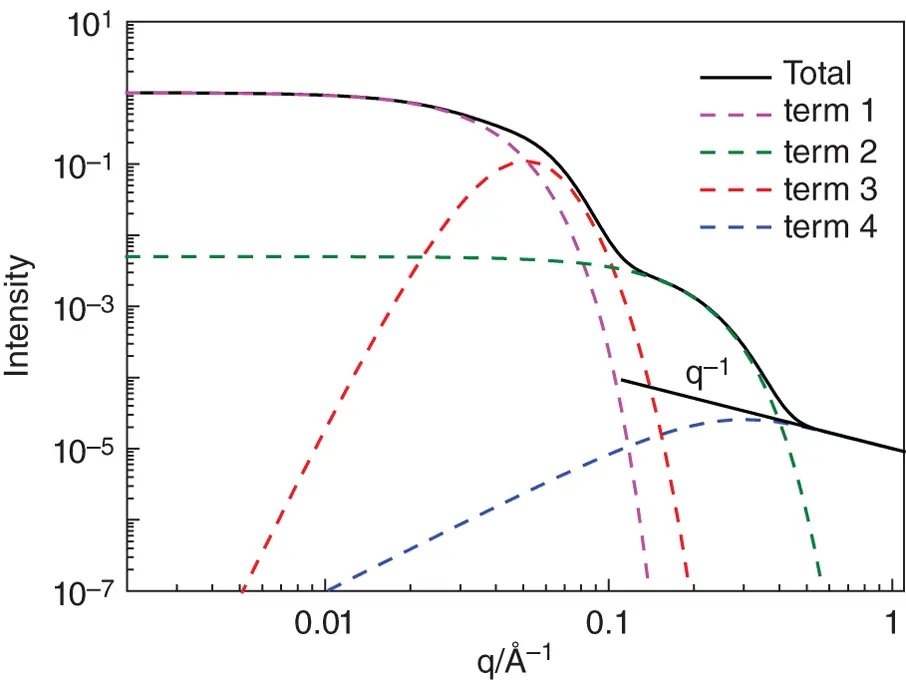
Figure 1.13 Example of calculated form factor using the generalized Beaucage form factor, Eq. (1.65)along with the components of this equation. Calculation for G = 1, P = 1 × 10 −4, Gs = 5 × 10 −3, Ps = 1 × 10 −5, Rg = 50 Å, Rsub = 30 Å, Rs = 10 Å, k = 1, ks = 1, D = 4, D s= 1 (limiting Porod slope shown). Calculated using SASfit (Table 2.2).

The low q scaling from a fractal structure shows a power law behaviour, I ( q ) ∼ q −Din a range 1/ Rg ≪ q ≪ 1/ Rs [12]. Further details on SAS studies of fractal systems are available in a dedicated text [42].

A widely used expression for the scattering from bicontinuous microemulsions is due to Teubner and Strey. The intensity is computed from a phenomenological Landau–Ginzburg free energy expansion including gradient terms of the composition order parameter. The structure factor (as in the previous section written as an intensity) is given by [43, 44]:

( 1.66)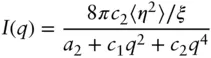

The terms a 2, c 1, c 2are coefficients in the free energy expansion and for a microemulsion, c 1< 0 while a 2> 0 and c 2> 0. The term 〈 η 2〉 = ϕ 1 ϕ 2(Δ ρ ) 2represents a weighted difference in scattering densities between the two phases with volume fractions ϕ 1and ϕ 2. The corresponding real‐space correlation function related to Eq. (1.66)by a Fourier transform is

( 1.67)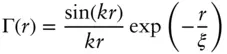

Here k = 2π/ d . There are two length scales associated with the microemulsion, the correlation length given by

(1.68)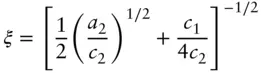

and the domain size given by

(1.69)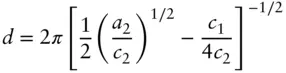

Figure 1.14shows an example of fitting SAXS data for a microemulsion using the Teubner‐Strey structure factor. The intensity at high q in the Teubner‐Strey equation shows limiting Porod behaviour:

(1.70)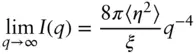

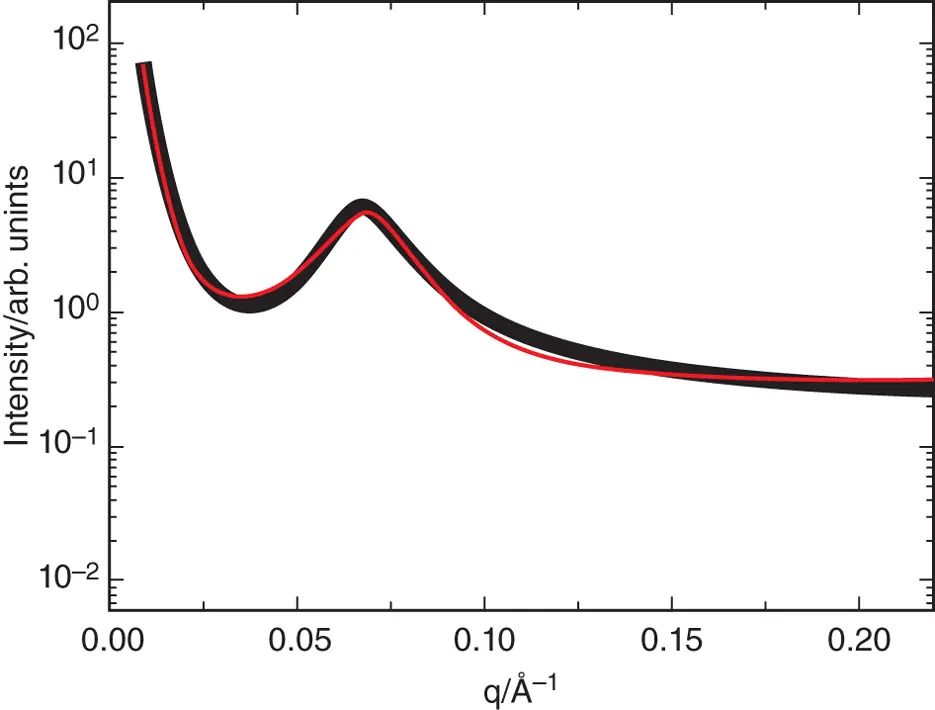
Figure 1.14 Example of SAXS data for a bicontinuous microemulsion (Pluronic copolymer with tannic acid in aqueous solution) (open symbols), fitted to the Teubner‐Strey structure factor (red line).

Source : From Dehsorkhi et al. [45]. © 2011, Royal Society of Chemistry.

Berk gave an alternative (more complex) expression for Γ( r ) for a random wave model, which can also be used to describe bicontinuous microemulsions [46].

For a two‐phase system with a preferred correlation length, the Debye‐Bueche structure factor, sometimes known as the Debye‐Anderson‐Brumberger model [47–49] may be used:

(1.71)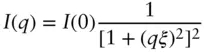

In this model, the correlation function exhibits a simple exponential decay:

( 1.72)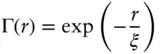

Here again, ξ is a correlation length. Comparison of Eqs. (1.72)and ( 1.67) shows that the Teubner‐Strey equation introduces the damped periodic function j 0( kr ) = sin( kr )/ kr into the correlation function. Figure 1.15shows examples of calculated intensity profiles with the Debye‐Bueche structure factor. The Debye‐Bueche model is obtained as a special case of the Teubner‐Strey model for very large d ‐spacing ( d ≫ ξ ). The intensity decays as q −4in the Porod regime at high q [48].

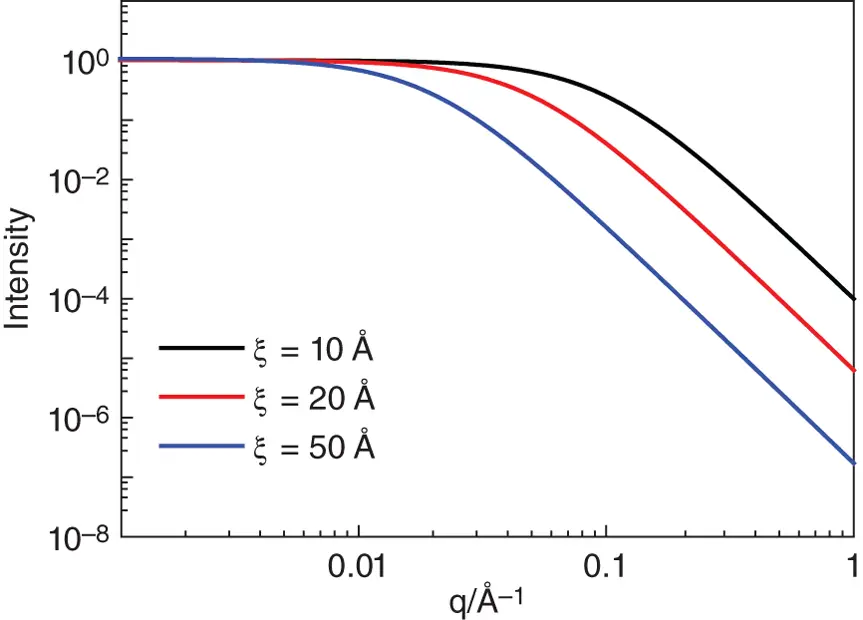
Figure 1.15 Calculated structure factors using the Debye‐Bueche structure factor with I (0) = 0 and the correlation lengths indicated.

Other types of microemulsion contain droplets, and the scattering can be described using models for the form and structure factors of globular objects.

The Ornstein‐Zernike (OZ) equation is an integral equation used in liquid state theory to describe the correlation between two molecules. Specifically, the total correlation function between particles at r 1and r 2, with inter‐particle separation r 12is written as

(1.73)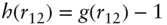

where g ( r ) is the radial distribution function. The OZ equation is [50]

( 1.74)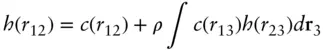

Here c ( r ) are direct correlation functions and ρ is the density. This integral equation gives the total correlation function as the sum of the direct correlation and an integral over the indirect correlations involving a third particle, integrating over its position r 3.