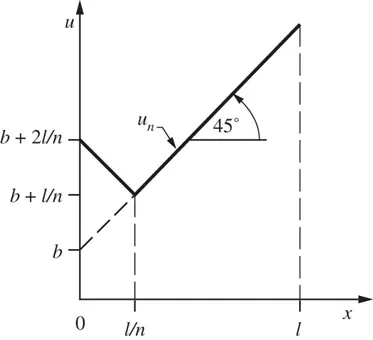
Figure 1.2 Exercise 1.3: The function 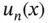 .
.
Remark 1.1  defined on
defined on  by eq. (1.20)satisfies the properties of linear forms listed in Section A.1.2if the following inequality is satisfied:
by eq. (1.20)satisfies the properties of linear forms listed in Section A.1.2if the following inequality is satisfied:
(1.35) 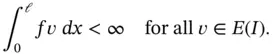
1.2.2 The principle of minimum potential energy
Theorem 1.2The function 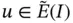 that satisfies
that satisfies 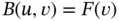 for all
for all 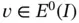 minimizes the quadratic functional 8
minimizes the quadratic functional 8 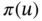 , called the potential energy;
, called the potential energy;
(1.36) 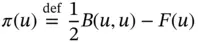
on the space 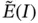 .
.
Proof: For any 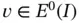 ,
, 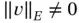 we have:
we have:
(1.37) 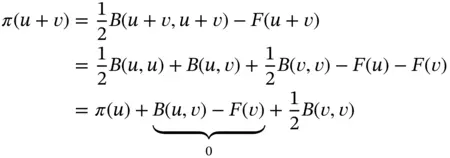
where 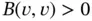 unless
unless 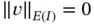 . Therefore any admissible nonzero perturbation of u will increase
. Therefore any admissible nonzero perturbation of u will increase 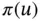 .
.
This important theorem, called the theorem or principle of minimum potential energy, will be used in Chapter 7as our starting point in the formulation of mathematical models for beams, plates and shells.
Given the potential energy and the space of admissible functions, it is possible to determine the strong form. This is illustrated by the following example.
Example 1.2Let us determine the strong form corresponding to the potential energy defined by
(1.38) 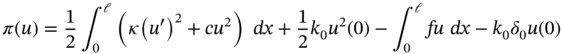
with 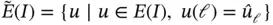 .
.
Since u minimizes 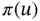 , any perturbation of u by
, any perturbation of u by 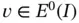 will increase
will increase 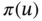 . Therefore
. Therefore 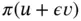 is minimum at
is minimum at 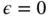 and hence
and hence
(1.39) 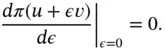
Therefore we have
(1.40) 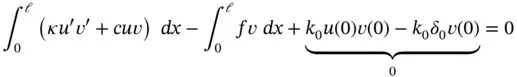
where the last two terms are zero because 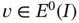 . Integrating the first term by parts,
. Integrating the first term by parts,
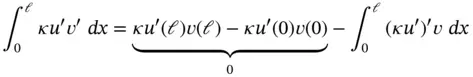
and, substituting this into eq. (1.40), we get
(1.41) 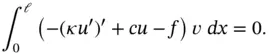
Since this holds for all 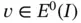 , the bracketed expression must be zero. In other words, the solution of the differential equation
, the bracketed expression must be zero. In other words, the solution of the differential equation
(1.42) 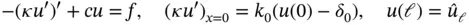
minimizes the potential energy defined by eq. (1.38). This is the strong form of the problem.
Remark 1.2The procedure in Example 1.2is used in the calculus of variations for identifying the differential equation, known as the Euler 9 ‐Lagrange 10 equation, the solution of which maximizes or minimizes a functional. In this example the solution minimizes the potential energy on the space 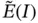 .
.
Remark 1.3Whereas the strain energy is always positive, the potential energy may be positive, negative or zero.
1.3 Approximate solutions
The trial and test spaces defined in the preceding section are infinite‐dimensional, that is, they span infinitely many linearly independent functions. To find an approximate solution, we construct finite‐dimensional subspaces denoted, respectively, by  ,
, 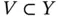 and seek the function
and seek the function 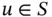 that satisfies
that satisfies 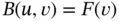 for all
for all 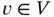 . Let us return to the introductory example described in Section 1.1and define
. Let us return to the introductory example described in Section 1.1and define
Читать дальше


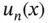 .
.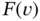 defined on
defined on 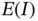 by eq. (1.20)satisfies the properties of linear forms listed in Section A.1.2if the following inequality is satisfied:
by eq. (1.20)satisfies the properties of linear forms listed in Section A.1.2if the following inequality is satisfied: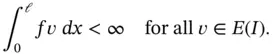
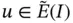 that satisfies
that satisfies 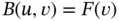 for all
for all 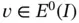 minimizes the quadratic functional 8
minimizes the quadratic functional 8 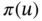 , called the potential energy;
, called the potential energy;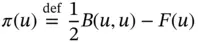
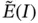 .
.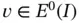 ,
, 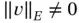 we have:
we have: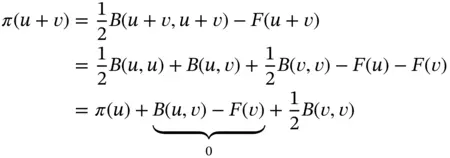
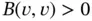 unless
unless 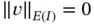 . Therefore any admissible nonzero perturbation of u will increase
. Therefore any admissible nonzero perturbation of u will increase  .
.
 .
. , any perturbation of u by
, any perturbation of u by  will increase
will increase 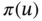 . Therefore
. Therefore 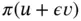 is minimum at
is minimum at 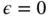 and hence
and hence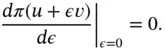
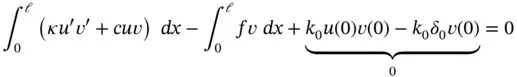
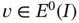 . Integrating the first term by parts,
. Integrating the first term by parts,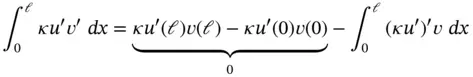
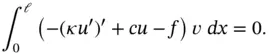
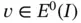 , the bracketed expression must be zero. In other words, the solution of the differential equation
, the bracketed expression must be zero. In other words, the solution of the differential equation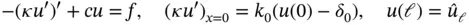
 .
. ,
,  and seek the function
and seek the function 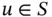 that satisfies
that satisfies 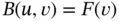 for all
for all 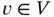 . Let us return to the introductory example described in Section 1.1and define
. Let us return to the introductory example described in Section 1.1and define










