1 ...6 7 8 10 11 12 ...36 (1.10) 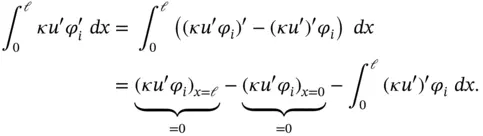
The underbraced terms vanish on account of the boundary conditions, see eq. (1.7). On substituting this expression into eq. (1.9), we get
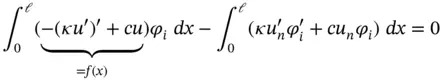
which will be written as
(1.11) 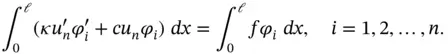
We define
(1.12) 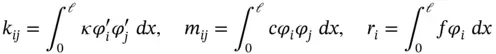
and write eq. (1.11)in the following form
(1.13) 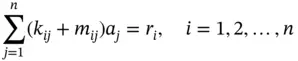
which represents n simultaneous equations in n unknowns. It is usually written in matrix form:
(1.14) 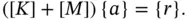
On solving these equations we find an approximation un to the exact solution u in the sense that un minimizes the integral 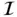 .
.
Example 1.1 Let  ,
, 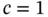 ,
, 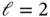 and
and
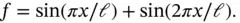
With these data the exact solution of eq. (1.5)is
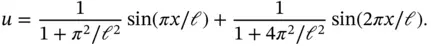
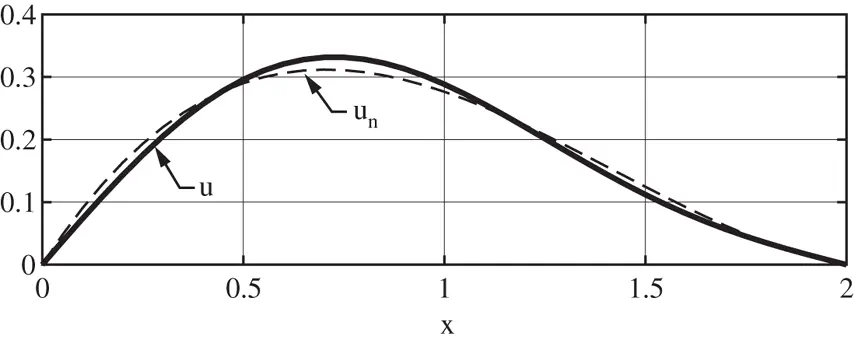
Figure 1.1 Exact and approximate solutions for the problem in Example 1.1.
We seek an approximation to u in the form:
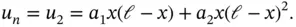
On computing the elements of 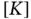 ,
, 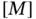 and
and 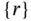 we get
we get
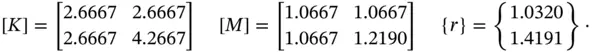
The solution of this problem is 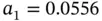 ,
, 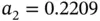 . These coefficients, together with the basis functions, define the approximate solution un . The exact and approximate solutions are shown in Fig. 1.1.
. These coefficients, together with the basis functions, define the approximate solution un . The exact and approximate solutions are shown in Fig. 1.1.
The choice of basis functions
By definition, a set of functions 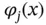 ,
, 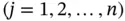 are linearly independent if
are linearly independent if
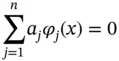
implies that 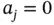 for
for 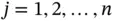 . It is left to the reader to show that if the basis functions are linearly independent then matrix
. It is left to the reader to show that if the basis functions are linearly independent then matrix 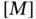 is invertible.
is invertible.
Given a set of linearly independent functions 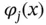 ,
, 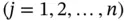 , the set of functions that can be written as
, the set of functions that can be written as
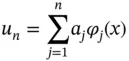
is called the span and 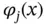 are basis functions of S .
are basis functions of S .
We could have defined other polynomial basis functions, for example;
(1.15) 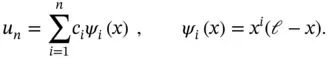
When one set of basis functions 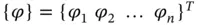 can be written in terms of another set
can be written in terms of another set 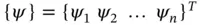 in the form:
in the form:
(1.16) 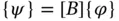
where 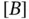 is an invertible matrix of constant coefficients then both sets of basis functions are said to have the same span. The following exercise demonstrates that the approximate solution depends on the span, not on the choice of basis functions.
is an invertible matrix of constant coefficients then both sets of basis functions are said to have the same span. The following exercise demonstrates that the approximate solution depends on the span, not on the choice of basis functions.
Exercise 1.1Solve the problem of Example 1.1using the basis functions 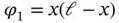 ,
, 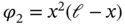 and show that the resulting approximate solution is identical to the approximate solution obtained in Example 1.1. The span of the basis functions in this exercise and in Example 1.1is the same: It is the set of polynomials of degree less than or equal to 3 that vanish in the points
and show that the resulting approximate solution is identical to the approximate solution obtained in Example 1.1. The span of the basis functions in this exercise and in Example 1.1is the same: It is the set of polynomials of degree less than or equal to 3 that vanish in the points 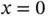 and
and 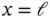 .
.
Читать дальше

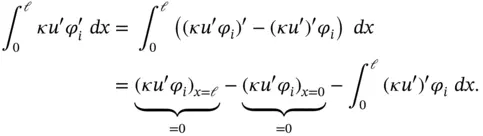
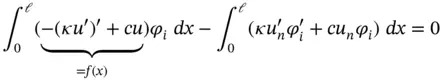
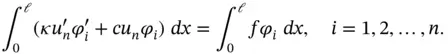
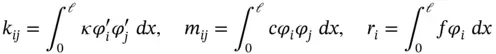
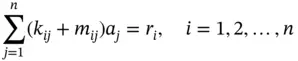
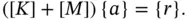
 .
.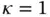 ,
,  ,
, 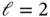 and
and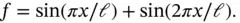
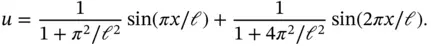

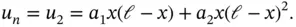
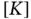 ,
, 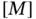 and
and 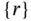 we get
we get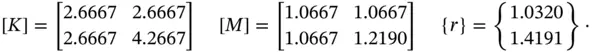
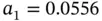 ,
, 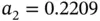 . These coefficients, together with the basis functions, define the approximate solution un . The exact and approximate solutions are shown in Fig. 1.1.
. These coefficients, together with the basis functions, define the approximate solution un . The exact and approximate solutions are shown in Fig. 1.1.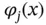 ,
, 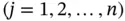 are linearly independent if
are linearly independent if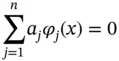
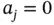 for
for 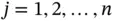 . It is left to the reader to show that if the basis functions are linearly independent then matrix
. It is left to the reader to show that if the basis functions are linearly independent then matrix 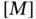 is invertible.
is invertible.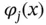 ,
, 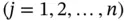 , the set of functions that can be written as
, the set of functions that can be written as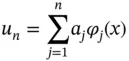
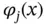 are basis functions of S .
are basis functions of S .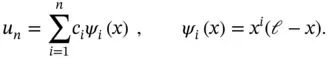
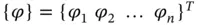 can be written in terms of another set
can be written in terms of another set 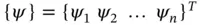 in the form:
in the form: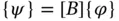
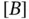 is an invertible matrix of constant coefficients then both sets of basis functions are said to have the same span. The following exercise demonstrates that the approximate solution depends on the span, not on the choice of basis functions.
is an invertible matrix of constant coefficients then both sets of basis functions are said to have the same span. The following exercise demonstrates that the approximate solution depends on the span, not on the choice of basis functions.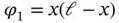 ,
, 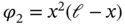 and show that the resulting approximate solution is identical to the approximate solution obtained in Example 1.1. The span of the basis functions in this exercise and in Example 1.1is the same: It is the set of polynomials of degree less than or equal to 3 that vanish in the points
and show that the resulting approximate solution is identical to the approximate solution obtained in Example 1.1. The span of the basis functions in this exercise and in Example 1.1is the same: It is the set of polynomials of degree less than or equal to 3 that vanish in the points 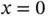 and
and 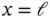 .
.










