Without a reliable estimate of the size of the numerical error it is not possible to certify design and, furthermore, numerical errors penalize design by lowering the allowable value, as indicated by eq. (1.4). Generally speaking, it is far more economical to ensure that τ is small than to accept the consequences of decreased allowable values.
We distinguish between finite element modeling and numerical simulation. As explained in greater detail in Chapter 5, finite element modeling evolved well before the theoretical basis of numerical simulation was developed. In finite element modeling a numerical problem is formulated by assembling elements from a library of finite elements that contains intuitively constructed beam, plate, shell, solid elements of various description. The numerical problem so created may not correspond to a well defined mathematical problem and therefore a solution may not even exist. For that reason it is not possible to speak of errors of approximation. Nevertheless, finite element modeling is widely practiced with success in some cases but with disappointing results in others. Such practice should be regarded as a practice of art, guided by intuition and experience, rather than a scientific activity. This is because practitioners of finite element modeling have to balance two kinds of very large errors: (a) conceptual errors in the formulation and (b) approximation errors in the numerical solution of an improperly posed mathematical problem.
In numerical simulation, on the other hand, the formulation of mathematical models is treated separately from their numerical solution. A mathematical model should be understood to be a precise statement of an idea of physical reality that permits the prediction of the occurrence, or probability of occurrence, of physical events, given certain data. The intuitive aspects of simulation are confined to the formulation of mathematical models whereas their numerical solution involves the application of well established procedures of applied mathematics. Separation of mathematical models from their numerical solution makes separate treatment of errors associated with the formulation of mathematical models and their numerical approximation possible. Errors associated with the formulation of mathematical models are called model form errors. Errors associated with the numerical solution of mathematical problems are called errors of approximation or errors of discretization. In the early papers and books on the finite element method no such distinction was made.
In this chapter we introduce the finite element method as a method by which the exact solution of a mathematical problem, cast in a generalized form, can be approximated. We also introduce the relevant mathematical concepts, terminology and notation in the simplest possible setting. Generalization of these concepts to two‐ and three‐dimensional problems will be discussed in subsequent chapters.
We first consider the formulation of a second order ordinary differential equation without reference to any physical interpretation. This is to underline that once a mathematical problem was formulated, the approximation process is independent from why the mathematical problem was formulated. This important point is often missed by engineering users of legacy finite element codes because the formulation and approximation of mathematical problems is mixed in finite element libraries.
We show that the exact solution of the generalized formulation is unique. Approximation of the exact solution by the finite element method is described and various discretization strategies are explored. Efficient methods for the computation of QoIs and a posteriori error estimation are described. This chapter serves as a foundation for subsequent chapters.
We would like to assure engineering students who are not yet familiar with the concepts and notation of that branch of applied mathematics on which the finite element method is based that their investment of time and effort to master the contents of this chapter will prove to be highly rewarding.
1.1 An introductory problem
We introduce the finite element method through approximating the exact solution of the following second order ordinary differential equation
(1.5) 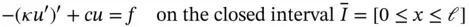
with the boundary conditions
(1.6) 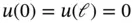
where the prime indicates differentiation with respect to x . It is assumed that 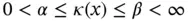 where α and β are real numbers,
where α and β are real numbers,  on
on 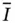 ,
, 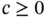 and
and 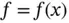 are defined such that the indicated operations are meaningful on I . For example, the indicated operations would not be meaningful if
are defined such that the indicated operations are meaningful on I . For example, the indicated operations would not be meaningful if 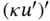 , c or f would not be finite in one or more points on the interval
, c or f would not be finite in one or more points on the interval 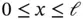 . The function f is called a forcing function.
. The function f is called a forcing function.
We seek an approximation to u in the form:
(1.7) 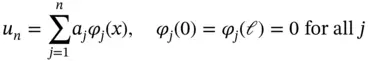
where 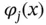 are fixed functions, called basis functions, and aj are the coefficients of the basis functions to be determined. Note that the basis functions satisfy the zero boundary conditions.
are fixed functions, called basis functions, and aj are the coefficients of the basis functions to be determined. Note that the basis functions satisfy the zero boundary conditions.
Let us find aj such that the integral 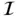 defined by
defined by
(1.8) 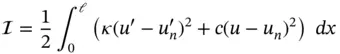
is minimum. While there are other plausible criteria for selecting aj , we will see that this criterion is fundamentally important in the finite element method. Differentiating 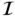 with respect to ai and letting the derivative equal to zero, we have:
with respect to ai and letting the derivative equal to zero, we have:
(1.9) 
Using the product rule: 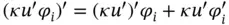 we write
we write
Читать дальше

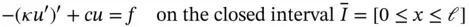
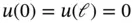
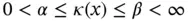 where α and β are real numbers,
where α and β are real numbers,  on
on 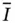 ,
, 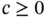 and
and 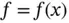 are defined such that the indicated operations are meaningful on I . For example, the indicated operations would not be meaningful if
are defined such that the indicated operations are meaningful on I . For example, the indicated operations would not be meaningful if 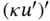 , c or f would not be finite in one or more points on the interval
, c or f would not be finite in one or more points on the interval 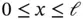 . The function f is called a forcing function.
. The function f is called a forcing function.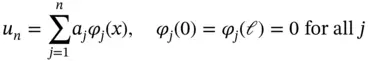
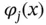 are fixed functions, called basis functions, and aj are the coefficients of the basis functions to be determined. Note that the basis functions satisfy the zero boundary conditions.
are fixed functions, called basis functions, and aj are the coefficients of the basis functions to be determined. Note that the basis functions satisfy the zero boundary conditions.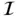 defined by
defined by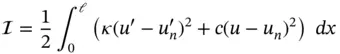
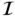 with respect to ai and letting the derivative equal to zero, we have:
with respect to ai and letting the derivative equal to zero, we have:
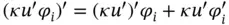 we write
we write










