1 ...7 8 9 11 12 13 ...36
Summary of the main points
1 The definition of the integral by eq. (1.8)made it possible to find an approximation to the exact solution u of eq. (1.5)without knowing u.
2 A formulation cannot be meaningful unless all indicated operations are defined. In the case of eq. (1.5)this means that and are finite on the interval . In the case of eq. (1.11)the integralmust be finite which is a much less stringent condition. In other words, eq. (1.8)is meaningful for a larger set of functions u than eq. (1.5)is. Equation (1.5)is the strong form, whereas eq. (1.11)is the generalized or weak form of the same differential equation. When the solution of eq. (1.5)exists then un converges to that solution in the sense that the limit of the integral is zero.
3 The error depends on the span and not on the choice of basis functions.
1.2 Generalized formulation
We have seen in the foregoing discussion that it is possible to approximate the exact solution u of eq. (1.5)without knowing u when 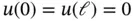 . In this section the formulation is outlined for other boundary conditions.
. In this section the formulation is outlined for other boundary conditions.
The generalized formulation outlined in this section is the most widely implemented formulation; however, it is only one of several possible formulations. It has the properties of stability and consistency. For a discussion on the requirements of stability and consistency in numerical approximation we refer to [5].
If eq. (1.5)holds then for an arbitrary function 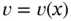 , subject only to the restriction that all of the operations indicated in the following are properly defined, we have
, subject only to the restriction that all of the operations indicated in the following are properly defined, we have
(1.17) 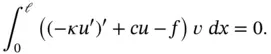
Using the product rule; 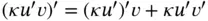 we get
we get
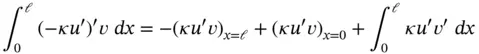
therefore eq. (1.17)is transformed to:
(1.18) 
We introduce the following notation:
(1.19) 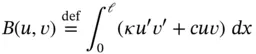
where 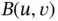 is a bilinear form. A bilinear form has the property that it is linear with respect to each of its two arguments. The properties of bilinear forms are listed Section A.1.3of Appendix A. We define the linear form:
is a bilinear form. A bilinear form has the property that it is linear with respect to each of its two arguments. The properties of bilinear forms are listed Section A.1.3of Appendix A. We define the linear form:
(1.20) 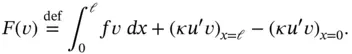
The forcing function 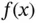 may be a sum of forcing functions:
may be a sum of forcing functions: 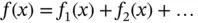 , some or all of which may be the Dirac delta function 4 multiplied by a constant. For example if
, some or all of which may be the Dirac delta function 4 multiplied by a constant. For example if 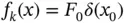 then
then
(1.21) 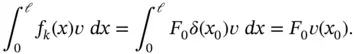
The properties of linear forms are listed in Section A.1.2. Note that 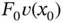 in eq. (1.21)is a linear form only if v is continuous and bounded.
in eq. (1.21)is a linear form only if v is continuous and bounded.
The definitions of 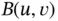 and
and 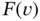 are modified depending on the boundary conditions. Before proceeding further we need the following definitions.
are modified depending on the boundary conditions. Before proceeding further we need the following definitions.
1 The energy norm is defined by(1.22) where I represents the open interval . This notation should be understood to mean that if and only if x satisfies the condition to the right of the bar (). This notation may be shortened to , or more generally where are real numbers. If the interval includes both boundary points then the interval is a closed interval denoted by .We have seen in the introductory example that the error is minimized in energy norm, that is, , equivalently is minimum. The square root is introduced so that (where α is a constant) holds. This is one of the definitive properties of norms listed in Section A.1.1.
2 The energy space, denoted by , is the set of all functions u defined on I that satisfy the following condition: (1.23)Since infinitely many linearly independent functions satisfy this condition, the energy space is infinite‐dimensional.
3 The trial space, denoted by , is a subspace of . When boundary conditions are prescribed on u, such as and/or , then the functions that lie in satisfy those boundary conditions. Note that when and/or then is not a linear space. This is because the condition stated under item 1 in Section A.1.1is not satisfied. When u is prescribed on a boundary then that boundary condition is called an essential boundary condition. If no essential boundary conditions are prescribed on u then .
4 The test space, denoted by , is a subspace of . When boundary conditions are prescribed on u, such as and/or then the functions that lie in are zero in those boundary points.If no boundary conditions are prescribed on u then . If is prescribed and is not known then(1.24) (1.25)If is not known and is prescribed then(1.26) (1.27) If and are prescribed then(1.28) (1.29)
We are now in a position to describe the generalized formulation for various boundary conditions in a concise manner;
1 When u is prescribed on a boundary then the boundary condition is called essential or Dirichlet 5 boundary condition. Let us assume that u is prescribed on both boundary points. In this case we write where is the function to be approximated and is an arbitrary fixed function that satisfies the boundary conditions. Substituting for u in eq. (1.18)we have:(1.30) and the generalized formulation is stated as follows: “Find such that for all ” where is defined by eq. (1.29). Note that is independent of the choice of . Essential boundary conditions are enforced by restriction on the space of admissible functions.
2 When is prescribed on a boundary then the boundary condition is called Neumann 6 boundary condition. Assume that and are prescribed. In this case(1.31) and the generalized formulation is: “Find such that for all ” where is defined by eq. (1.25).An important special case is when and and are prescribed. In this case:(1.32) and the generalized formulation is “Find such that for all where is defined by eq. (1.23).” Since the left‐hand side is zero for (constant) the specified data must satisfy the condition(1.33)
Читать дальше

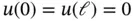 . In this section the formulation is outlined for other boundary conditions.
. In this section the formulation is outlined for other boundary conditions.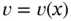 , subject only to the restriction that all of the operations indicated in the following are properly defined, we have
, subject only to the restriction that all of the operations indicated in the following are properly defined, we have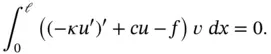
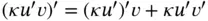 we get
we get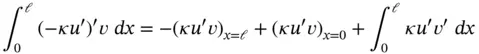

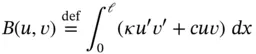
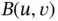 is a bilinear form. A bilinear form has the property that it is linear with respect to each of its two arguments. The properties of bilinear forms are listed Section A.1.3of Appendix A. We define the linear form:
is a bilinear form. A bilinear form has the property that it is linear with respect to each of its two arguments. The properties of bilinear forms are listed Section A.1.3of Appendix A. We define the linear form: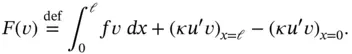
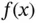 may be a sum of forcing functions:
may be a sum of forcing functions: 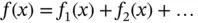 , some or all of which may be the Dirac delta function 4 multiplied by a constant. For example if
, some or all of which may be the Dirac delta function 4 multiplied by a constant. For example if 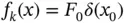 then
then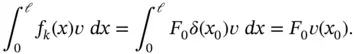
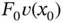 in eq. (1.21)is a linear form only if v is continuous and bounded.
in eq. (1.21)is a linear form only if v is continuous and bounded.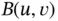 and
and 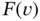 are modified depending on the boundary conditions. Before proceeding further we need the following definitions.
are modified depending on the boundary conditions. Before proceeding further we need the following definitions.










