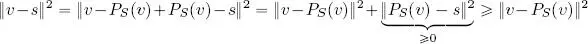
Figure 1.3. Visualization of property 2 in ℝ 2. For a color version of this figure, see www.iste.co.uk/provenzi/spaces.zip
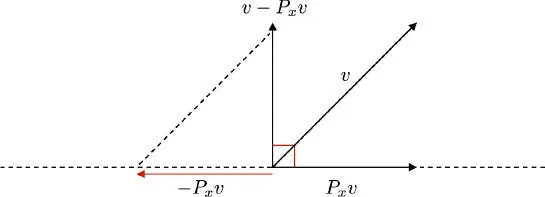
3) P x v minimizes the distance between the terminal point of v and the x axis. In Figure 1.2, 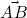 and
and 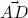 are, in fact, the hypotenuses of right-angled triangles ABC and ACD ; on the other hand,
are, in fact, the hypotenuses of right-angled triangles ABC and ACD ; on the other hand, 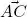 is another side of these triangles, and is therefore smaller than
is another side of these triangles, and is therefore smaller than 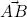 and
and 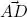 .
. 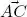 is the distance between the terminal point of v and the terminal point of P x v , while
is the distance between the terminal point of v and the terminal point of P x v , while 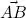 and
and 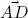 are the distances between the terminal point of v and the diagonal projections of v onto x rooted at B and D , respectively.
are the distances between the terminal point of v and the diagonal projections of v onto x rooted at B and D , respectively.
We wish to define an orthogonal projection operation for an abstract inner product space of dimension n which retains these same geometric properties.
Analyzing orthogonal projections in ℝ 3helps us to establish an idea of the algebraic definition of this operation. Figure 1.4shows a vector v ∈ ℝ 3and the plane produced by the orthogonal vectors u 1and u 2. We see that the projection p of v onto this plane is the vector sum of the orthogonal projections 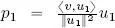 and
and  onto the two vectors u 1and u 2taken separately, i.e.
onto the two vectors u 1and u 2taken separately, i.e. 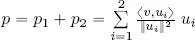 .
.
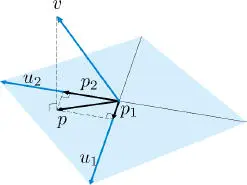
Figure 1.4. Orthogonal projection p of a vector in ℝ 3 onto the plane produced by two unit vectors. For a color version of this figure, see www.iste.co.uk/provenzi/spaces.zip
Generalization should now be straightforward: consider an inner product space ( V , 〈, 〉) of dimension n and an orthogonal family of non-zero vectors F = { u 1, . . . , u m}, m ≼ n , u i≠ 0 V∀ i = 1, . . . , m .
The vector subspace of V produced by all linear combinations of the vectors of F shall be written Span( F ):

The orthogonal projection operator or orthogonal projector of a vector v ∈ V onto S is defined as the following application, which is obviously linear:
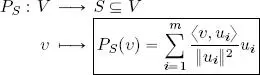
Theorem 1.12 shows that the orthogonal projection defined above retains all of the properties of the orthogonal projection demonstrated for ℝ 2.
THEOREM 1.12.– Using the same notation as before, we have:
1) if s ∈ S then P S( s ) = s , i.e. the action of P Son the vectors in S is the identity;
2) ∀ v ∈ V and s ∈ S , the residual vector of the projection, i.e. v − P S( v ), is ⊥ to S :
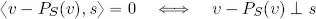
3) ∀ v ∈ V et s ∈ S : ‖ v − P S( v )‖ ≼ ‖ v − s ‖ and the equality holds if and only if s = P S( v ). We write:

PROOF.–
1) Let s ∈ S , i.e. 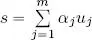 , then:
, then:
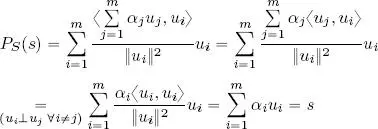
2) Consider the inner product of P S( v ) and a fixed vector u j, j ∈ {1, . . . , m }:
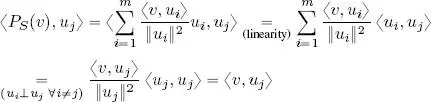
hence:
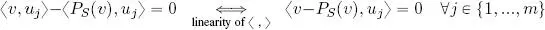
Lemma 1.1 guarantees that 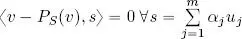 .
.
3) It is helpful to rewrite the difference v − s as v − P S( v ) + P S( v ) − s . From property 2, v − P S( v )⊥ S , however P S( v ), s ∈ S so P S( v )− s ∈ S . Hence ( v − P S( v )) ⊥ ( P S( v ) − s ). The generalized Pythagorean theorem implies that:
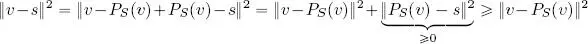
hence ‖ v − s ‖ ≽ ‖ v − P S( v )‖ ∀ v ∈ V, s ∈ S .
Evidently, ‖ P S( v ) − s ‖ 2= 0 if and only if s = P S( v ), and in this case ‖ v − s ‖ 2= ‖ v − P S( v )‖ 2.□
Читать дальше


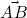 and
and 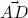 are, in fact, the hypotenuses of right-angled triangles ABC and ACD ; on the other hand,
are, in fact, the hypotenuses of right-angled triangles ABC and ACD ; on the other hand, 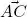 is another side of these triangles, and is therefore smaller than
is another side of these triangles, and is therefore smaller than 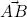 and
and 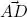 .
. 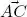 is the distance between the terminal point of v and the terminal point of P x v , while
is the distance between the terminal point of v and the terminal point of P x v , while 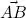 and
and 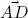 are the distances between the terminal point of v and the diagonal projections of v onto x rooted at B and D , respectively.
are the distances between the terminal point of v and the diagonal projections of v onto x rooted at B and D , respectively.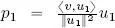 and
and  onto the two vectors u 1and u 2taken separately, i.e.
onto the two vectors u 1and u 2taken separately, i.e. 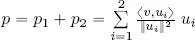 .
.

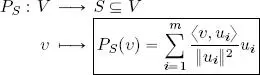
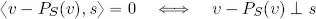

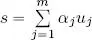 , then:
, then: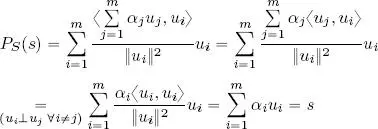
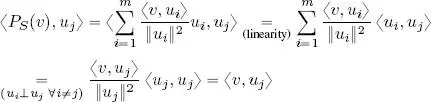
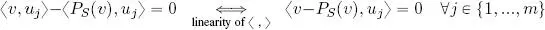
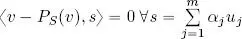 .
.