2) If ( u 1, . . . , u n) is an orthogonal, rather than an orthonormal, basis, then using the projector formula and theorem 1.12, the results of Theorem 1.14 can be written as:
a) decomposition of v ∈ V on an orthogonal basis :
[1.10] 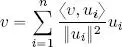
b) Parseval’s identity for an orthogonal basis :
[1.11] 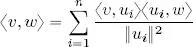
c) Plancherel’s theorem for an orthogonal basis :
[1.12] 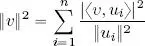
The following exercise is designed to test the reader’s knowledge of the theory of finite-dimensional inner product spaces. The two subsequent exercises explicitly include inner products which are non-Euclidean.
Exercise 1.1
Consider the complex Euclidean inner product space 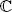 3and the following three vectors:
3and the following three vectors:
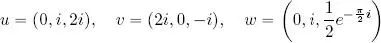
1) Determine the orthogonality relationships between vectors u, v, w .
2) Calculate the norm of u, v, w and the Euclidean distances between them.
3) Verify that ( u, v, w ) is a (non-orthogonal) basis of 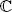 3.
3.
4) Let S be the vector subspace of 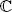 3generated by u and w . Calculate P S v , the orthogonal projection of v onto S . Calculate d ( v, P S v ), that is, the Euclidean distance between v and its projection onto S , and verify that this minimizes the distance between v and the vectors of S ( hint : look at the square of the distance).
3generated by u and w . Calculate P S v , the orthogonal projection of v onto S . Calculate d ( v, P S v ), that is, the Euclidean distance between v and its projection onto S , and verify that this minimizes the distance between v and the vectors of S ( hint : look at the square of the distance).
5) Using the results of the previous questions, determine an orthogonal basis and an orthonormal basis for 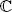 3without using the Gram-Schmidt orthonormalization process ( hint : remember the geometric relationship between the residual vector r and the subspace S ).
3without using the Gram-Schmidt orthonormalization process ( hint : remember the geometric relationship between the residual vector r and the subspace S ).
6) Given a vector a = (2 i , −1, 0), write the decomposition of a and Plancherel’s theorem in relation to the orthonormal basis identified in point 5. Use these results to identify the vector from the orthonormal basis which has the heaviest weight in the decomposition of a (and which gives the best “rough approximation” of a ). Use a graphics program to draw the progressive vector sum of a , beginning with the rough approximation and adding finer details supplied by the other vectors.
Solution to Exercise 1.1
1) Evidently, 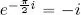 , so by directly calculating the inner products: 〈 u, v 〉 = −2, 〈 u, w 〉 = 0 et
, so by directly calculating the inner products: 〈 u, v 〉 = −2, 〈 u, w 〉 = 0 et 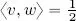 .
.
2) By direct calculation: 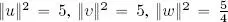 . After calculating the difference vectors, we obtain:
. After calculating the difference vectors, we obtain: 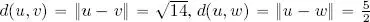 ,
, 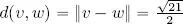 .
.
3) The three vectors u, v, w are linearly independent, so they form a basis in 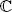 3. This basis is not orthogonal since only vectors u and w are orthogonal.
3. This basis is not orthogonal since only vectors u and w are orthogonal.
4) S = span( u, w ). Since ( u, w ) is an orthogonal basis in S , we can write:
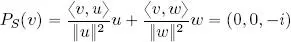
The residual vector of the projection of v on S is r = v − P S v = (2 i , 0, 0) and thus d ( v, P S v ) 2= ‖ r ‖ 2= 4. The most general vector in S is  and
and 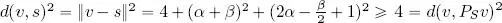 . This confirms that P S v is the vector in S with the minimum distance from v in relation to the Euclidean norm.
. This confirms that P S v is the vector in S with the minimum distance from v in relation to the Euclidean norm.
5) r is orthogonal to S , which is generated by u and w , hence ( u, w, r ) is a set of orthogonal vectors in 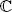 3, that is, an orthogonal basis of
3, that is, an orthogonal basis of 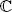 3. To obtain an orthonormal basis, we then simply divide each vector by its norm:
3. To obtain an orthonormal basis, we then simply divide each vector by its norm:
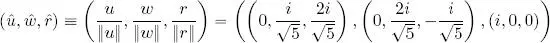
6) Decomposition:  .
.
Plancherel’s theorem: 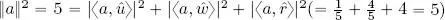 .
.
The vector with the heaviest weight in the reconstruction of a is thus r̂ : this vector gives the best rough approximation of a . By calculating the vector sum of this rough representation and the other two vectors, we can reconstruct the “fine details” of a , first with ŵ and then with û .
Exercise 1.2
Let M ( n , 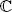 ) be the space of n × n complex matrices. The application ϕ : M ( n ,
) be the space of n × n complex matrices. The application ϕ : M ( n , 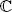 ) × M ( n ,
) × M ( n , 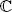 ) →
) → 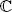 is defined by:
is defined by:
Читать дальше

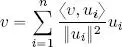
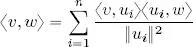
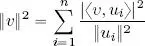
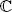 3and the following three vectors:
3and the following three vectors: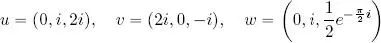
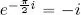 , so by directly calculating the inner products: 〈 u, v 〉 = −2, 〈 u, w 〉 = 0 et
, so by directly calculating the inner products: 〈 u, v 〉 = −2, 〈 u, w 〉 = 0 et 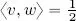 .
.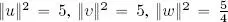 . After calculating the difference vectors, we obtain:
. After calculating the difference vectors, we obtain: 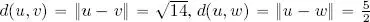 ,
, 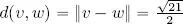 .
.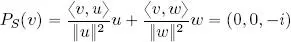
 and
and 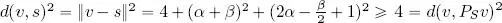 . This confirms that P S v is the vector in S with the minimum distance from v in relation to the Euclidean norm.
. This confirms that P S v is the vector in S with the minimum distance from v in relation to the Euclidean norm.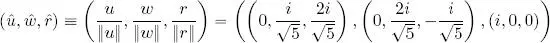
 .
.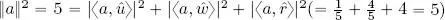 .
.










