1.3. Orthogonal and orthonormal families in inner product spaces
The “geometric” definition of an inner product in ℝ 2and ℝ 3indicates that this product is zero if and only if ϑ , the angle between the vectors, is π /2, which implies cos( ϑ ) = 0.
In more complicated vector spaces (e.g. polynomial spaces), or even Euclidean vector spaces of more than three dimensions, it is no longer possible to visualize vectors; their orthogonality must therefore be “axiomatized” via the nullity of their scalar product.
DEFINITION 1.5.– Let ( V , 〈, 〉) be a real or complex inner product space of finite dimension n. Let F = { v 1, · · · , v n} be a family of vectors in V . Thus:
– F is an orthogonal family of vectors if each different vector pair has an inner product of 0: 〈 v i, v j〉 = 0 ;
– F is an orthonormal family if it is orthogonal and, furthermore , ‖ v i‖ = 1 ∀ i. Thus, if 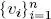 is an orthogonal family ,
is an orthogonal family , 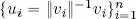 is an orthonormal family.
is an orthonormal family.
An orthonormal family (unit and orthogonal vectors) may be characterized as follows:
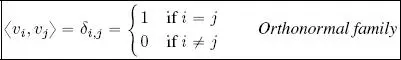
δ i,jis the Kronecker delta 5.
1.4. Generalized Pythagorean theorem
The Pythagorean theorem can be generalized to abstract inner product spaces. The general formulation of this theorem is obtained using a lemma.
LEMMA 1.1.– Let ( V , 〈, 〉) be a real or complex inner product space. Let u ∈ V be orthogonal to all vectors v 1, . . . , v n∈ V . Hence, u is also orthogonal to all vectors in V obtained as a linear combination of v 1, . . . , v n.
PROOF.– Let 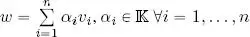 , be an arbitrary linear combination of vectors v 1, . . . , v n. By direct calculation:
, be an arbitrary linear combination of vectors v 1, . . . , v n. By direct calculation:
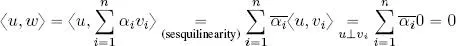 □
□
THEOREM 1.8 (Generalized Pythagorean theorem).– Let ( V , 〈, 〉) be an inner product space on  . Let u, v ∈ V be orthogonal to each other. Hence:
. Let u, v ∈ V be orthogonal to each other. Hence:
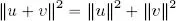
More generally, if the vectors v 1,. . . , v n∈ V are orthogonal, then:
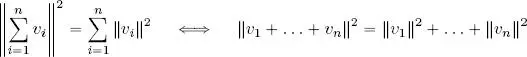
PROOF.– The two-vector case can be proven thanks to Carnot’s formula:
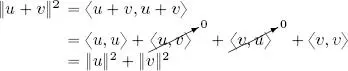
Proof for cases with n vectors is obtained by recursion:
– the case where n = 2 is demonstrated above;
– we suppose that 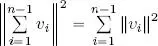 (recursion hypothesis);
(recursion hypothesis);
– now, we write u = v nand 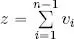 , so u ⊥ z using Lemma 1.1. Hence, using case n = 2: ‖ u + z ‖ 2= ‖ u ‖ 2+ ‖ z ‖ 2, but:
, so u ⊥ z using Lemma 1.1. Hence, using case n = 2: ‖ u + z ‖ 2= ‖ u ‖ 2+ ‖ z ‖ 2, but:
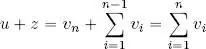
so:
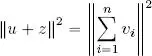
and:

giving us the desired thesis.
Note that the Pythagorean theorem thesis is a double implication if and only if V is real , in fact, using law [ 1.6] we have that ‖ u + v ‖ 2= ‖ u ‖ 2+ ‖ v ‖ 2holds true if and only if ℜ(〈 u, v 〉) = 0, which is equivalent to orthogonality if and only if V is real.
The following result gives information concerning the distance between any two vectors within an orthonormal family.
THEOREM 1.9.– Let ( V , 〈, 〉) be an inner product space on 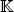 and let F be an orthonormal family in V . The distance between any two elements of F is constant and equal to
and let F be an orthonormal family in V . The distance between any two elements of F is constant and equal to 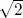 .
.
PROOF.– Using the Pythagorean theorem: ‖ u + (− v )‖ 2= ‖ u ‖ 2+ ‖ v ‖ 2= 2, from the fact that u ⊥ v .□
1.5. Orthogonality and linear independence
The orthogonality condition is more restrictive than that of linear independence: all orthogonal families are free .
THEOREM 1.10.– Let F be an orthogonal family in ( V , 〈, 〉), F = { v 1, · · · , v n}, v i≠ 0 ∀ i , then F is free.
PROOF.– We need to prove the linear independence of the elements v i, that is,  . To this end, we calculate the inner product of the linear combination
. To this end, we calculate the inner product of the linear combination 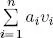 and an arbitrary vector v jwith j ∈ {1, . . . , n }:
and an arbitrary vector v jwith j ∈ {1, . . . , n }:
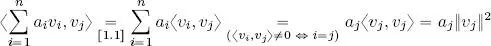
By hypothesis, none of the vectors in F are zero; the hypothesis that 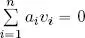 therefore implies that:
therefore implies that:
Читать дальше

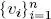 is an orthogonal family ,
is an orthogonal family , 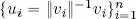 is an orthonormal family.
is an orthonormal family.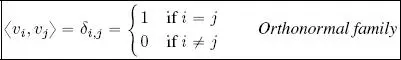
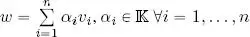 , be an arbitrary linear combination of vectors v 1, . . . , v n. By direct calculation:
, be an arbitrary linear combination of vectors v 1, . . . , v n. By direct calculation: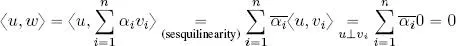 □
□ . Let u, v ∈ V be orthogonal to each other. Hence:
. Let u, v ∈ V be orthogonal to each other. Hence: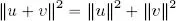
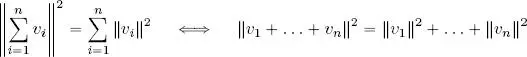
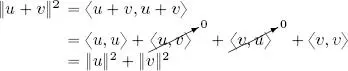
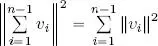 (recursion hypothesis);
(recursion hypothesis);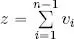 , so u ⊥ z using Lemma 1.1. Hence, using case n = 2: ‖ u + z ‖ 2= ‖ u ‖ 2+ ‖ z ‖ 2, but:
, so u ⊥ z using Lemma 1.1. Hence, using case n = 2: ‖ u + z ‖ 2= ‖ u ‖ 2+ ‖ z ‖ 2, but: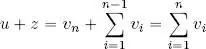
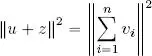

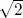 .
. . To this end, we calculate the inner product of the linear combination
. To this end, we calculate the inner product of the linear combination 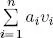 and an arbitrary vector v jwith j ∈ {1, . . . , n }:
and an arbitrary vector v jwith j ∈ {1, . . . , n }: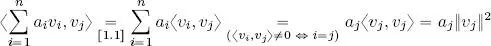
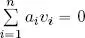 therefore implies that:
therefore implies that:










