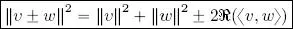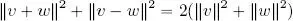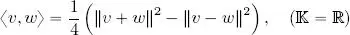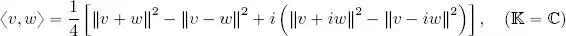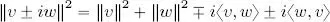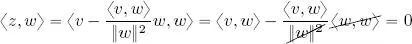
thus:
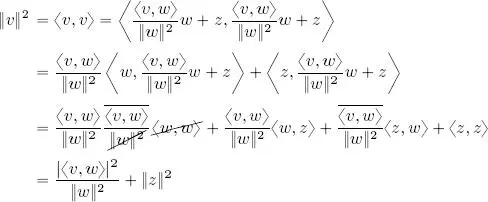
as the two intermediate terms in the penultimate step are zero, since 〈 z, w 〉 = 〈 w, z 〉 = 0.
As ‖ z ‖ 2≽ 0, we have seen that:
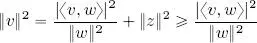
i.e. |〈 v, w 〉| 2≼ ‖ v ‖ 2‖ w ‖ 2, hence |〈 v, w 〉| ≼ ‖ v ‖‖ w ‖;
– second proof (in one line!): ∀ t ∈ ℝ we have:
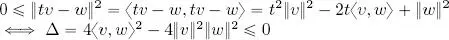
The Cauchy-Schwarz inequality allows the concept of the angle between two vectors to be generalized for abstract vector spaces. In fact, it implies the existence of a coefficient k between −1 and +1 such that 〈 v, w 〉 = ‖ v ‖‖ w ‖ k , but, given that the restriction of cos to [0, π ] creates a bijection with [−1, 1], this means that there is only one ϑ ∈ [0, π ] such that 〈 v, w 〉 = ‖ v ‖‖ w ‖ cos ϑ . ϑ ∈ [0, π ] is known as the angle between the two vectors v and w .
Another very important property of the norm is as follows.
THEOREM 1.4.– Let ( V , ‖ ‖) be an arbitrary normed vector space and v, w ∈ V . We have:
[1.3] 
PROOF.– On one side:
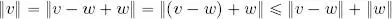
by the triangle inequality, thus ‖ v ‖ − ‖ w ‖ ≼ ‖ v − w ‖. On the other side:
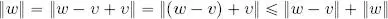
thus ‖ w ‖ − ‖ v ‖ ≼ ‖ v − w ‖, i.e. ‖ v ‖ − ‖ w ‖ ≽ − ‖ v − w ‖.
Hence, −‖ v − w ‖ ≼ ‖ v ‖ − ‖ w ‖ ≼ ‖ v − w ‖, i.e. |‖ v ‖ − ‖ w ‖| ≼ ‖ v − w ‖.
The following formula is also extremely useful.
THEOREM 1.5 (Carnot’s theorem).– Taking v, w ∈ ( V , 〈 , 〉):
[1.4] 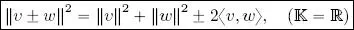
and
[1.5] 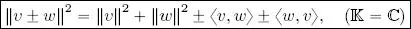
PROOF.– Direct calculation:
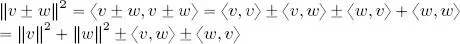
If  =
=  , then
, then  , and since, if z = a + ib = ℜ ( z ) + i ℑ( z ), then z +
, and since, if z = a + ib = ℜ ( z ) + i ℑ( z ), then z +  = 2 a = 2ℜ( z ), we can rewrite [ 1.5] as:
= 2 a = 2ℜ( z ), we can rewrite [ 1.5] as:
[1.6] 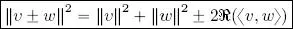
The laws presented in this section have immediate consequences which will be highlighted in section 1.2.1.
1.2.1. The parallelogram law and the polarization formula
The parallelogram law in ℝ 2is shown in Figure 1.1. This law can be generalized on a vector space with an arbitrary inner product.
THEOREM 1.6 (Parallelogram law).– Let ( V , 〈, 〉) be an inner product space on  . Thus, ∀ v, w ∈ V :
. Thus, ∀ v, w ∈ V :
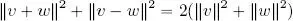
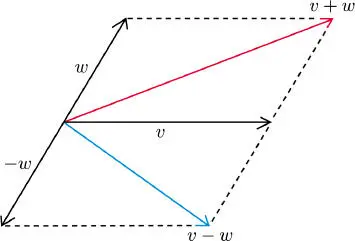
Figure 1.1. Parallelogram law in ℝ 2 : The sum of the squares of the two diagonal lines is equal to two times the sum of the squares of the edges v and w. For a color version of this figure, see www.iste.co.uk/provenzi/spaces.zip
PROOF.– A direct consequence of law [ 1.4] or law [ 1.5] taking ‖ v + w ‖ 2then ‖ v − w ‖ 2.
□
As we have seen, an inner product induces a norm. The polarization formula can be used to “reverse” roles and write the inner product using the norm.
THEOREM 1.7 (Polarization formula).– Let ( V , 〈, 〉) be an inner product space on 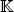 . In this case, ∀ v, w ∈ V :
. In this case, ∀ v, w ∈ V :
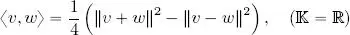
and:
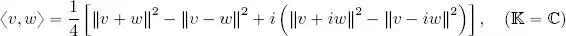
PROOF.– This law is a direct consequence of law [ 1.4], in the real case. For the complex case, w is replaced by iw in law [ 1.5], and by sesquilinearity, we obtain:
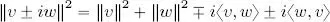
By direct calculation, we can then verify that ‖ v + w ‖ 2− ‖ v − w ‖ 2+ i ‖ v + iw ‖ 2− i ‖ v − iw ‖ 2= 4〈 v, w 〉.
It may seem surprising that something as simple as the parallelogram law may be used to establish a necessary and sufficient condition to guarantee that a norm over a vector space will be induced by an inner product, that is, the norm is Hilbertian. This notion will be formalized in Chapter 4.
Читать дальше

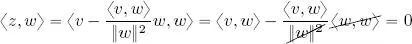
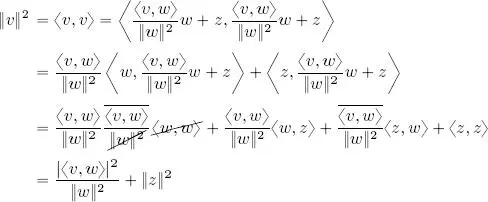
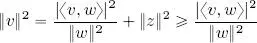
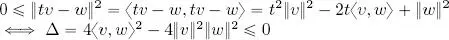

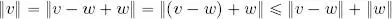
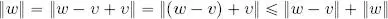
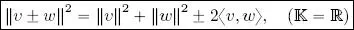
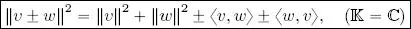
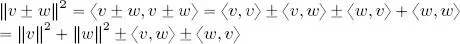
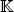 =
= 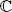 , then
, then  , and since, if z = a + ib = ℜ ( z ) + i ℑ( z ), then z +
, and since, if z = a + ib = ℜ ( z ) + i ℑ( z ), then z +  = 2 a = 2ℜ( z ), we can rewrite [ 1.5] as:
= 2 a = 2ℜ( z ), we can rewrite [ 1.5] as: