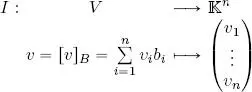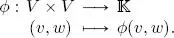From this perspective, the theory of Hilbert spaces may be seen as an elegant conjunction of algebra, analysis and topology. It draws on the work of some of the great mathematicians of the early 20th century, including Riesz, Banach and, evidently, Hilbert, who established the conditions needed to extend classical algebra and analysis into infinite dimensions.
One particularly important linear operator, the Fourier transform, appears on multiple occasions throughout this book. We start by examining the properties of this transform in finite dimensions, with the discrete Fourier transform, before extending it to infinite dimensions, considering the use of this operator in a range of different domains, including signal and image processing.
A clear understanding of the concepts introduced in this book is essential for mathematicians, physicists or engineers hoping to progress in any field, whether applied or theoretical. These concepts provide access to tools and techniques developed over a particularly rich, creative period in the history of mathematics, which remain relevant for both pure and applied forms of the subject.
The author would like to thank Olivier Husson for his assistance in producing the majority of the figures included in this book.
April 2021
1
Inner Product Spaces (Pre-Hilbert)
This chapter will focus on inner product spaces, that is, vector spaces with a scalar product, specifically those of finite dimension .
1.1. Real and complex inner products
In real Euclidean spaces ℝ 2and ℝ 3, the inner product of two vectors v, w is defined as the real number:

where ϑ is the smallest angle between v and w and ‖ ‖ represents the norm (or the magnitude) of the vectors.
Using the inner product, it is possible to define the orthogonal projection of vector v in the direction defined by vector w . A distinction must be made between:
1 – the scalar projection of v in the direction of ; and
2 – the vector projection of v in the direction of ;
where 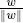 is the unit vector in the direction of w . Evidently, the roles of v and w can be reversed.
is the unit vector in the direction of w . Evidently, the roles of v and w can be reversed.
The absolute value of the scalar projection measures the “similarity” of the directions of two vectors . To understand this concept, consider two remarkable relative positions between v and w :
1 – if v and w possess the same direction, then the angle between them ϑ is either null or π, hence cos(ϑ) = ±1, that is, the absolute value of the scalar projection of v in direction w is ‖v‖;
2 – however, if v and w are perpendicular, then and hence cos(ϑ) = 0, showing that the scalar projection of v in direction w is null.
When the position of v relative to w falls somewhere in the interval between the two vectors described above, the absolute value of the scalar projection of v in the direction of w falls between 0 and ‖ v ‖; this explains its use to measure the similarity of the direction of vectors.
In this book, we shall consider vector spaces which are far more complex than ℝ 2and ℝ 3, and the measure of vector similarity obtained through projection supplies crucial information concerning the coherence of directions.
Before we can obtain this information, we must begin by moving from Euclidean spaces ℝ 2and ℝ 3to abstract vector spaces. The general definition of an inner product and an orthogonal projection in these spaces may be seen as an extension of the previous definitions, permitting their application to spaces in which our representation of vectors is no longer applicable.
Geometric properties, which can only be apprehended and, notably, visualized in two or three dimensions, must be replaced by a set of algebraic properties which can be used in any dimension.
Evidently, these algebraic properties must be necessary and sufficient to characterize the inner product of vectors in a plane or in real space. This approach, in which we generalize concepts which are “intuitive” in two or three dimensions, is a classic approach in mathematics.
In this chapter, the symbol V will be used to describe a vector space defined over the field 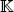 , where
, where 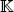 is either ℝ or
is either ℝ or 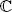 and is of finite dimension n < +∞. field
and is of finite dimension n < +∞. field 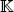 contains the scalars used to construct linear combinations between vectors in V . Note that two finite dimensional vector spaces are isomorphic if and only if they are of the same dimension. Furthermore, if we establish a basis B = ( b 1, . . . , b n) for V , an isomorphism between V and
contains the scalars used to construct linear combinations between vectors in V . Note that two finite dimensional vector spaces are isomorphic if and only if they are of the same dimension. Furthermore, if we establish a basis B = ( b 1, . . . , b n) for V , an isomorphism between V and 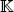 ncan be constructed as follows:
ncan be constructed as follows:
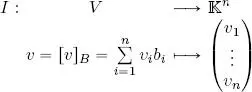
that is, I associates each v ∈ V with the vector of 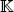 ngiven by the scalar components of v in relation to the established basis B . Since I is an isomorphism, it follows that
ngiven by the scalar components of v in relation to the established basis B . Since I is an isomorphism, it follows that 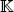 n is the prototype of all vector spaces of dimension n over a field
n is the prototype of all vector spaces of dimension n over a field 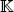 .
.
DEFINITION 1.1.– Let V be a vector space defined over a field 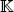 .
.
A 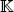 -form over V is an application defined over V × V with values in
-form over V is an application defined over V × V with values in 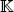 , that is:
, that is:
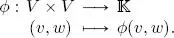
DEFINITION 1.2.– Let V be a real vector space. A couple ( V , 〈, 〉) is said to be a real inner product space (or a real pre-Hilbert space) if the form 〈, 〉 is:
1) bilinear, i.e.1 linear in relation to each argument (the other being fixed):
Читать дальше


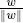 is the unit vector in the direction of w . Evidently, the roles of v and w can be reversed.
is the unit vector in the direction of w . Evidently, the roles of v and w can be reversed.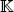 , where
, where 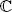 and is of finite dimension n < +∞. field
and is of finite dimension n < +∞. field