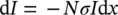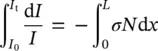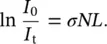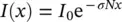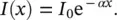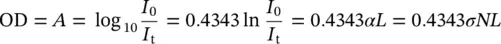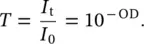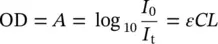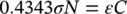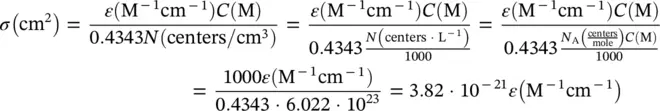Spectroscopy for Materials Characterization

An introductory experiment that highlights the effect of absorption of light is represented in Figure 1.1.

A parallel beam of lightwave with wavelength λ and intensity I 0( λ ) impinges perpendicularly on a face of a parallelepiped specimen of matter. It is useful to recall that λ and ν are connected by the speed of light c (2.9979 × 10 8m⋅s −1in vacuum): λ = c / ν [1]. Passing through the sample, the light intensity could be reduced, and at the exit, the amount I measured at λ could be diminished to the value I t( λ ) [2–4]. The eventual intensity reduction inside the specimen increases continuously on increasing the size L . If a portion of thickness d x of the sample is considered, it is expected that passing through it, I decreases by a quantity d I (for simplicity, λ will be omitted henceforth). This effect depends on the presence of absorbing centers in the volume considered, on the one side, and on their physical properties, on the other. These features are taken into account by the concentration of centers, N , and by their cross section, σ . Larger is the concentration of centers, larger absorption will take place. On increasing the probability of radiation–matter interaction, σ increases too, as well as the absorption effect. If a homogeneous and isotropic distribution of absorbing centers inside the volume of the sample is considered, it can be assumed that [3]:

(1.1)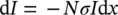

where the units are J (cm 2⋅s) −1for I , centers cm −3for N , cm 2for σ, and cm for d x . By considering the entire sample, Eq. (1.1)can be integrated to obtain:

(1.2)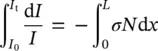

and determine the solution

(1.3)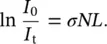

In general, from solution (1.3), it is found that at a position x inside the sample

(1.4)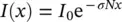

this is the Lambert–Beer law that expresses the attenuation of light intensity as a function of the thickness of the sample traversed [2, 3]. A typical expected profile of light intensity in traversing a sample is reported in Figure 1.1. It is useful to introduce some quantities commonly associated to the absorption effect. The empirical one is the absorption coefficient defined by the experimental macroscopic measurement of attenuation:

(1.5)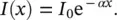

It is easy to show that α = σN , connecting the macroscopic quantities α and N to the microscopic one σ (see Section 1.2to find the relation to atomic and molecular properties). Then, we report the instrumental quantity, the optical density (OD), also called absorbance ( A ) [5, 6]:

(1.6)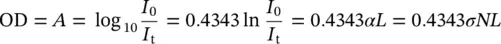

and the transmittance , T :

(1.7)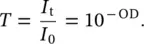

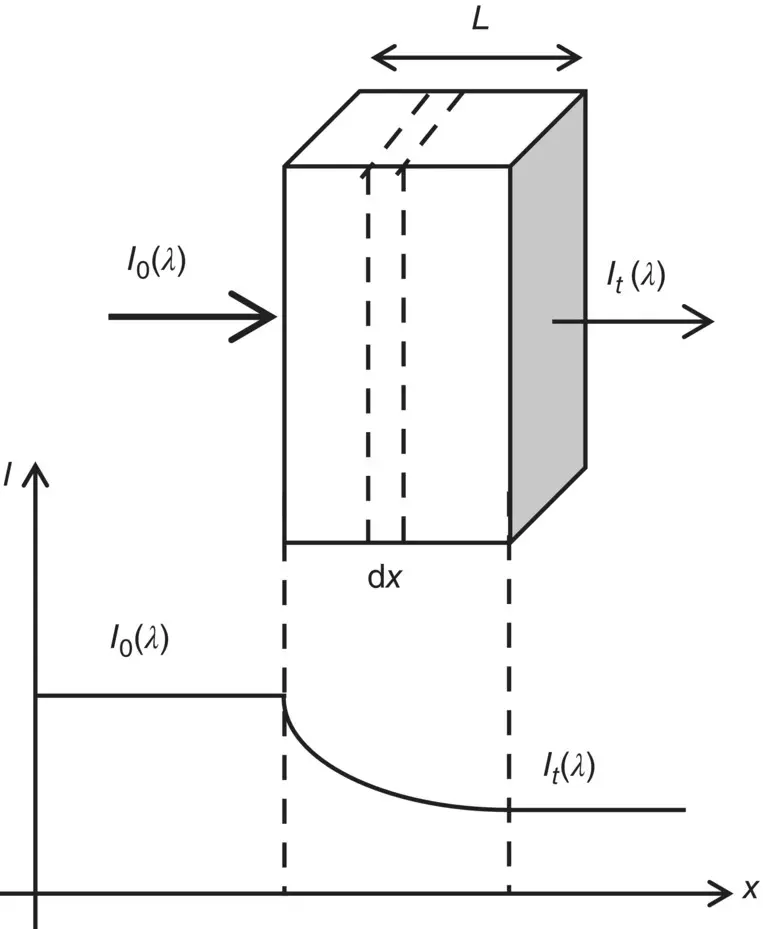
Figure 1.1Schematic representation of a beam of light at wavelength λ passing through a parallelepiped of matter. In the bottom, the qualitative decrease of intensity is reported. I 0is the impinging intensity and I tthe transmitted one.

It is worth noting that when OD ≪ 1, 1 − T = 1 − 10 −OD≈ 1 − (1 − OD) = OD = A , so the absorbance and the optical density can be derived directly from the transmittance [6]. Finally, it is also useful to introduce a quite diffuse alternative to Eq. (1.6):

(1.8)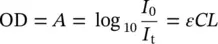

where ε is the molar extinction coefficient , or molar absorption coefficient , having units liter/(mole⋅cm) [M −1⋅cm −1], and C is the concentration of absorbing centers, in mole/liter [M]. By equating (1.6)and (1.8), it is shown that

(1.9)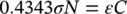

having used centers cm −3for N and cm 2for σ . Then, considering the Avogadro’s number, N A= 6.022 10 23centers mole −1, we obtain the conversion formula

(1.10)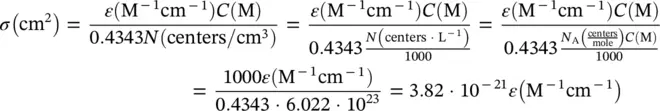

these quantities are related to the electronic states of absorbing centers, as will be shown later.

Concluding, the Lambert–Beer law states that the optical density is proportional to the concentration of absorbing centers and to their electronic properties. All of the above considerations can be extended to any λ and the study of absorption as a function of the wavelength impinging on the sample gives origin to the absorption spectrum.

It is worth noting that some physical phenomena can influence the experimental evaluation of the optical density. The light scattering (both elastic process, Rayleigh scattering, and anelastic process, Raman scattering [7, 8]) can deviate the beam and avoid its exit in the detection direction. This effect could give origin to an inexact estimate of OD and can be evidenced by a λ −4background dependence of absorbance [1, 7]. In particular, it could be erroneously concluded that photons have been absorbed whereas only their path has been deviated by the matter without any energy transfer from the electromagnetic field to the atoms. A second physical effect is the emission of light from the sample caused by the return of the electron to its thermal equilibrium state after the absorption phenomenon, promoting it to an excited state (see further). The emission is usually at a wavelength different to the impinging one, but if the light exiting from the sample is not recorded identifying the λ , as usually done in a single monochromator spectrometer, a wrong estimate of the optical density can be done. The latter effect could be relevant if absorption is large and photons of impinging light are highly reduced in number through the sample and the exiting counted photons mainly coincide with those emitted. The latter effect can be instrumentally avoided by using a double monochromator setup. Neglecting instrumental effects like stray light, that is parasitic light arriving at the detector not passing through the sample, and signal‐to‐noise limits [2, 3], another physical effect to be taken into account is reflection [1, 4]. When the parallel beam reported in Figure 1.1impinges perpendicularly on the sample surface, the mismatch of refractive index between the medium ( n 1) and the sample ( n 2) induces a transmitted and a reflected beam [1, 4]. Introducing the reflectivity r for normal incidence of light: