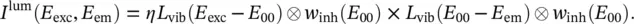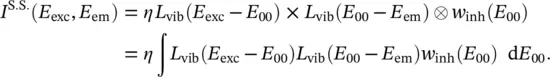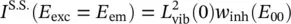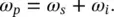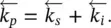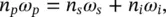where E 00is the energy of the ZPL and  is the Huang–Rhys factor associated with the localized mode. The inhomogeneity arises from the site‐to‐site nonequivalence of defects embedded in the amorphous network. It is well‐founded to assume that only the ZPL features a statistical distribution w inh( E 00); the total absorption lineshape, I abs( E exc), is therefore given by the convolution:
is the Huang–Rhys factor associated with the localized mode. The inhomogeneity arises from the site‐to‐site nonequivalence of defects embedded in the amorphous network. It is well‐founded to assume that only the ZPL features a statistical distribution w inh( E 00); the total absorption lineshape, I abs( E exc), is therefore given by the convolution:
(2.68) 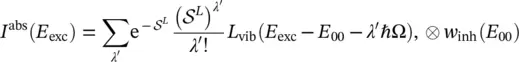
that makes explicit the dependence on the microscopic parameters ( E 00, 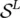 , ℏΩ) in Eq. (2.57). Similarly, the luminescence lineshape is the convolution between a homogeneous function, which is mirror‐symmetric of
, ℏΩ) in Eq. (2.57). Similarly, the luminescence lineshape is the convolution between a homogeneous function, which is mirror‐symmetric of 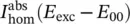 against E 00, and the inhomogeneous distribution w inh( E 00), while its amplitude is proportional to the absorbed intensity, scaled by the quantum yield factor η ≤ 1:
against E 00, and the inhomogeneous distribution w inh( E 00), while its amplitude is proportional to the absorbed intensity, scaled by the quantum yield factor η ≤ 1:
(2.69) 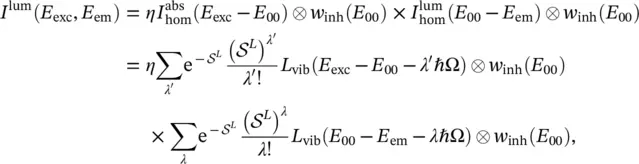
that reproduces the lineshape function appearing in Eq. (2.63).
The attempt to single out homogeneous and inhomogeneous lineshapes by site‐selective luminescence is successful only for a peculiar subclass of defects having a very low electron–phonon coupling ( 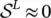 ). In this case, Eq. (2.69)becomes:
). In this case, Eq. (2.69)becomes:
(2.70) 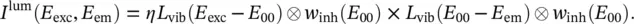
Under this condition, absorption and luminescence spectra overlap and the ZPL lies in this region. It is, therefore, possible to site‐selectively excite a specific defect subset within w inh( E 00); the site‐selective luminescence intensity is given by:
(2.71) 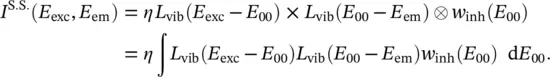
At low temperature, L vib( E exc− E 00) as well as L vib( E 00− E em) vanish for negative arguments, so that the site‐selective luminescence is detected with the emission resonant to excitation, E E ex= E em, namely the ZPL, and Eq. (2.71)reduces to:
(2.72) 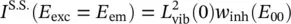
thus allowing the measure of the inhomogeneous distribution w inh( E 00).
2.2.3 Basic Design of Experimental Setup: Pulsed Laser Sources; Monochromators; Detectors
In this section, we describe a typical setup that can be conveniently used to perform time‐resolved photoluminescence measurements. The main components of the experimental station are: an integrated Tunable Laser System , a Spectrograph , an Intensified CCD Camera .
The tunable laser is an integrated system that provides the excitation radiation with a wavelength that can be conveniently adjusted within a wide spectral range covering UV‐Visible‐IR. A very common example exploits the third harmonic of a Q‐switched Nd:YAG laser (355 nm) to pump an optical parametric oscillator (OPO) that converts it into a tunable output.
The laser active medium is a crystal of yttrium‐aluminum‐garnet (YAG) doped with Nd 3+ions, which is pumped by a flashed Xenon lamp via the ∼800 nm Nd 3+absorption transition. The Q‐switching is triggered by an electro‐optic crystal (Pockel cell, PC) placed within the laser cavity. When the PC is not polarized, the cavity Q ‐factor is low and the population inversion is high without any laser oscillations. When the PC is polarized, the Q ‐factor suddenly increases and the laser action starts with a strong initial inversion, thus resulting in the buildup of an intense pulse (~10 2mJ, ~5 ns long).
The laser beam at λ 0= 1064 nm (fundamental harmonic) produced by the Nd:YAG laser is directed on a second harmonic generator (SHG), where the wavelength is converted to λ 0/2 = 532 nm, and then on a third harmonic generator (THG), where it is converted to λ 0/3 = 355 nm. The SHG and THG are nonlinear KD*P (KH 2PO 4) birefringent crystals, cut at the proper angle for the required wavelength. The nonlinear conversion process critically depends on the relative orientation of the polarization axis of the incident beam and the axes of the nonlinear crystals. The maximum efficiency is obtained when the phase matching is verified; it requires that the phase velocities of the frequency‐doubled and the incident waves are the same within the crystal.
Then, the third harmonic of frequency ω ptraverses the OPO, a birefringent nonlinear BBO ( β ‐BaB 2O 4) crystal, and is converted into two beams, signal and idler , with frequencies ω sand ω i, respectively. Because of the energy conservation, the following condition applies:
(2.73) 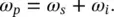
To achieve the phase matching condition within the OPO, the conservation of momentum has to be fulfilled as well:
(2.74) 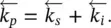
The previous equation can be written in the form:
(2.75) 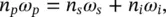
where n p, n s, and n iare the refractive indices of the nonlinear crystal at the frequencies ω p, ω s, and ω i, respectively. Since the refractive index depends on the polarization of the light and the angle of incidence with respect to the optical axis of the BBO crystal, the OPO output can be thus continuously tuned over a wide spectral range by varying the crystal orientation. The idler polarization is perpendicular to the optical bench while the signal polarization is parallel; then a polarizer is placed in front of the OPO to select one of them. Usually, the signal wavelength can be varied from 410 to 710 nm and the idler wavelength from 710 to 2400 nm. Moreover, the output wavelength range can be extended down to 210 nm by suitable UV modules, SHG nonlinear crystals, that halve the wavelength of the OPO beam. In such tunable laser systems, the beam intensity can reach tens of mJ pulse −1, the linewidth is ~1 meV.
Читать дальше

 is the Huang–Rhys factor associated with the localized mode. The inhomogeneity arises from the site‐to‐site nonequivalence of defects embedded in the amorphous network. It is well‐founded to assume that only the ZPL features a statistical distribution w inh( E 00); the total absorption lineshape, I abs( E exc), is therefore given by the convolution:
is the Huang–Rhys factor associated with the localized mode. The inhomogeneity arises from the site‐to‐site nonequivalence of defects embedded in the amorphous network. It is well‐founded to assume that only the ZPL features a statistical distribution w inh( E 00); the total absorption lineshape, I abs( E exc), is therefore given by the convolution: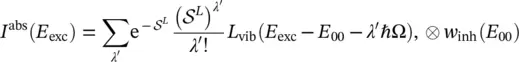
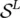 , ℏΩ) in Eq. (2.57). Similarly, the luminescence lineshape is the convolution between a homogeneous function, which is mirror‐symmetric of
, ℏΩ) in Eq. (2.57). Similarly, the luminescence lineshape is the convolution between a homogeneous function, which is mirror‐symmetric of 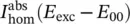 against E 00, and the inhomogeneous distribution w inh( E 00), while its amplitude is proportional to the absorbed intensity, scaled by the quantum yield factor η ≤ 1:
against E 00, and the inhomogeneous distribution w inh( E 00), while its amplitude is proportional to the absorbed intensity, scaled by the quantum yield factor η ≤ 1: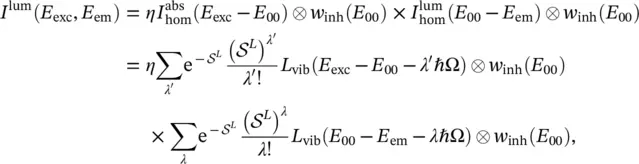
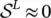 ). In this case, Eq. (2.69)becomes:
). In this case, Eq. (2.69)becomes: