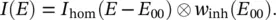Source: Modified from Skuja [11].
I and II are the electronic states, λ and λ ′denote the localized vibration, n sand m sare the sets of the band vibrations, 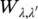 is the transition probability between the localized vibration levels in the ground and excited electronic states, and
is the transition probability between the localized vibration levels in the ground and excited electronic states, and 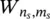 is the transition probability between the band vibration levels. In the approximation kT ≪ ℏΩ, λ = 0 and the previous equation averaged over the band vibration states is:
is the transition probability between the band vibration levels. In the approximation kT ≪ ℏΩ, λ = 0 and the previous equation averaged over the band vibration states is:
(2.50) 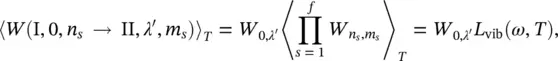
where ω is the frequency of the transition n s→ m s.
Equations (2.49)and (2.50)determine the spectral features of the whole optical band. The intensity of transitions coupled to the localized vibration going from λ = 0 to λ ′( λ ′= 0, 1, 2…), 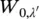 , is not influenced by the interaction with the band vibrations so that is distributed according to the Poisson distribution of Eq. (2.48). The band vibrations, in turn, give rise to an internal lineshape, L vib( ω , T ) ,featuring the properties of the vibronic band in the absence of a localized vibration: a ZPL and a vibrational background. Upon increasing temperature, the ZPL intensity decreases and the vibrational background increases so that the total intensity remains constant. L vib( ω , T ) follows a similarity law : the overall spectrum is a series of replicas of vibronic lines spaced apart by λ ′Ω ( λ ′= 0,1,2, …) from the electronic transition. The intensity of each replica is given by the factor
, is not influenced by the interaction with the band vibrations so that is distributed according to the Poisson distribution of Eq. (2.48). The band vibrations, in turn, give rise to an internal lineshape, L vib( ω , T ) ,featuring the properties of the vibronic band in the absence of a localized vibration: a ZPL and a vibrational background. Upon increasing temperature, the ZPL intensity decreases and the vibrational background increases so that the total intensity remains constant. L vib( ω , T ) follows a similarity law : the overall spectrum is a series of replicas of vibronic lines spaced apart by λ ′Ω ( λ ′= 0,1,2, …) from the electronic transition. The intensity of each replica is given by the factor 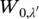 governed by Eq. (2.48); therefore, the absorption transition has the expression:
governed by Eq. (2.48); therefore, the absorption transition has the expression:
(2.51) 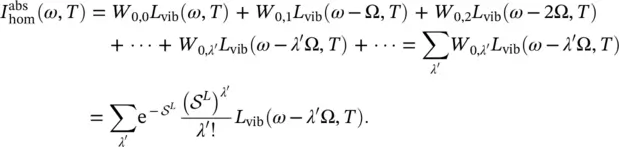
For the luminescence transition, the similarity law also applies: the overall spectrum is a series of replicas of the vibronic bands L vib( ω , T ) spaced apart by − λ Ω ( λ = 0,1,2, …) from the electronic transition:
(2.52) 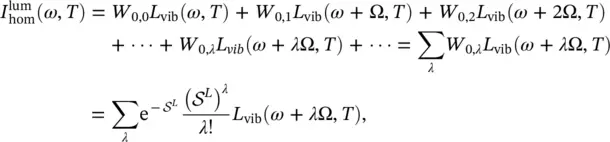
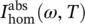 and
and 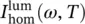 describe the spectral shape of a single defect and are therefore referred to as a homogeneous property.
describe the spectral shape of a single defect and are therefore referred to as a homogeneous property.
We note that, when the thermal excitation of the localized vibrations is taken into account ( kT ∼ ℏΩ, λ ≥0), two substantial differences emerge: the replicas L vib( ω , T ) appear in the anti‐Stokes region of the spectrum and the factor 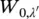 is replaced by a thermally averaged one. In this case, since the localized vibrational states with λ > 0 contribute to the spectrum, both absorption and luminescence bands widen with increasing temperature. Given a single localized mode of frequency Ω linearly coupled with the electronic transition (Huang–Rhys factor
is replaced by a thermally averaged one. In this case, since the localized vibrational states with λ > 0 contribute to the spectrum, both absorption and luminescence bands widen with increasing temperature. Given a single localized mode of frequency Ω linearly coupled with the electronic transition (Huang–Rhys factor 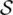 ), the width of the optical band, measured as FWHM, is given by:
), the width of the optical band, measured as FWHM, is given by:
(2.53) 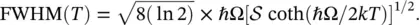
2.1.6 Inhomogeneous Effects
Till now, we have dealt with the homogeneous spectral lineshape of a single defect that is expressed by Eqs. (2.51)and (2.52)related to absorption and luminescence, respectively, which apply to the coupling with a single localized mode. In fact, the homogeneous features can be measured in systems where all defects are absolutely identical and undergo precisely identical changes under the influence of the surrounding matrix. A class of solids that quite well reproduces this condition is that of the crystals containing defects embedded exactly in equivalent positions with respect to the matrix.
A completely different framework is represented by amorphous solids where, due to the disordered network, each defect is surrounded by a different local environment; this site‐to‐site nonequivalence results in inhomogeneous effects on the spectral features [10, 11]. In the simplest approximation, it is assumed that inhomogeneous fluctuations cause an energy shift of the homogeneous spectrum as a whole without any changes in its shape, whereas the other spectroscopic parameters (transition probability, phonon energy, …) remain constant. In this case, it is convenient to introduce a one‐dimensional inhomogeneous distribution function w inh( E 00), so that w inh( E 00)Δ E represents the fraction of defects having their ZPL in the energy interval Δ E around E 00. The inhomogeneous distribution is usually described by a bell‐shaped Gaussian function:
(2.54) 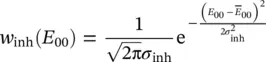
peaked at the mean energy 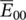 whose width σ inhdoes not depend on temperature. In the general case, the whole optical spectrum, both absorption and luminescence, is therefore given by the convolution of Eqs. ( 2.51, 2.52) and (2.54)in which the first is conveniently rewritten as a function of E 00:
whose width σ inhdoes not depend on temperature. In the general case, the whole optical spectrum, both absorption and luminescence, is therefore given by the convolution of Eqs. ( 2.51, 2.52) and (2.54)in which the first is conveniently rewritten as a function of E 00:
(2.55) 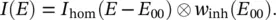
Because of the inhomogeneity effects, the vibronic spectral features are smeared out; then, the whole optical band appears to be structureless and its total width is determined by the different weights of homogeneous and inhomogeneous broadening mechanisms.
2.2 Experimental Methods and Analysis
2.2.1 Time‐Resolved Luminescence
To outline the time‐resolved experiments, we consider the interaction between the exciting light, with photon energy E excand an ensemble of noninteracting defects contained in a solid sample with thickness d , as shown in Figure 2.4. Since we are dealing with electronic transitions, we assume that, regardless of temperature, all defects are in the ground state before interacting with the excitation light and indicate their concentration as N 0.
Читать дальше

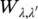 is the transition probability between the localized vibration levels in the ground and excited electronic states, and
is the transition probability between the localized vibration levels in the ground and excited electronic states, and 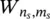 is the transition probability between the band vibration levels. In the approximation kT ≪ ℏΩ, λ = 0 and the previous equation averaged over the band vibration states is:
is the transition probability between the band vibration levels. In the approximation kT ≪ ℏΩ, λ = 0 and the previous equation averaged over the band vibration states is: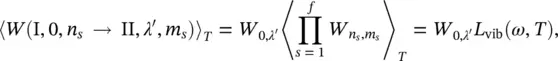
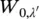 , is not influenced by the interaction with the band vibrations so that is distributed according to the Poisson distribution of Eq. (2.48). The band vibrations, in turn, give rise to an internal lineshape, L vib( ω , T ) ,featuring the properties of the vibronic band in the absence of a localized vibration: a ZPL and a vibrational background. Upon increasing temperature, the ZPL intensity decreases and the vibrational background increases so that the total intensity remains constant. L vib( ω , T ) follows a similarity law : the overall spectrum is a series of replicas of vibronic lines spaced apart by λ ′Ω ( λ ′= 0,1,2, …) from the electronic transition. The intensity of each replica is given by the factor
, is not influenced by the interaction with the band vibrations so that is distributed according to the Poisson distribution of Eq. (2.48). The band vibrations, in turn, give rise to an internal lineshape, L vib( ω , T ) ,featuring the properties of the vibronic band in the absence of a localized vibration: a ZPL and a vibrational background. Upon increasing temperature, the ZPL intensity decreases and the vibrational background increases so that the total intensity remains constant. L vib( ω , T ) follows a similarity law : the overall spectrum is a series of replicas of vibronic lines spaced apart by λ ′Ω ( λ ′= 0,1,2, …) from the electronic transition. The intensity of each replica is given by the factor 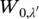 governed by Eq. (2.48); therefore, the absorption transition has the expression:
governed by Eq. (2.48); therefore, the absorption transition has the expression: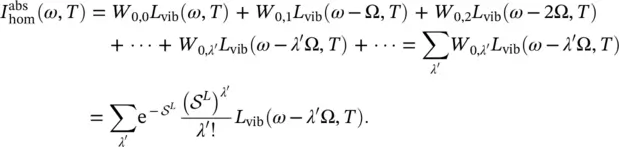
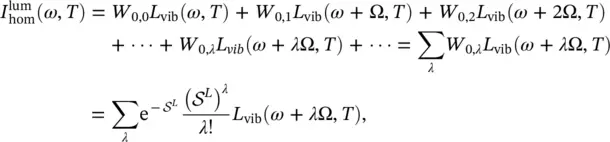
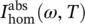 and
and 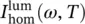 describe the spectral shape of a single defect and are therefore referred to as a homogeneous property.
describe the spectral shape of a single defect and are therefore referred to as a homogeneous property.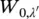 is replaced by a thermally averaged one. In this case, since the localized vibrational states with λ > 0 contribute to the spectrum, both absorption and luminescence bands widen with increasing temperature. Given a single localized mode of frequency Ω linearly coupled with the electronic transition (Huang–Rhys factor
is replaced by a thermally averaged one. In this case, since the localized vibrational states with λ > 0 contribute to the spectrum, both absorption and luminescence bands widen with increasing temperature. Given a single localized mode of frequency Ω linearly coupled with the electronic transition (Huang–Rhys factor 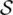 ), the width of the optical band, measured as FWHM, is given by:
), the width of the optical band, measured as FWHM, is given by: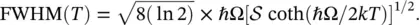
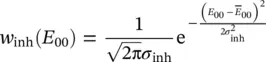
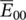 whose width σ inhdoes not depend on temperature. In the general case, the whole optical spectrum, both absorption and luminescence, is therefore given by the convolution of Eqs. ( 2.51, 2.52) and (2.54)in which the first is conveniently rewritten as a function of E 00:
whose width σ inhdoes not depend on temperature. In the general case, the whole optical spectrum, both absorption and luminescence, is therefore given by the convolution of Eqs. ( 2.51, 2.52) and (2.54)in which the first is conveniently rewritten as a function of E 00: