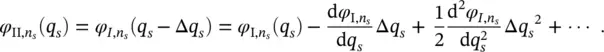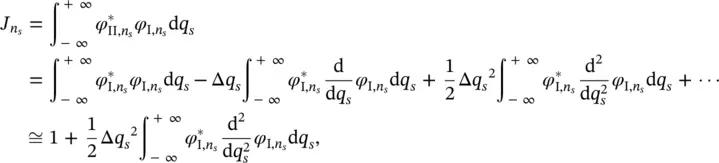The first factor is the electronic part and is proportional to the overall intensity of the absorption band. The second factor, called Franck–Condon integral , is the nuclear part; it measures the overlap between the vibrational functions of the ground and excited state and determines the band shape [10, 11].
After absorption, the nuclei relax toward the minimum energy configuration in a much shorter time (10 −12–10 −11s) than the luminescence lifetime (≥10 −9s). This implies that at the time when light emission occurs, the vibrational levels of the electronic excited state are populated in accordance with a thermal distribution. The rate of light emission is given by the relationship between the Einstein coefficients of stimulated absorption ( b ) and spontaneous emission ( a ):
(2.14) 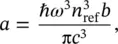
where n refis the refraction index of the medium. The emission transition probability is obtained by combining Eqs. (2.13)and (2.14). The indexes of the nuclear functions are different from those of Eq. (2.13)as a consequence of the displacement of the equilibrium position:
(2.15) 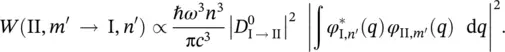
A case of particular interest is that in which the vibration frequency does not change during the electronic transition (ℏ ω I, s= ℏ ω II, s), and, consequently, W I, s( q s) and W II, s( q s) have the same curvature; this is referred to as linear electron–phonon coupling . Consequently, the vibrational wave functions in the ground and excited electronic states are equal in pairs, thus leading to a symmetrical relationship:
(2.16) 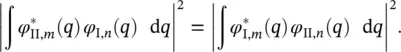
Since the absorption and luminescence transitions occur under temperature equilibrium, the vibrational n th level, both in the ground and in the excited states, are populated following the same distribution. Therefore, the symmetry property of the Franck–Condon integral ( Eq. 2.16) applies to the absorption and luminescence lineshapes; as a consequence they are characterized by a mirror symmetry with symmetry plane at the energy of the transition between the lowest vibrational levels.
Optical transitions in which the vibrational state of the system does not change are called purely electronic transitions or zero‐phonon transitions , since they occur without creation or annihilation of phonons; in this case, absorption and luminescence are resonant [6]. An example of purely electronic absorption is shown in the configuration coordinate ( q s) diagram of Figure 2.2: E 00, E 11, and E 22represent the energies of the 0 → 0, 1 → 1, and 2 → 2 transitions. In general, W I, s( q s) and W II, s( q s) have different curvatures (ℏ ω I, s≠ ℏ ω II, s), then the purely electronic transitions do not occur at the same energy and are different from ε 0: E 00≠ E 11≠ E 22≠ ε 0. In the linear electron–phonon coupling approximation (ℏ ω I, s= ℏ ω II, s), all the zero‐phonon transitions have the same energy ( E 00= E 11= E nn) coinciding with ε 0. In this case, the spectrum evidences a single line called Zero‐Phonon Line (ZPL) of energy E 00= ℏ ω 0, which is due to the superposition of a set of lines arising from transitions between different pairs of vibrational levels. Therefore, ZPL lies exactly at the energy of the purely electronic transition and is independent of temperature.
Ideally, ZPL has zero width and its shape is accounted for by the δ ‐function:
(2.17) 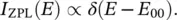
In reality, ZPL has a finite width due to the lifetime τ of the excited electronic state; δ ‐function in Eq. (2.17)is, therefore, replaced by a Lorentzian curve with full width at half maximum (FWHM) of (ℏ/ τ ):
(2.18) 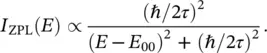
The zero‐phonon transition probability for each configuration coordinate q sis:
(2.19) 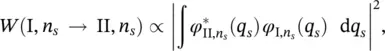
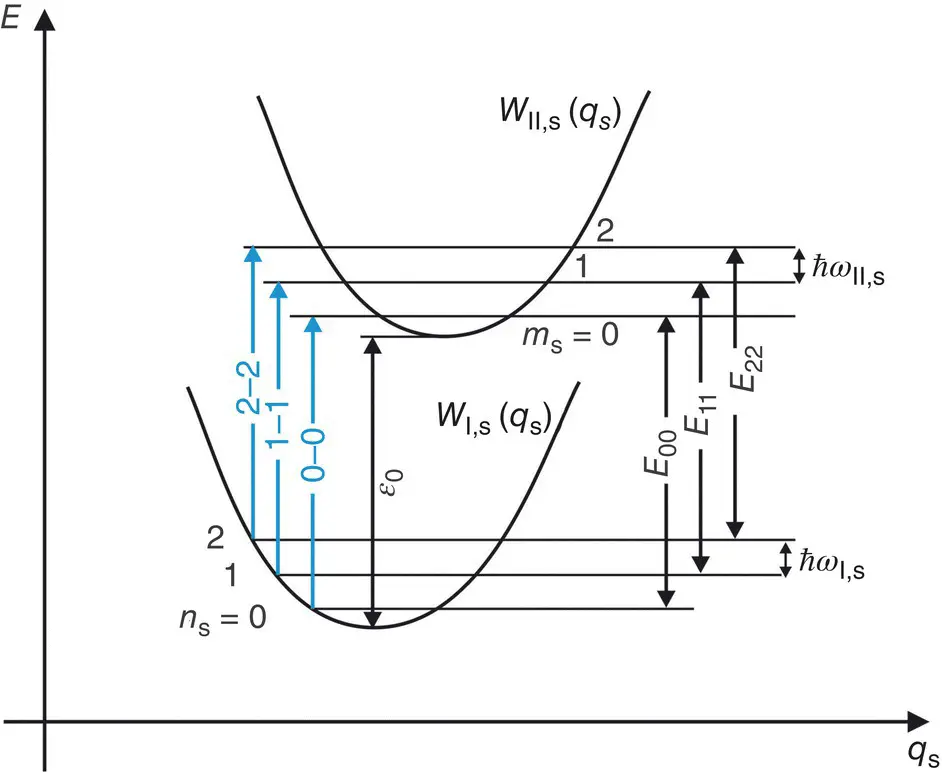
Figure 2.2Configuration coordinate diagram where are depicted the zero‐phonon transitions 0 → 0, 1 → 1, and 2 → 2.
where the vibrational levels of the electronic states I and II coincide ( n s= m s). According to Eq. (2.9), the total probability is given by:
(2.20) 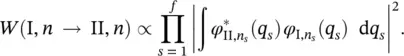
To calculate the temperature dependence of the ZPL intensity, I ZPL( T ), we have to average over the Boltzmann distribution to account for the thermal population of the vibrational levels n s:
(2.21) 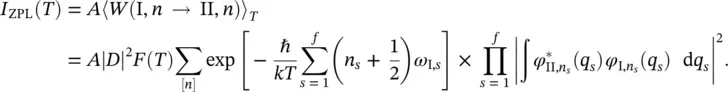
A is a constant independent of the frequency, 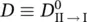 is the electron matrix element in the Condon approximation, F ( T ) is the normalizing factor of the Boltzmann's distribution function, k is the Boltzmann's constant ( k ≅1.381 × 10 −23J⋅K −1), ω I, sis the frequency of the s th normal mode in the electronic state I ,and [ n ] represents all the possible sets n s.
is the electron matrix element in the Condon approximation, F ( T ) is the normalizing factor of the Boltzmann's distribution function, k is the Boltzmann's constant ( k ≅1.381 × 10 −23J⋅K −1), ω I, sis the frequency of the s th normal mode in the electronic state I ,and [ n ] represents all the possible sets n s.
First, only the contribution of the band vibrations is considered. As discussed above, the equilibrium positions of the electronic states I and II in the configuration coordinate q sdiffer for an infinitesimal quantity Δ q s, whereas the oscillator frequencies do not change, ( ω I, s= ω II, s= ω s). The relationship between the vibrational wave functions is therefore:
(2.22) 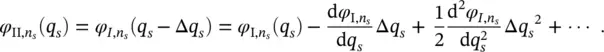
The overlap integral in Eq. (2.21)becomes:
(2.23) 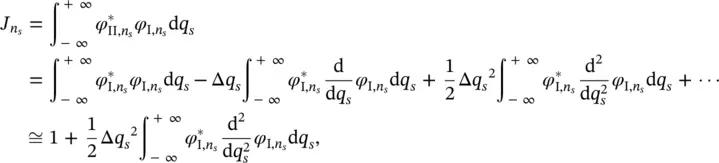
Читать дальше

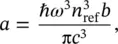
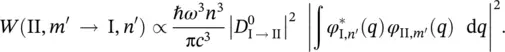
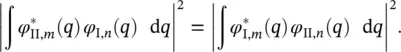
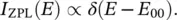
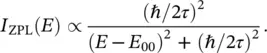
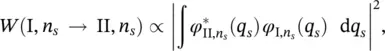

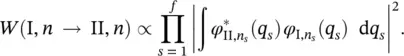
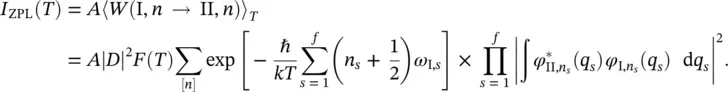
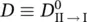 is the electron matrix element in the Condon approximation, F ( T ) is the normalizing factor of the Boltzmann's distribution function, k is the Boltzmann's constant ( k ≅1.381 × 10 −23J⋅K −1), ω I, sis the frequency of the s th normal mode in the electronic state I ,and [ n ] represents all the possible sets n s.
is the electron matrix element in the Condon approximation, F ( T ) is the normalizing factor of the Boltzmann's distribution function, k is the Boltzmann's constant ( k ≅1.381 × 10 −23J⋅K −1), ω I, sis the frequency of the s th normal mode in the electronic state I ,and [ n ] represents all the possible sets n s.