where we have account for the properties of orthonormality and symmetry of the vibrational functions. The remaining integral can be expressed in terms of the average kinetic energy:
(2.24) 
where  is the kinetic energy averaged over the n th state of the s th oscillator and M sis the nuclear mass defined in the normal mode s . According to the virial theorem:
is the kinetic energy averaged over the n th state of the s th oscillator and M sis the nuclear mass defined in the normal mode s . According to the virial theorem:
(2.25) 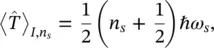
the overlap integral is:
(2.26) 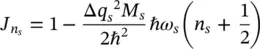
and its square is
(2.27) 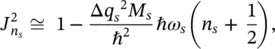
where the terms of the order of 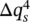 are neglected.
are neglected.
To solve Eq. (2.21), because of the independence of normal modes, the states of the oscillator 1 are separated from the remaining set n and are averaged over them:
(2.28) 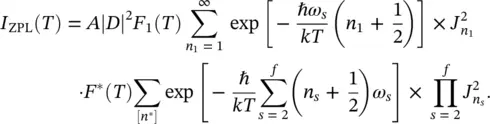
The asterisks on the indices n and on the normalizing factor F(T) mean that the oscillator 1 is excluded from the set. The first factor in Eq. (2.28)becomes:
(2.29) 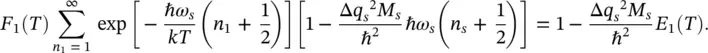
E 1( T ) is the average thermal energy of a linear harmonic oscillator:
(2.30) 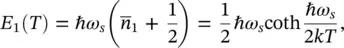
where 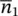 is the average quantum number of the oscillator 1. The same algorithm is applied on the states of other oscillator numbers and after a bit of algebra, the integrated intensity of ZPL is found to be:
is the average quantum number of the oscillator 1. The same algorithm is applied on the states of other oscillator numbers and after a bit of algebra, the integrated intensity of ZPL is found to be:
(2.31) 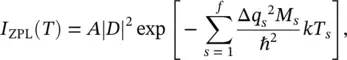
where T sis the effective temperature of a harmonic oscillator:
(2.32) 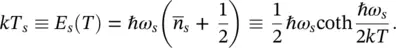
It is useful to introduce the dimensionless parameter, called Huang Rhys factor [12], for the band vibrations:
(2.33) 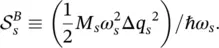
The physical meaning of the Huang Rhys factor has been introduced in the previous chapter. According to Eq. (2.33), 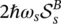 equals the difference between the absorption energy E A(vertical distance from the minimum of W I, s( q s) to W II, s( q s)) and the luminescence energy E L(vertical distance from the minimum of W II, s( q s) to W I, s( q s)). The difference between E Aand E Lis the so‐called Stokes shift ,
equals the difference between the absorption energy E A(vertical distance from the minimum of W I, s( q s) to W II, s( q s)) and the luminescence energy E L(vertical distance from the minimum of W II, s( q s) to W I, s( q s)). The difference between E Aand E Lis the so‐called Stokes shift , 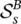 is therefore:
is therefore:
(2.34) 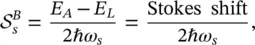
it gives the amount of the vibrational relaxation energy in units of the vibrational quantum.
After introducing 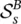 , the expression for I ZPL( T ) can be rewritten as:
, the expression for I ZPL( T ) can be rewritten as:
(2.35) 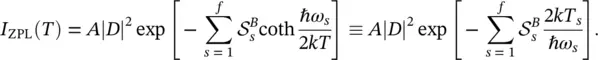
At low temperature, namely kT ≪ ℏ ω s, coth(ℏ ω s/2 kT ) → 1 or T s→ (ℏ ω s)/2 k and I ZPL( T ) becomes:
(2.36) 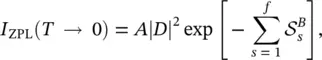
that increases with decreasing the total Huang Rhys factor , 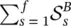 . At high temperature, namely kT ≫ ℏ ω s, coth(ℏ ω s/2 kT ) → 2 kT /ℏ ω sor kT s→ kT and the expression for I ZPL( T ) becomes:
. At high temperature, namely kT ≫ ℏ ω s, coth(ℏ ω s/2 kT ) → 2 kT /ℏ ω sor kT s→ kT and the expression for I ZPL( T ) becomes:
(2.37) 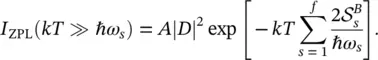
In this case, I ZPL( T ) decreases exponentially with increasing temperature and drops faster the larger is the Huang Rhys factor .
2.1.4 Phonon Line Structure
In the following, we deal with the phonon coupled transitions to succeed in describing the shape of the whole band and its temperature dependence; the effects of band vibrations and localized vibrations will be separately discussed.
As introduced in Section 2.1.1, band vibrations correspond to the transitions in which phonons of the matrix are created or annihilated. They appear as broad continuous bands whose shape, L vib( ω , T ), depends on the spectral density of phonons and on the perturbation nearby the defect. As a consequence, L vib( ω , T ) cannot be derived exactly and we will limit ourselves to indicate it by its formal expression. In fact, the integrated intensity of the whole vibronic band is given by:
(2.38) 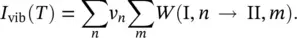
The sum over n is an average over the vibrational levels in the ground electronic state, each level having a weight v n. The sum over m corresponds to all the possible transitions from the ground to the excited state including the ZPL ( n = m ). Under the Condon approximation, the previous equation can be written as:
Читать дальше

 is the kinetic energy averaged over the n th state of the s th oscillator and M sis the nuclear mass defined in the normal mode s . According to the virial theorem:
is the kinetic energy averaged over the n th state of the s th oscillator and M sis the nuclear mass defined in the normal mode s . According to the virial theorem:
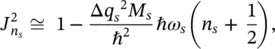
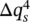 are neglected.
are neglected.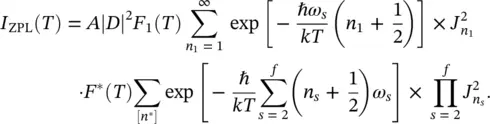
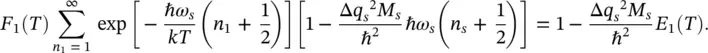
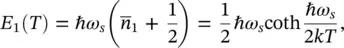
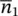 is the average quantum number of the oscillator 1. The same algorithm is applied on the states of other oscillator numbers and after a bit of algebra, the integrated intensity of ZPL is found to be:
is the average quantum number of the oscillator 1. The same algorithm is applied on the states of other oscillator numbers and after a bit of algebra, the integrated intensity of ZPL is found to be: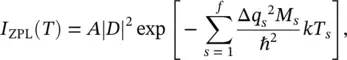
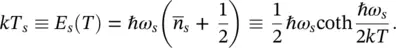
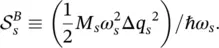
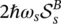 equals the difference between the absorption energy E A(vertical distance from the minimum of W I, s( q s) to W II, s( q s)) and the luminescence energy E L(vertical distance from the minimum of W II, s( q s) to W I, s( q s)). The difference between E Aand E Lis the so‐called Stokes shift ,
equals the difference between the absorption energy E A(vertical distance from the minimum of W I, s( q s) to W II, s( q s)) and the luminescence energy E L(vertical distance from the minimum of W II, s( q s) to W I, s( q s)). The difference between E Aand E Lis the so‐called Stokes shift , 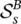 is therefore:
is therefore: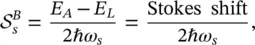
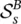 , the expression for I ZPL( T ) can be rewritten as:
, the expression for I ZPL( T ) can be rewritten as: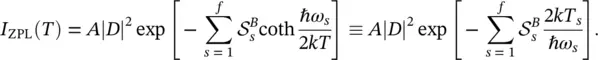
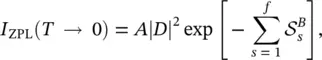
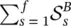 . At high temperature, namely kT ≫ ℏ ω s, coth(ℏ ω s/2 kT ) → 2 kT /ℏ ω sor kT s→ kT and the expression for I ZPL( T ) becomes:
. At high temperature, namely kT ≫ ℏ ω s, coth(ℏ ω s/2 kT ) → 2 kT /ℏ ω sor kT s→ kT and the expression for I ZPL( T ) becomes: