Aiden A. Bruen - Cryptography, Information Theory, and Error-Correction
Здесь есть возможность читать онлайн «Aiden A. Bruen - Cryptography, Information Theory, and Error-Correction» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Cryptography, Information Theory, and Error-Correction
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Cryptography, Information Theory, and Error-Correction: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Cryptography, Information Theory, and Error-Correction»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
A rich examination of the technologies supporting secure digital information transfers from respected leaders in the field Cryptography, Information Theory, and Error-Correction: A Handbook for the 21ST Century
Cryptography, Information Theory, and Error-Correction

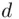 between 1 and 39 such that
between 1 and 39 such that 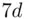 gives a remainder of 1 when divided by 40. In this case, it turns out that
gives a remainder of 1 when divided by 40. In this case, it turns out that 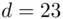 (more on this later) since
(more on this later) since 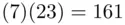 and 161 leaves a remainder of 1 on division by 40. Here, 40 comes from the fact that
and 161 leaves a remainder of 1 on division by 40. Here, 40 comes from the fact that 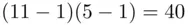 and 5, 11 are the factors of
and 5, 11 are the factors of 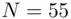 .
.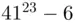 is divisible by 55.
is divisible by 55. – or in general any
– or in general any 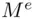 – on a calculator or a computer, we run into overflow problems. To avoid them, we use this principle, combined with the repeated squaring method. Here is how this method works in the present case. We first express 23 as a sum of powers of 2. Thus,
– on a calculator or a computer, we run into overflow problems. To avoid them, we use this principle, combined with the repeated squaring method. Here is how this method works in the present case. We first express 23 as a sum of powers of 2. Thus, 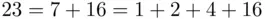 . So if
. So if 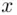 is any number, we have
is any number, we have 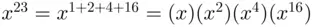 . Each number in this product is the square of the previous number except for
. Each number in this product is the square of the previous number except for 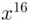 which is the square of the square of the previous number.
which is the square of the square of the previous number.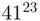 and get the remainder upon division by 55.
and get the remainder upon division by 55.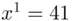 , nothing more to do. Then,
, nothing more to do. Then, 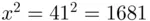 gives a remainder of 31 when divided by 55. Proceeding, instead of calculating
gives a remainder of 31 when divided by 55. Proceeding, instead of calculating 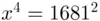 by squaring
by squaring 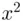 , we need only calculate
, we need only calculate 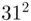 and get the remainder on division by 55 which is 26. Now, to get the next term in the product (namely
and get the remainder on division by 55 which is 26. Now, to get the next term in the product (namely 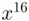 ) instead of squaring
) instead of squaring 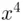 – to get
– to get 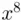 – and then squaring again to get
– and then squaring again to get 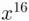 – we need only square 26, get the remainder and square the remainder again and finally get the remainder on division by 55 which is 36. So the four remainders for
– we need only square 26, get the remainder and square the remainder again and finally get the remainder on division by 55 which is 36. So the four remainders for 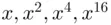 are 41, 31, 26, 36. In principle, now we have to multiply 41 by 31 by 26 by 36 and get the remainder on division by 55. Again, we can take shortcuts using Principle 2. We can multiply 41 by 31 and get the remainder. We calculate
are 41, 31, 26, 36. In principle, now we have to multiply 41 by 31 by 26 by 36 and get the remainder on division by 55. Again, we can take shortcuts using Principle 2. We can multiply 41 by 31 and get the remainder. We calculate 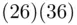 and get the remainder (on division by 55). Multiplying the 2 remainders together, and getting the remainder, on division by 55, gives us the answer. The two remainders are 6 and 1. Then
and get the remainder (on division by 55). Multiplying the 2 remainders together, and getting the remainder, on division by 55, gives us the answer. The two remainders are 6 and 1. Then 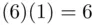 and B ends up recovering the message which is 6. Note that in the example above,
and B ends up recovering the message which is 6. Note that in the example above, 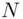 is the product
is the product 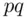 of two distinct primes
of two distinct primes 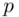 and
and 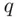 with
with 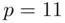 and
and 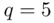 . The enciphering index
. The enciphering index 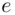 is 7 , M is 6, the cipher text
is 7 , M is 6, the cipher text 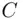 is 41, and the deciphering index
is 41, and the deciphering index 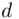 is 23.
is 23.










