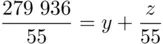Using encryption for storing messages and files is another important function of encryption in today's society. As an example, we mention the encryption of a file – or even an entire hard drive (or solid state drive) – in a computer so that, if it is set aside (or stolen) an individual other than the owner cannot access the contents. (Apple and Windows both have encryption applications that use XTS‐AES‐128 encryption with a 256‐bit key. Apple's MacOS uses it in FileVault 2, [App18], and Windows 10 version 1511 uses it in their Bitlocker feature, [Win19].) We can fit this into our previous general situation with the owner of the computer playing the role of both Aand B.
We have been silent on how Aand Bget their enciphering and deciphering keys. This is discussed in a later chapter, but will depend on the kind of encryption being used. The two fundamentally different possibilities for cryptography are as follows:
1 Symmetric Cryptography
2 Asymmetric Cryptography, i.e. Public Key Cryptography.
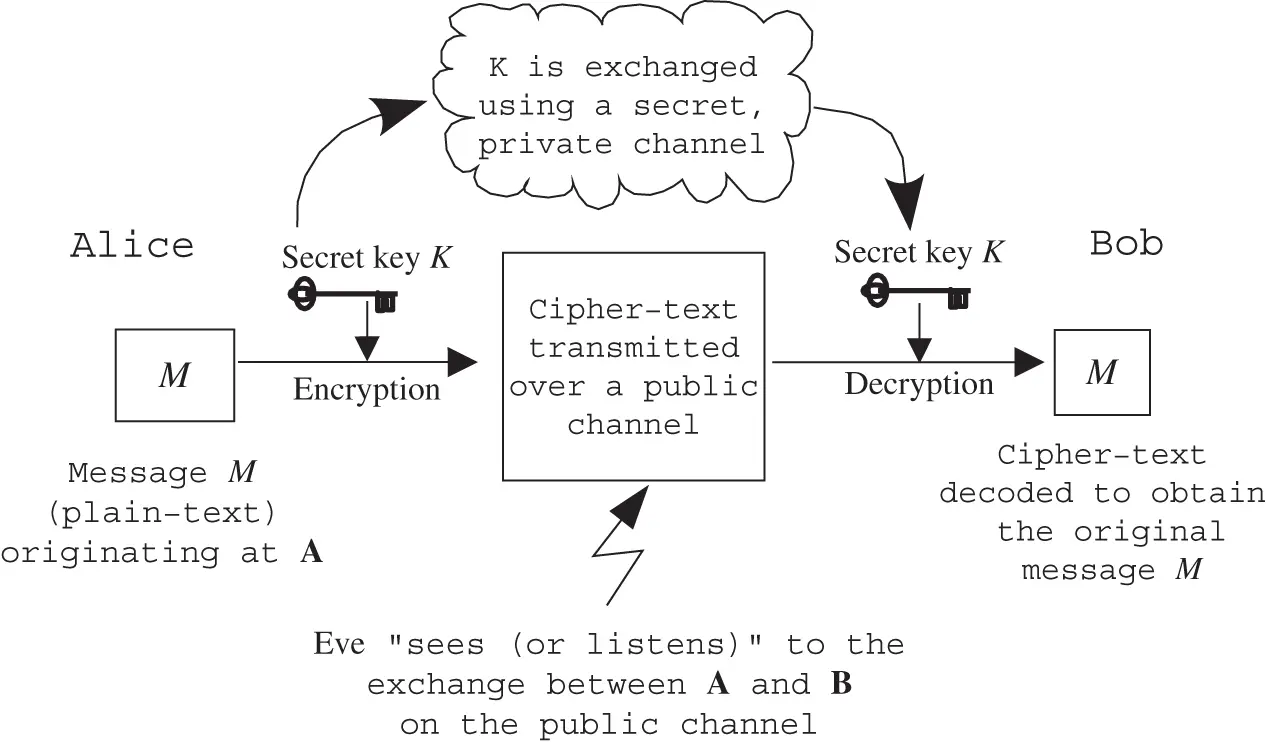
Figure 3.2Symmetric encryption.
Recall that as before A, Bare the communicating entities and Awants to send a secret message  to B( Figure 3.2). In symmetric encryption, there are three features.
to B( Figure 3.2). In symmetric encryption, there are three features.
1 The enciphering key used by the transmitter A is equal to the deciphering key used by the receiver B and this key is known only to A and B.
2 The enciphering algorithm, converting the plain text to cipher text, is such that the cipher text can be calculated immediately given and .
3 The deciphering algorithm, converting back to , can be calculated immediately given and .
The security depends on the fact that the secret key  is known only to Aand B.
is known only to Aand B.
Public key cryptography works differently ( Figure 3.3). The procedure is as follows:
1 The enciphering key used by A (or anybody else) to send a message to B is publicly known, and is called the public key of B. However, the deciphering key used by B to decrypt the cipher text is known only to B and is the private key of B. So the two keys are quite different.
2 The enciphering procedure, converting the plain text to cipher text , can be immediately calculated given M and .
3 The deciphering procedure, converting back to M, can be calculated immediately by B using . However, it is not possible for somebody else who is not in possession of to convert back to M in a reasonable amount of time.The security of public key cryptography rests on the assumption that it is not feasible to convert back to M without knowledge of the private key .Thus, in public key cryptography each user B in a network has a public key and a private key , which are supplied by a public key authority (PKA).
Symmetric cryptography (encryption) is also called secret key cryptography (encryption). The security depends, as stated above, on the assumption that only the communicating parties Aand Bknow the (common) key. Note that A, Bcould also denote groups of entities on a network and that Bcan also send a secret message to Ausing their common secret key.
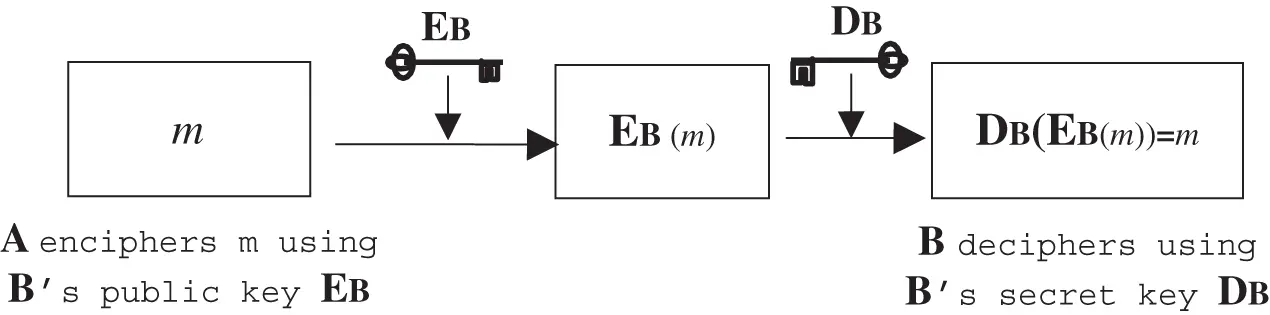
Figure 3.3Asymmetric or public encryption.
Historically, cryptography meant symmetric cryptography. Nowadays, important symmetric algorithms in use are AESand the One‐Time Padwhich is sometimes derived from a shift register (see Chapter 16).
3.2 Public Key Cryptography and RSA on a Calculator
We now turn to some examples of asymmetric or public key cryptography. First, let us explain RSA, the main public key algorithm. As before, Awants to send a secret message  to B. For convenience, let us think of
to B. For convenience, let us think of  as being the number 6, say, as in our previous example. We make the encryption more complicated. So instead of saying “add 7,” we say “multiply 6 by itself 7 times” i.e. calculate
as being the number 6, say, as in our previous example. We make the encryption more complicated. So instead of saying “add 7,” we say “multiply 6 by itself 7 times” i.e. calculate  . As an extra complication, let us take some number
. As an extra complication, let us take some number  and declare the encryption algorithm to be “multiply 6 by itself 7 times and take the remainder of this number when divided by
and declare the encryption algorithm to be “multiply 6 by itself 7 times and take the remainder of this number when divided by 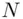 to be the cipher text
to be the cipher text 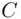 .” As a small working example, let
.” As a small working example, let 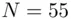 . So our cipher text is the remainder of
. So our cipher text is the remainder of 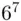 upon division by 55. This remainder is easily calculated, using any calculator, as follows:
upon division by 55. This remainder is easily calculated, using any calculator, as follows:
We want to find the (unique) remainder 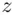 that is left over when we divide 279 936 by 55. So we have
that is left over when we divide 279 936 by 55. So we have
(3.5) 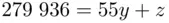
where 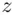 is one of
is one of 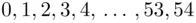 . We are not really interested in the value of
. We are not really interested in the value of 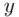 : we just need
: we just need 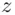 . Dividing across by 55 in Eq. (3.5), we get
. Dividing across by 55 in Eq. (3.5), we get
(3.6) 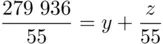
Читать дальше


 to B( Figure 3.2). In symmetric encryption, there are three features.
to B( Figure 3.2). In symmetric encryption, there are three features.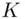 is known only to Aand B.
is known only to Aand B.
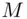 to B. For convenience, let us think of
to B. For convenience, let us think of 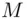 as being the number 6, say, as in our previous example. We make the encryption more complicated. So instead of saying “add 7,” we say “multiply 6 by itself 7 times” i.e. calculate
as being the number 6, say, as in our previous example. We make the encryption more complicated. So instead of saying “add 7,” we say “multiply 6 by itself 7 times” i.e. calculate  . As an extra complication, let us take some number
. As an extra complication, let us take some number 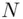 and declare the encryption algorithm to be “multiply 6 by itself 7 times and take the remainder of this number when divided by
and declare the encryption algorithm to be “multiply 6 by itself 7 times and take the remainder of this number when divided by 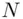 to be the cipher text
to be the cipher text 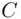 .” As a small working example, let
.” As a small working example, let 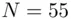 . So our cipher text is the remainder of
. So our cipher text is the remainder of 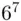 upon division by 55. This remainder is easily calculated, using any calculator, as follows:
upon division by 55. This remainder is easily calculated, using any calculator, as follows: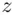 that is left over when we divide 279 936 by 55. So we have
that is left over when we divide 279 936 by 55. So we have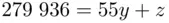
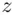 is one of
is one of 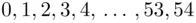 . We are not really interested in the value of
. We are not really interested in the value of 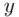 : we just need
: we just need 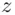 . Dividing across by 55 in Eq. (3.5), we get
. Dividing across by 55 in Eq. (3.5), we get