Aiden A. Bruen - Cryptography, Information Theory, and Error-Correction
Здесь есть возможность читать онлайн «Aiden A. Bruen - Cryptography, Information Theory, and Error-Correction» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Cryptography, Information Theory, and Error-Correction
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:5 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Cryptography, Information Theory, and Error-Correction: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Cryptography, Information Theory, and Error-Correction»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
A rich examination of the technologies supporting secure digital information transfers from respected leaders in the field Cryptography, Information Theory, and Error-Correction: A Handbook for the 21ST Century
Cryptography, Information Theory, and Error-Correction

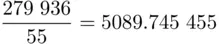
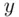 is
is 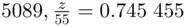 so
so 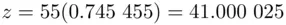 . This is not what we were hoping for :
. This is not what we were hoping for : 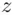 is supposed to be a whole number, namely the remainder when 279936 is divided by 55! However, the calculator has made rounding errors, and we suspect that
is supposed to be a whole number, namely the remainder when 279936 is divided by 55! However, the calculator has made rounding errors, and we suspect that 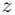 is 41 (and
is 41 (and 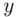 is 5089). This is easily checked. We can verify that Eq. ( 3.5) checks out with
is 5089). This is easily checked. We can verify that Eq. ( 3.5) checks out with 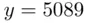 ,
,  since
since 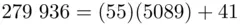 .
.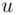 by another positive integer
by another positive integer 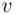 .
.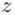 is unique? Maybe there are two possible values?
is unique? Maybe there are two possible values?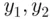 being positive and
being positive and 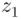 and
and 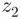 both lying between 0 and 54. So we have
both lying between 0 and 54. So we have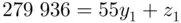
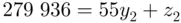
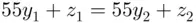 . Now, if
. Now, if 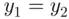 it follows that
it follows that 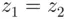 . So assume that
. So assume that 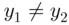 . Call the larger one
. Call the larger one 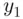 , so
, so 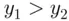 .
.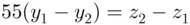 . Since
. Since 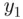 is at least 1 bigger than
is at least 1 bigger than 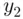 , we get that the left side is at least 55. Since
, we get that the left side is at least 55. Since 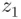 and
and 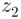 are between 0 and 54, we see that the right side is at most 54. Since
are between 0 and 54, we see that the right side is at most 54. Since 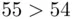 , we conclude that the assumption
, we conclude that the assumption 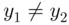 leads to a contradiction. Thus,
leads to a contradiction. Thus, 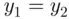 (and so also
(and so also 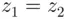 ): end of story. As a consequence, to check Eq. ( 3.5 ) in the future all we need to do in the case above is to ensure that
): end of story. As a consequence, to check Eq. ( 3.5 ) in the future all we need to do in the case above is to ensure that 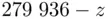 is divisible by 55.
is divisible by 55.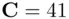 to B having calculated this from the message
to B having calculated this from the message 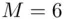 . How does B recover
. How does B recover 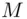 from 41? B knows that
from 41? B knows that 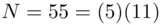 . Since we are using a public cryptosystem, the enciphering algorithm is public knowledge (in this particular example), the enciphering algorithm is “multiply the message by itself seven times and take the remainder on division by
. Since we are using a public cryptosystem, the enciphering algorithm is public knowledge (in this particular example), the enciphering algorithm is “multiply the message by itself seven times and take the remainder on division by 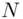 ”: this gives the cipher text 41. B calculates the deciphering index
”: this gives the cipher text 41. B calculates the deciphering index 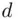 as follows.
as follows.










