What we mean by “not unique” is that there may be more than one value of 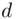 such that the remainder of
such that the remainder of 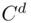 , on division by
, on division by 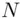 , is
, is 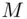 . The reason for nonuniqueness is that, instead of working with
. The reason for nonuniqueness is that, instead of working with 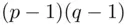 , we can work with any number
, we can work with any number 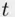 that is divisible by
that is divisible by 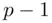 and
and  , as explained in the algorithm description and in Chapter 19. It is often possible to find
, as explained in the algorithm description and in Chapter 19. It is often possible to find 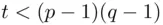 so that the calculations are simplified, and we get a shortcut even if the resulting
so that the calculations are simplified, and we get a shortcut even if the resulting 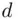 is the same.
is the same.
We present new insights on public key and symmetric encryption.
3.1 The Basic Idea of Cryptography
Cryptography is an old subject dating back at least as far as 1500 BCE. A technique developed by Porta associated also with Vigenère in the Middle Ages is close to the cutting edge of part of modern cryptography. Additionally, cryptography is closely connected to information theory and error‐correction, with many fundamental ideas going back to Claude Shannon. Further details about Shannon and the history of cryptography are provided in Chapter 1.
Cryptography is the art of keeping messages secret. Imagine that A, Bare two entities who wish to communicate in secret. Assume Awants to send a secret message to B.
The procedure is as follows ( Figure 3.1). First, Ascrambles the message using a cryptographic key . The process of scrambling the message is called encryption : alternatively, A enciphers the message.

Figure 3.1General encryption.
The encryption or enciphering scrambles the message 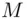 , that is, the plain text, into unintelligible output called the cipher text. Next, the sender Atransmits in the open (publicly) the cipher text
, that is, the plain text, into unintelligible output called the cipher text. Next, the sender Atransmits in the open (publicly) the cipher text 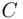 to the receiver B. When Breceives the cipher text, Bdescrambles or deciphers the cipher text using a key that may or may not be the same as the original key used by A. Bcan now recover the original message
to the receiver B. When Breceives the cipher text, Bdescrambles or deciphers the cipher text using a key that may or may not be the same as the original key used by A. Bcan now recover the original message 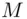 that was transmitted by A.
that was transmitted by A.
In summary, the sender Aencrypts or enciphers the message 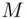 into unintelligible cipher text
into unintelligible cipher text 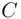 using an encrypting or enciphering key. The enciphering is done by a specific procedure involving a sequence of steps or rules called the enciphering algorithm (or encryption algorithm ).
using an encrypting or enciphering key. The enciphering is done by a specific procedure involving a sequence of steps or rules called the enciphering algorithm (or encryption algorithm ).
Using the decryption or deciphering key , and using the deciphering algorithm ( decryption algorithm ), the receiver Bthen decrypts or deciphers 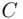 and thus recovers the original message
and thus recovers the original message 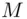 that was transmitted by the transmitter A. Moreover, at least in theory, an intruder Eve cannot access the message
that was transmitted by the transmitter A. Moreover, at least in theory, an intruder Eve cannot access the message 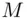 since Eve will not have the decryption key that is needed for decrypting (deciphering, inverting)
since Eve will not have the decryption key that is needed for decrypting (deciphering, inverting) 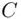 to recover
to recover 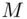 .
.
Evidently, everything depends on Bbeing the sole possessor of the decryption key, apart possibly from A. (If the decryption and encryption keys are the same – as they are in symmetric encryption, then Aalso has the decryption key).
Generally speaking, a key is a mathematical object such as a number (or several numbers) or a string of zeros and ones, i.e. a binary string such as the binary string (1 1 0 1) of length 4.
The enciphering and deciphering operations are usually mathematical procedures. For example, let us suppose that the enciphering key is the number 7 and that the enciphering operation is “add 7.” Suppose the secret message that Awants to transmit to Bis the number 6. (For example Amight be directing her stockbroker Bto buy six thousand shares of a given security on the stock market).
Then, Acalculates the cipher text 13 ( = 6 plus 7) and transmits this to B. Now, Bknows that the enciphering transformation is “add 7.” To undo, or invert this, Bsubtracts 7 from 13 (as this is the deciphering operation) and ends up recovering the original message transmitted by A, namely 6.
It should be mentioned that the cryptographic keys above need not be mathematical objects: in fact, historically, they often were not. A famous example, mentioned in Chapter 1, occurred in World War II when, in effect, the key was an entire language! This was the Navajo language used by the Navajo tribe in Arizona and adapted for encryption purposes by the US armed forces around 1942. Enciphering consisted of translating messages from English into the Navajo language, while deciphering simply meant translating Navajo back to English at the other end. At that time, this symmetric encryption was extremely effective.
Читать дальше

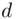 such that the remainder of
such that the remainder of 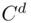 , on division by
, on division by 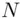 , is
, is 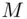 . The reason for nonuniqueness is that, instead of working with
. The reason for nonuniqueness is that, instead of working with 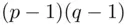 , we can work with any number
, we can work with any number 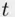 that is divisible by
that is divisible by 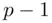 and
and  , as explained in the algorithm description and in Chapter 19. It is often possible to find
, as explained in the algorithm description and in Chapter 19. It is often possible to find 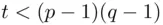 so that the calculations are simplified, and we get a shortcut even if the resulting
so that the calculations are simplified, and we get a shortcut even if the resulting 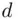 is the same.
is the same.
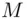 , that is, the plain text, into unintelligible output called the cipher text. Next, the sender Atransmits in the open (publicly) the cipher text
, that is, the plain text, into unintelligible output called the cipher text. Next, the sender Atransmits in the open (publicly) the cipher text 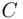 to the receiver B. When Breceives the cipher text, Bdescrambles or deciphers the cipher text using a key that may or may not be the same as the original key used by A. Bcan now recover the original message
to the receiver B. When Breceives the cipher text, Bdescrambles or deciphers the cipher text using a key that may or may not be the same as the original key used by A. Bcan now recover the original message 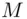 that was transmitted by A.
that was transmitted by A.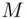 into unintelligible cipher text
into unintelligible cipher text 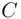 using an encrypting or enciphering key. The enciphering is done by a specific procedure involving a sequence of steps or rules called the enciphering algorithm (or encryption algorithm ).
using an encrypting or enciphering key. The enciphering is done by a specific procedure involving a sequence of steps or rules called the enciphering algorithm (or encryption algorithm ).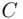 and thus recovers the original message
and thus recovers the original message 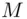 that was transmitted by the transmitter A. Moreover, at least in theory, an intruder Eve cannot access the message
that was transmitted by the transmitter A. Moreover, at least in theory, an intruder Eve cannot access the message 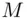 since Eve will not have the decryption key that is needed for decrypting (deciphering, inverting)
since Eve will not have the decryption key that is needed for decrypting (deciphering, inverting) 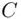 to recover
to recover 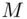 .
.










