12 2.12 The corresponding cipher text is JCJDUKJ.The initial settings are the following: = (0 15 6 10 14 8 19 17 22 18 11) (1 2 9 13 21 25) (3 4 23 5 24 7 12 16 20) = (0 7 9 4 6 18 23 25 8) (1 17 19) (2 20 10) (3 12) (5 11 13 21) (14 22 15 16 24) = (0 2 4 7 16 17 19 5) (1 6 3 8 21 24 11 13 9 10 25 12 14 15) (18 23 20 22) = (0 4)(1 7)(2 9)(3 16)(5 20)(6 8)(10 19)(11 17)(12 25)(13 18)(14 24)(15 22)(21 23) = (11 18 22 17 19 8 14 10 6 15 0) (25 21 13 9 2 1) (20 16 12 7 24 5 23 4 3) = (8 25 23 18 6 4 9 7 0) (19 17 1) (10 20 2) (12 3) (21 13 11 5) (24 16 15 22 14) = (5 19 17 16 7 4 2 0) (15 14 12 25 10 9 13 11 24 21 8 3 6 1) (22 20 23 18)Also, the initial settings were defined as follows:, , Using the given information, the cipher text was obtained as follows:1st letter: (m)Reaching the reflector, we get Now following the signal back through the rotors, we obtainTherefore, the first cipher text character is J.Now, we must update the rotor settings: .For the remaining characters, proceed through the same process. Remember, when changes from 25 back to 0, update to 8 (this occurs after the fourth cipher text character is computed).
13 2.13 After writing the cipher text on two strips of paper, we obtain the following table:Displacement# of coincidences1420334353667184Here we note that the maximum number of coincidences occurs for a displacement of 6. Therefore, the period is either 3 or 6, because the displacement producing the largest number of coincidences is a scalar multiple of the period.
14 2.14 To complete the problem, we will try a period of 3 first. If it doesn't succeed, we will try the second choice of 6. With our results, we will find the most common letter and assume it deciphers to “e.” If there are ties for the most frequent character, we will investigate each case individually to determine the most probable choice.Starting with the first letter of the keyword, we create a table of cipher text frequencies:The first, fourth, seventh, letters of cipher text areLKXRSXOZBXZDBUYFGROSWDDOOICSDXNSVESKOX.From this, we computeABCDEFGHIJKLM0214111010210NOPQRSTUVWXYZ1500250111502Here we note that the most frequent cipher text letters are O, S, and X. Now, we have to consider each letter to determine which is most likely the key letter. If O deciphers to “e”(yielding a key letter of “K”), then S i, and X n. Looking at Table 2.1, the number of occurrences of “i and “n” in the cipher text are reasonable. Alternatively, if S deciphers to “e” (yielding a key letter of “O”), then O “a” and X “j”. However, 5 occurrences out of 38 letters is far too high for j (the frequency of j is 0.002%). Finally, if X deciphers to “e,” (yielding a key letter of “T”), then O “v” and S “y.” Again, 5 occurrences for each “v” and “y” in 38 letters are far too high to be correct. Therefore, “K” is the most probable key letter.We use the same reasoning for the next two key letters. For the second, fifth, eighth, letters, we compute:ABCDEFGHIJKLM1010323282213NOPQRSTUVWXYZ0100200110410Here we have an overwhelming choice for “e,” namely “I.” Thus, if I deciphers to “e,” we have a key letter of “E.”Similarly, for the third, sixth, nineth, letters, we computeABCDEFGHIJKLM3150024012022NOPQRSTUVWXYZ0051421000011This gives us two likely choices for “e,” although two others are very close. If “C' deciphers to “e,” we have a key letter of “Y.” If this is the case, them G “I,” R “t,” and P “r,” all of which have a reasonable number of occurrences. If, on the other hand, P deciphers to “e,” then the key letter is “L.” This would mean that C “r,” G “v,” and R “g.” However, the number of occurrences of both “v” and “g” are too high to be realistic. Therefore, we arrive at a key letter of “Y,” producing a keyword of “key.”To make sure that 3 is the period, one can use the newly acquired keyword to decipher the message. For long messages, it is nearly impossible that two separate messages would appear out of the same piece of cipher text. Thus, if the first key works, we are done. If not, then the period is likely 6 instead. This problem illustrates the ambiguities one can run into when attempting to break the Vigenère cipher, and serves as a reminder to use the methods outlined here with diligence and care.
15 2.15 Repeat the exact same process as in Problem 2.14, inputting the letters YDDMYU with the same initial settings as before. The resulting output is the message “attack.”
16 2.16 If the book contained typical English text, then the frequencies should be very similar to the table.
Chapter 3 RSA, Key Searches, TLS, and Encrypting Email
Goals, DiscussionThis chapter is important and does not require too much mathematical background. We avoid making essential use of number theory in the text, although it can be used to shorten the calculations. We discuss one of the main public key algorithms, namely RSA, as well as some of its applications to e‐Commerce with Transport Layer Security (TLS) and to the encryption of email.
Public key and symmetric cryptography are discussed as well as the average number of guesses required when searching a key space for the key ( Theorem 3.6). Some cryptographic attacks, both mathematical and real world are discussed here and in Chapter 7.
In Section 3.7, we discuss another important algorithm which straddles the border between symmetric and public‐key exchanges, called the Diffie–Hellman key‐exchange.
In Section 3.3, we denote by 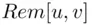 the remainder
the remainder 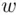 when the positive integer
when the positive integer 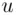 is divided by the positive integer
is divided by the positive integer 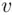 . For example,
. For example, 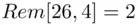 . Another way of stating this is that
. Another way of stating this is that 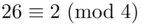 or
or 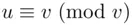 . We are working here with the integers
. We are working here with the integers 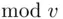 . This is covered in detail in Chapters 5and 19.
. This is covered in detail in Chapters 5and 19.
Let us briefly explain the idea. Alice wants to send a secret message to Bob. Bob has chosen a number 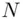 and another number
and another number 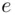 (for encryption). The pair
(for encryption). The pair 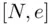 represents Bob's public key and is listed in a “public key directory.” Alice represents the secret message as a number
represents Bob's public key and is listed in a “public key directory.” Alice represents the secret message as a number 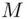 lying between 1 and
lying between 1 and 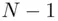 . To encrypt or scramble the message
. To encrypt or scramble the message 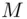 , Alice multiplies
, Alice multiplies 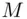 by itself
by itself 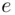 times, gets the remainder after dividing by
times, gets the remainder after dividing by 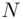 , and transmits the result to Bob. The result is called the cipher text
, and transmits the result to Bob. The result is called the cipher text 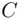 . An eavesdropper, noting
. An eavesdropper, noting 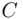 , realizes the message itself must be equal to the
, realizes the message itself must be equal to the 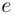 th root of
th root of 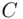 , or
, or 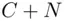 , or
, or 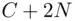 , or
, or 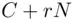 for some unknown
for some unknown 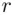 . Eve (the eavesdropper) cannot find
. Eve (the eavesdropper) cannot find 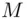 as there are too many values of
as there are too many values of 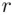 to try. It is a remarkable fact that if there is just a single value of
to try. It is a remarkable fact that if there is just a single value of 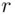 , say
, say 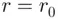 , such that the
, such that the 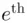 root of
root of 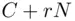 is a whole number lying between 1 and
is a whole number lying between 1 and 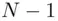 . To see this, let
. To see this, let 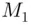 be any whole number, i.e. a positive integer not necessarily lying between 1 and
be any whole number, i.e. a positive integer not necessarily lying between 1 and 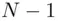 such that
such that 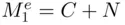 . Then
. Then
Читать дальше

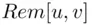 the remainder
the remainder 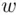 when the positive integer
when the positive integer 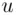 is divided by the positive integer
is divided by the positive integer 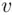 . For example,
. For example, 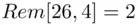 . Another way of stating this is that
. Another way of stating this is that 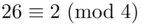 or
or 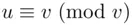 . We are working here with the integers
. We are working here with the integers 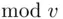 . This is covered in detail in Chapters 5and 19.
. This is covered in detail in Chapters 5and 19.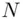 and another number
and another number 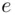 (for encryption). The pair
(for encryption). The pair 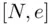 represents Bob's public key and is listed in a “public key directory.” Alice represents the secret message as a number
represents Bob's public key and is listed in a “public key directory.” Alice represents the secret message as a number 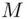 lying between 1 and
lying between 1 and 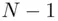 . To encrypt or scramble the message
. To encrypt or scramble the message 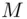 , Alice multiplies
, Alice multiplies 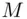 by itself
by itself 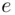 times, gets the remainder after dividing by
times, gets the remainder after dividing by 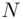 , and transmits the result to Bob. The result is called the cipher text
, and transmits the result to Bob. The result is called the cipher text 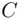 . An eavesdropper, noting
. An eavesdropper, noting 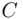 , realizes the message itself must be equal to the
, realizes the message itself must be equal to the 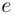 th root of
th root of 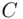 , or
, or 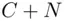 , or
, or 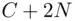 , or
, or 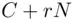 for some unknown
for some unknown 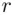 . Eve (the eavesdropper) cannot find
. Eve (the eavesdropper) cannot find 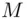 as there are too many values of
as there are too many values of 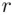 to try. It is a remarkable fact that if there is just a single value of
to try. It is a remarkable fact that if there is just a single value of 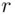 , say
, say 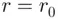 , such that the
, such that the 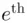 root of
root of 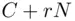 is a whole number lying between 1 and
is a whole number lying between 1 and 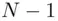 . To see this, let
. To see this, let 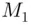 be any whole number, i.e. a positive integer not necessarily lying between 1 and
be any whole number, i.e. a positive integer not necessarily lying between 1 and 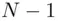 such that
such that 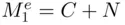 . Then
. Then










