Aiden A. Bruen - Cryptography, Information Theory, and Error-Correction

(3.1)

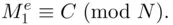
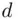Let be a decryption index (there may be several). If 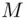is the message, then, by definition,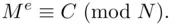

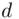(3.2)

Applying , we have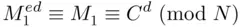

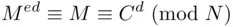
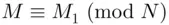(3.3)

and

(3.4)

Therefore, . In particular, if 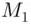lies between 1 and 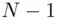, as does 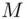by assumption, then 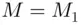. In effect, we are saying that the mapping 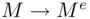is 1 to 1 if 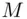lies between 1 and .

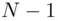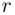Moreover, it can be shown that if for any positive integer the 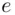th root of 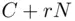is a whole number , then the remainder of 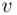upon division by 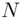must be 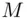(see Chapter 19).

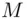The recipient Bob, however, can calculate immediately from a formula involving his private key consisting of a “decryption index” 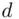along with two prime numbers 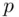, 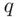. The reason is that 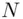is the product of and 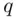. Bob knows 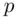and 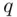. Anybody else, even knowing 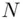, cannot in general determine what the factors 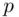, 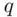are in a reasonable amount of time.

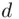Eve can try guessing the message without knowing by guessing 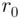. Alternatively, Eve can try guessing 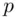and 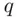from which she can calculate 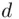. In other words, Eve can try to guess the private key and then determine the message.

We detail some potential weaknesses with public key algorithms such as RSA. However, this algorithm is still a central public key algorithm. Its security, when carefully implemented, seems to still be strong after many years of constant use.

A fact in cryptography is that in a brute‐force attackon a key‐space (one where we try all possible keys), the correct key is likely to be found after trying about half the total number of keys. In this chapter, we provide a short simple proof of this fact.

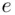The encryption exponent mentioned above must be chosen to have no factors in common with 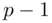and no factors in common with . The reason for assuming this is so that 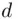exists. Another reason is that this condition must be satisfied in order that two different messages get two different encryptions. This comes up in Problem 3.1. We mention also that, for a given 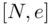, the decryption index need not be unique!We provide several examples. This is important because some attacks on RSA are possible if 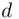is small; we refer to Chapter 7. So if 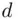is not unique, this makes it more difficult to guard against this attack.