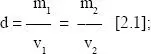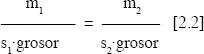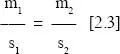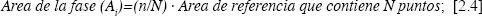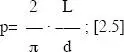José F. Pertusa Grau - Técnicas de análisis de imagen, (2a ed.)

El fundamento teórico del método de la pesada lo podemos encontrar fácilmente si aplicamos el concepto de densidad.

La densidad de una sustancia se define como la relación entre una determinada masa y el volumen que esta ocupa. La relación se mantiene constante sea cual sea la cantidad de sustancia considerada, por lo que si tomamos dos fragmentos cualesquiera del papel fotográfico (con masas m 1y m2 respectivamente), y suponiendo que la escasa cantidad de emulsión fotográfica no modifica sustancialmente la densidad, podremos expresar esa relación, para cada fragmento, de la siguiente manera:

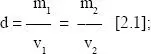
si calculamos los respectivos volúmenes (v 1y v 2) en función de la respectivas superficies tendremos que

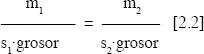
Sí eliminamos el término «grosor», la expresión queda justo como habíamos expuesto más arriba:

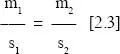
El método es tan ingenioso como laborioso porque, para darle validez estadística a los datos, se debía preparar un buen número de fotografías que habían de ser recortadas y pesadas. En estas circunstancias el trabajo final llegaba a ser importante, sin contar con el tedio que suponía la rutina general. Pero no podemos hacer otra crítica y tenemos que reconocer que se trata de un estimador del área muy aceptable.

2.2.4 Estimación del área por el método de la rejilla de puntos

La idea que subyace en el método de la pesada es que la fase más abundante en una foto ocupará mayor cantidad de área, por lo que la suma de los pesos de los trozos de papel que constituyen dicha fase será mayor que los pesos del resto de las fases. Lo mismo lo podemos enunciar en términos matemáticos diciendo que: «la probabilidad de que encontremos un trozo de hierro o carbón dependerá de su abundancia». O sea, que si dejamos caer al azar una minúscula gota de tinta sobre la fotografía de un acero, la probabilidad de que caiga sobre uno u otro componente dependerá únicamente de la abundancia de dicho componente. Pues bien, siguiendo ese principio, la determinación del área que ocupa una fase se puede ver desde un punto de vista probabilístico.

Si superponemos sobre la imagen una rejilla formada por puntos distribuidos regularmente, la cantidad de área que ocupa una determinada fase será proporcional al número de puntos (n) que caen sobre dicha fase. Si conocemos el total de puntos de la rejilla (N) y el área en la que se encuentran distribuidos (Área de referencia), el área de la fase se puede obtener por medio de una simple regla de tres. Es decir:

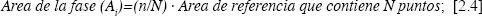
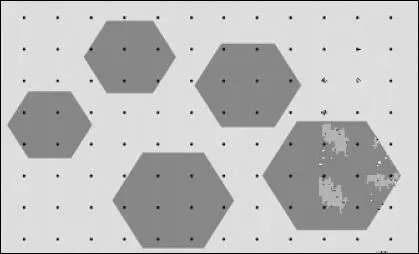
Fig. 2.2 Rejilla de puntos sobre una imagen.

El cociente n/N se conoce como fracción de área y es justamente la relación entre los puntos que caen sobre la fase de interés y los puntos totales que contiene el área de referencia. De ahora en adelante nos referiremos a la fracción de área, de forma abreviada, como A Ay su significado será el de: la proporción de área ocupada por la fase, o por un elemento, respecto al área de referencia; su valor se suele expresar en tantos por ciento.

El método es igualmente válido si se aplica una plantilla en la que el mismo número de puntos se encuentra repartido sin orden, en una distribución al azar. Se trata de una forma manual y simplificada del primitivo procedimiento denominado flaying spot (véase capítulo 3), en la que se ha predeterminado la situación de los puntos sobre la plantilla. Su aplicación se basa estrictamente en la aplicación del principio de probabilidad geométrica (véase capítulo 13).

La limitación principal para la utilización de plantillas con distribución regular o irregular de puntos está en que los objetos que pertenecen a la fase de interés se encuentren ordenados o no en la imagen. Esta afirmación casi resulta obvia si tenemos en cuenta que en una distribución regular de elementos pertenecientes a una misma fase, la ordenación de los puntos de la rejilla puede no coincidir nunca con los elementos de la fase o, por el contrario, que el número de coincidencias de puntos y estructuras de la fase sea excesivamente elevada. En ese caso se rompe la situación viciada utilizando una plantilla cuyos puntos se encuentren distribuidos aleatoriamente.

2.3 Estimación de la longitud

Uno de los parámetros que revistió más dificultad de cálculo, hasta que comenzó la aplicación del ordenador digital al análisis de imagen, fue la deter-minación de la longitud de un objeto. Se puede pensar que los objetos rectilíneos se miden fácilmente con una regla y que se puede calcular su longitud a escala real, multiplicando la medida obtenida por un factor de corrección. Pero, lamentablemente, las más de las veces los objetos suelen ser irregulares, con curvaturas, salientes y entrantes. En objetos muy estrechos solemos hablar de longitud, pero en la mayor parte de los casos hablamos de longitud y anchura. Incluso podemos hablar de determinar el perímetro, el cual se puede determinar como la longitud del borde que limita el objeto.

Para los objetos rectilíneos y estrechos, se pueden obtener buenos resultados utilizando una regla. También disponemos de un pequeño instrumento, el planí-metro, que nos permite obtener longitudes curvas y, por lo tanto, perímetros. Pero este instrumento ha ido cayendo en desuso y cada vez es más difícil encontrarlo en los laboratorios. Aunque los modernos sistemas de análisis de imagen han resuelto con sencillez el problema de la obtención de los principales diámetros de un objeto, la morfometría cuenta hace tiempo con un método que, como veremos, permite determinar longitudes de manera simple y efectiva.

2.3.1 El método de Buffon

Sea como fuere, el cálculo de la longitud de un objeto no parece, a primera vista, una cosa sencilla. Y no lo sería si no fuera porque Buffon 2 se hizo esa misma pregunta hace años y llego a proponer una solución tan simple como la que describimos más abajo.

Buffon planteó el problema de la medida de la longitud de unas agujas de igual tamaño. Postuló que, si se dejan caer las agujas al azar sobre una hoja en la que ha dibujado un conjunto de líneas paralelas equidistantes una distancia d, la probabilidad ( p) de que una aguja de longitud Ltoque una línea paralela es:

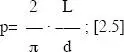
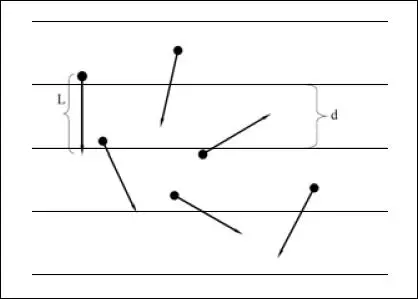
Fig. 2.3 Las agujas de Buffon.

Esto quiere decir que la probabilidad depende, de manera directa, del tamaño de las agujas y, de manera inversa, de la distancia entre las líneas paralelas. Ambas cosas resultan obvias porque es más fácil que se produzcan coincidencias cuando las líneas paralelas están separadas una distancia menor que la longitud de las agujas, que cuando las agujas sean muy pequeñas y la distancia entre las paralelas sea muy grande. Esto mismo lo hemos querido representar gráficamente en la fig. 2.4.