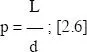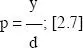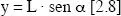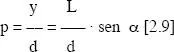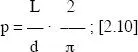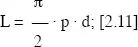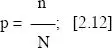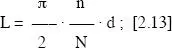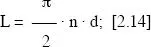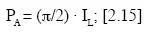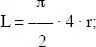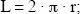José F. Pertusa Grau - Técnicas de análisis de imagen, (2a ed.)

Se puede llegar a la fórmula (2.6) de una manera muy simple. Una aguja cualquiera, perpendicular a las líneas paralelas tiene una probabilidad ( p) de intersección con cualquiera de ellas:

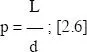
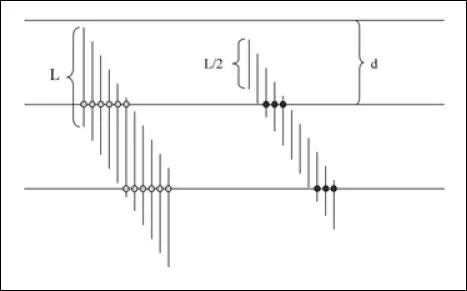
Fig. 2.4 Cálculo de intersecciones entre las paralelas de Buffón y dos conjuntos de líneas de longitud L y L/2 respectivamente. Es obvio que la probabilidad de intersección en el primer caso, el grupo de líneas de longitud L, será el doble que en el conjunto de longitud L/2.

Cuando la aguja no es perpendicular a las líneas de test, la probabilidad de intersección depende del ángulo (α) que formen entre sí. De hecho, la probabilidad de intersección en cualquier posición del segmento L se puede expresar en función de su proyección ( y) sobre un eje perpendicular a las líneas de test ( fig. 2.5):

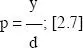
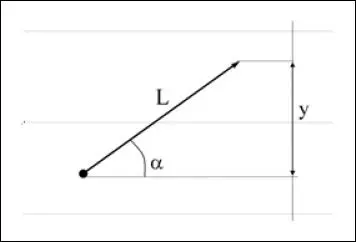
Fig. 2.5 Proyección de una aguja sobre el eje de ordenadas.

en donde la longitud de la proyección yse puede calcular como

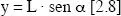
La probabilidad de intersección será entonces

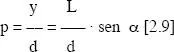
Para considerar todas las posibles orientaciones del segmento respecto a las líneas de test, debemos integrar la función (2.9) entre cero y 90 grados (π/2 radianes), lo que nos permite expresar la ecuación como:

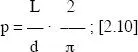
que es exactamente la ecuación (2.5).

Podemos utilizar a expresión (2.5) para despejar L. Así,

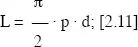
lo que quiere decir justo lo que acabamos de expresar más arriba, pero de forma matemática: la longitud de una aguja se puede calcular si conocemos un sistema de referencia de líneas paralelas y la probabilidad de que las líneas corten a las agujas cuando las dejamos caer al azar.

La probabilidad a la que nos estamos refiriendo una y otra vez tiene el sentido tradicional que todos conocemos; es decir, se trata de un estimador de cuántas veces se produce un evento concreto cuando se repite el ensayo un número determinado de veces. Tal vez el ejemplo paradigmático sea el de la moneda que se tira al aire: el evento favorable «sacar cara» tiene una probabilidad de que ocurra p=1/2, porque el total de eventos posibles, «cara» y «cruz», son solamente dos. La forma práctica de calcular experimentalmente esta probabilidad consiste en lanzar la moneda al aire una serie de veces (N) y anotar cuantas de estas veces sale cara (Vcaras), entonces la probabilidad es p =Vcaras/N y, si lo hemos hecho de manera correcta, el valor de esta probabilidad coincidirá con la expuesta arriba p=1/2.

Para el caso que nos ocupa, la probabilidad de que se produzcan cruces entre líneas paralelas y agujas se podría calcular tal y como lo hicimos con la moneda: si realizamos el experimento Nveces y el número de intersecciones agujas-conlíneas-paralelas es n, la probabilidad, p, se puede expresar como

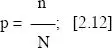
Si sustituimos esta expresión en la (2.11) podemos proponer una nueva ecuación:

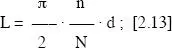
que nos permite estimar la longitud de las agujas de manera experimental, contando el número de intersecciones entre agujas y líneas paralelas.

Si realizados la medida una sola vez, N=1, la expresión se simplifica y queda:

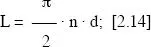
en donde el término (nd) es el número de intersecciones por línea (I L= nd).

Pero la aplicación de este procedimiento puede ir más allá del simple cálculo de las longitudes. Se puede aplicar para calcular el perímetro de una figura plana.

2.3.2 Cálculo del perímetro

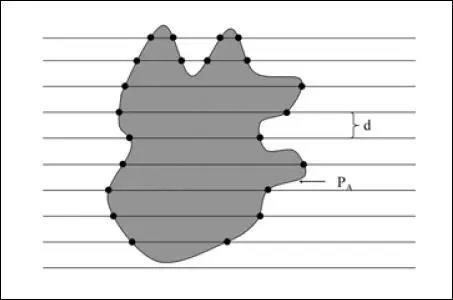
Fig. 2.6 Cálculo del perímetro de un elemento.

Si consideramos que el perímetro está formado por un conjunto de segmentos iguales, como hemos dicho antes, aplicando el mismo principio se puede escribir la expresión como

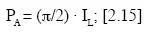
en donde I Les también el número de intersecciones de la línea que forma el perímetro con las paralelas separadas una distancia d.

Podemos demostrar la validez del método con un ejemplo: supongamos que se quisiera calcular el perímetro de una circunferencia de radio r. Si trazamos una serie de líneas paralelas separadas una distancia d=r, el número de intersecciones entre las líneas paralelas y la circunferencia será n=4 ( fig. 2.7). ¿Por qué n=4? Porque la circunferencia sólo puede caer de dos maneras entre las paralelas:

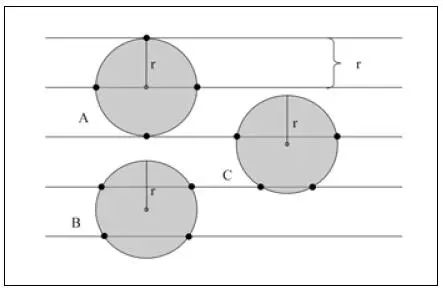
Fig. 2.7 Cálculo de la longitud de una circunferencia.

1 Si hacemos que una de las líneas paralelas sea tangente a la circunferencia, la siguiente línea cortará a la circunferencia por el mismo centro, y la siguiente paralela también será tangente a la circunferencia. Por lo tanto el número de puntos que intersecta será n=4: dos en las tangentes, más dos en la línea secante que pasa por el centro (fig. 2.7 A).

2 Si hacemos que la primera línea paralela sea secante a la circunferencia, la siguiente será secante también y el número de puntos también será n=4 (fig. 2.7 B y C).

Sustituyendo en la fórmula (2.14) obtendremos la siguiente expresión:

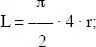
que simplificando queda

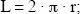
lo que resulta la bien conocida expresión de la longitud de una circunferencia.