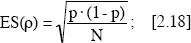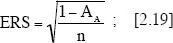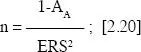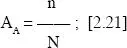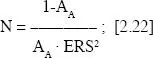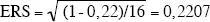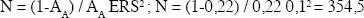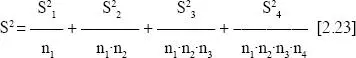José F. Pertusa Grau - Técnicas de análisis de imagen, (2a ed.)

Pero, ¿cómo obtenemos el error en el caso de la medida del área a partir del método de la rejilla de puntos? Es fácil pensar que la exactitud de este método del cálculo es más que discutible, dependiendo del tipo de rejilla que utilicemos.

En efecto, si se utiliza una rejilla con tan solo cuatro puntos, por ejemplo, y el objeto toca un único punto, el área del objeto sería igual a 1/4, independientemente del tamaño del objeto. Si, por el contrario, el objeto no toca ningún punto, el área será cero. Igualmente podemos ponernos en el otro extremo y pensar que para tomar una medida válida se necesitaría superponer una rejilla con tal cantidad de puntos que haría inviable la utilización del método.

Pero, como ya se puede suponer, siempre se puede llegar a una situación de compromiso en la que, estableciendo a priori un error tolerable, podamos superponer una rejilla con suficientes puntos como para que se pueda hacer viable el recuento.

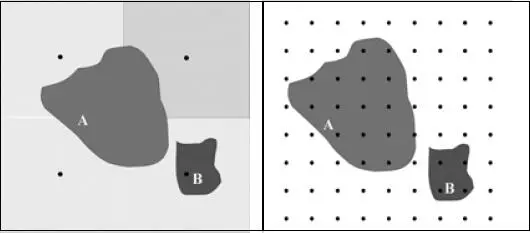
Fig. 2.9 Representación gráfica del efecto del número de puntos de la rejilla sobre la estimación de la fracción de área.

La estadística nos dice que la estimación de la fracción de área por medio del recuento de puntos presenta una distribución de tipo binomial, en la cual el error estándar de una proporción cualquiera ρ viene dada por la expresión:

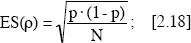
A partir de esta expresión, Hally 3 propuso una fórmula con la que calcular el error relativo estándar de la medida de la fracción de volumen, y que nosotros hemos adecuado a este problema:

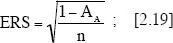
en la que AAes la fracción de área correspondiente n/N;

nes el número de puntos que contiene el objeto y

Nes el número de puntos totales de la rejilla.

Por lo tanto, haciendo una estima previa de la fracción de área con una rejilla cualquiera, podemos estimar cuál es el número idóneo de puntos totales de la rejilla para asumir un error máximo determinado.

Despejando n

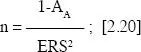
Y como

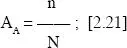
El número de puntos totales que debe tener la rejilla para obtener una fracción de área con un error relativo determinado, será:

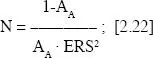
Un ejemplo ayudará a aclarar la utilidad de este apartado. Para ello vamos a utilizar la fig. 2.9.

De los 72 puntos (N = 72) que forman la rejilla, hay un total de 16 (n = 16) que caen en el interior del objeto A, por lo que su fracción de área A A= 16/72 = 0,22.

Aplicando la fórmula de Hally obtendremos un error relativo de

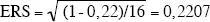
Lo que supone un error del 22,07 %, partiendo de una rejilla de 72 puntos.

Para calcular el tamaño de rejilla necesario para obtener la fracción de área con un error menor o igual al 10 % tendríamos:

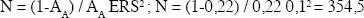
Esto es, deberíamos preparar una rejilla que contuviese más de 355 puntos, lo cual supondría que unos 78 puntos habrían caído dentro del objeto A.

Bien mirado no se trata de una rejilla excesivamente densa, aunque obtener la medida con precisiones mayores puede llegar a hacer imposible la preparación de una rejilla adecuada, y no digamos cómo de compleja podría ser la tarea de recuento de puntos.

2.4.3 El error experimental

El concepto de error en las ciencias experimentales tiene otras perspectivas, relacionadas con la heterogeneidad del universo de medida. El principal estimador de cualquier parámetro experimental es el valor promedio de las medidas realizadas, el cual se encuentra directamente relacionado con la variabilidad de la muestra. Para estimar la dispersión del promedio se calcula la desviación tipo, que se puede entender como el promedio de diferencias entre los valores obtenidos y la media.

Comúnmente se denomina error tipo a la diferencia promedio, porque el investigador utiliza este valor, entre otras cosas, para comprobar el grado de reproducibilidad de sus experimentos y, por lo tanto, comprobar si se han producido errores en la manipulación o el diseño de los experimentos.

No vamos a profundizar aquí sobre el análisis estadístico de los resultados porque creemos que el lector dispone de otras fuentes, más adecuadas que esta, para procesar adecuadamente sus datos. Pero sí queremos reflexionar sobre una cuestión que incide directamente sobre la forma de preparar las muestras para análisis de imagen y sobre el trabajo, en tiempo y esfuerzo, que conlleva realizar las medidas morfométricas.

La pregunta sería: ¿Es más precisa la determinación tomando muchas muestras de un solo individuo o tomando muchos individuos y muchas muestras por individuos? Una respuesta muy primaria sería que la virtud está en el punto medio y se deben tomar las muestras necesarias y suficientes. Pero si reflexionamos sobre nuestras condiciones experimentales sacaremos algunas conclusiones que pueden sernos de mucho provecho.

Supongamos que vamos a realizar un análisis del efecto que cierto tratamiento produce en el diámetro de los túbulos renales. Supongamos también que el primer paso en nuestro experimento es establecer el diámetro normal de los túbulos de los riñones control. Para ello disponemos de un riñón por cada n 1individuos normales que procesamos hasta obtener secciones histológicas en las que determinar las dimensiones de los túbulos en varios campos por sección. Buscando la máxima aleatoriedad en el muestreo, la preparación de las muestras sería:

a ) cada riñón se fragmenta en n 2rebanadas;

b ) de cada rebanada se preparan n 3bloques para cortar;

c ) de cada sección se recuentan n 4campos;

si denominamos S 2 ia la varianza en cada paso, la varianza global del experimento S2 se calcularía como:

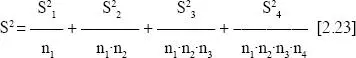
Parece claro que los denominadores de las fracciones son cada vez mayores, con lo que la contribución de cada fracción a la varianza global es cada vez menor. El término más significativo es precisamente el que depende del número de individuos que intervienen en la experiencia, como intuyen los experimentadores. Por ello debemos tener presente que el error disminuye más tomando mayor número de riñones que haciendo más recuentos por campo y riñón.