José F. Pertusa Grau - Técnicas de análisis de imagen, (2a ed.)

El método es más exacto cuando se aplica en el cálculo de perímetros curvos que cuando se utiliza para calcular el perímetro de formas angulosas. La imagen siguiente ( fig. 2.8) muestra la aplicación del método al cálculo del perímetro de un cuadrado y se puede comprobar el error que se introduce en estos polígonos. Conforme se incrementa el número de lados, tanto más se aproxima la figura a la circunferencia y más exacta es la determinación.

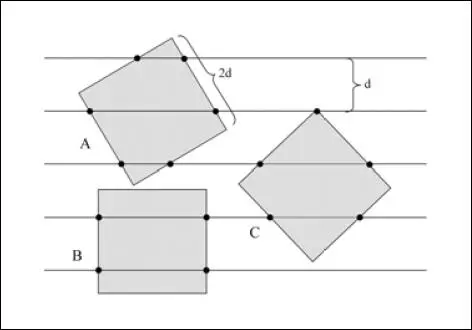
Fig. 2.8 Cálculo del perímetro de un cuadrado de lado 2d por el método de Buffón.

El criterio correcto de aplicación del método de Buffon es el mismo que rige en la obtención de cualquier magnitud: se debe calcular el perímetro varias veces, superponiendo cada una de ellas el sistema de paralelas al objeto haciendo que la superposición sea de forma aleatoria. La expresión de la medida será el promedio de cada una de las determinaciones y el error relativo será la desviación tipo.

En el ejemplo se muestran tres cuadrados iguales de lado 2ddispuestos sobre una serie de líneas paralelas separadas una distancia igual a d. Aplicando la fórmula del perímetro del cuadrado a este caso tenemos:

Si ahora aplicamos el principio de Buffon al cálculo del perímetro de cada uno de los cuadrados tendremos:

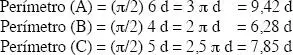
Es evidente que ninguno de los perímetros calculados coincide con el perímetro esperado porque, para que así fuese, el número de intersecciones de los cuadrados con las paralelas debiera ser aproximadamente de 5,095 y esto es, claramente, el promedio de intersecciones que se pueden obtener después de realizar la prueba un buen número de veces.

La conclusión es, como ya sabíamos, que se trata de un método basado en la probabilidad geométrica y que su exactitud también se encuentra sometida a las leyes de la estadística.

2.4 Errores de medida

2.4.1 Unidades de medida y errores

La preocupación por la exactitud de la medidas no es un asunto exclusivo de la morfometría sino que se trata de un problema de carácter general. El hombre desarrolló, cuando tuvo necesidad de ello, un sistema de pesas y medidas con el que resumir el mundo al número. Este hecho le permitió calificar los fenómenos y las cosas con una propiedad inherente a ellos mismos: sus dimensiones. El número revolucionó el pensamiento helénico y luego, gracias a los árabes, revolucionó el mundo renacentista. Aquella revolución ha llegado hasta nuestro tiempo, con las acotaciones pertinentes producto de cientos de años de experiencia en la obtención de las medidas de las cosas.

Cada comunidad había desarrollado un patrón de medida (tomemos la longitud como ejemplo), que había subdividido o ampliado para tratar de obtener las dimensiones de las cosas pequeñas y las grandes. En todos los casos, y para desespero de los científicos de la época, el objeto medido no solía contener un número exacto de veces el patrón de referencia. Esto ocurría siempre, aunque se subdividiese la unidad de medida una y otra vez. Además, cada individuo apreciaba de manera distinta cuántas veces se contenía la unidad de medida en el objeto al realizar la medida. Incluso cuando un mismo experimentador medía varias veces el mismo objeto, obtenía distintos valores en cada medida.

La física, que es la encargada de estos temas dimensionales, introdujo el concepto de error para explicar la limitación del patrón de medida y del experimentador. Así, la primera limitación, la falta de coincidencia de la unidad de medida con el objeto un número entero de veces, se podía salvar indicando el número de veces que se contenía la unidad de medida, más el número de fracciones de la unidad que aún era mayor el objeto (eso supone la invención de los números reales), pero añadiendo una coletilla donde se indicaba cuál era la fracción más pequeña en la que se había subdividido la unidad que se estaba utilizando. Esto se interpretaba como que la fracción de la unidad de medida no daba más de sí y que el objeto media, por lo tanto, más o menos esa cantidad fraccionaria. A ese último término le llamamos error absoluto y nos permite saber cuan fiable es el instrumento de medida del que nos servimos.

Para glosar con un ejemplo lo que acabamos de decir, queremos recurrir a una situación doméstica corriente: imagínense que van a comprar doce metros de cable eléctrico a la ferretería para construir un alargador para enchufar su nuevo ordenador a la red eléctrica. Todos esperamos que el dependiente nos corte un trozo de cable equivalente a doce veces una vara o una cinta de un metro de longitud. Pero imagínense que en la ferretería tienen una vara que mide cinco metros y que no esta subdividida de ninguna manera. Está claro que medirá con toda precisión cables que contenga la unidad de medida un número entero de veces, es decir, cinco, diez, quince metros. Incluso podrá medir, aunque con menos exactitud, siete metros y medio o doce metros y medio, lo que equivale a tomar la mitad de la vara, 2,5 metros, (aquí tendremos que fiarnos del buen ojo del dependiente). Todo lo que sea menor de esa medida tomada con esa unidad será un intento de aproximación a la longitud de cable, tanto más dudoso cuanto más se aleje de la fracción 2,5 metros.

Afortunadamente, en lo cotidiano no llegamos a encontrarnos dependientes con tan mala unidad de medida, sino que las tiendas cuentan con unidades de un metro, divididas en cien fracciones (centímetros). Seguramente podremos adquirir doce metros de cable, centímetro arriba, centímetro abajo. Esto se puede expresar como 12,00 ± 0,01 metros, lo que se lee como «doce metros, más o menos un centímetro».

No obstante, el error que se comete midiendo el cable con una barra de un metro de longitud (tomando doce unidades para completar los doce metros) es mayor que el error que se comete si utilizamos una cinta de doce metros y se realiza la medida de una sola vez, porque los errores de medida son aditivos.

Si compramos dos trozos de cable en dos tiendas distintas, pidiendo en cada caso la misma longitud de cable, y los comparamos cuidadosamente, comprobaremos que uno es más largo que el otro. ¡Aunque cada dependiente se haya tomado el mismo interés en realizar la medida! El experimentador sabe que, por muy bueno que sea el instrumento, la medida del objeto no la obtiene nunca de forma exacta, sino que se aproxima a ella tanto más cuanto más veces se realice la misma.

Ambos errores son insolubles y hoy han entrado a formar parte de lo que llamamos condiciones de la medida.

Una cuestión casi obvia es la relatividad del error; esto es, la relación entre el error absoluto y la medida a obtener. Es una forma de indicar lo ajustado de la medida: siempre será más precisa la medida del cable de doce metros determinada con un error de un centímetro, que la medida de un cable de medio metro con el mismo error. Denominamos error relativo al cociente entre el error absoluto y la magnitud medida.

2.4.2 Precisión del método en función del número de puntos de la rejilla

El error relativo de una medida depende del error absoluto, digamos del error intrínseco del instrumento de medida, y de la magnitud obtenida. Su cálculo es muy simple cuando utilizamos una regla, dividida en milímetros, con la que medimos la longitud del cable alargador; el error absoluto será igual a 0,01 metros, mientras que el error relativo se obtendrá del cociente