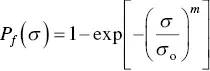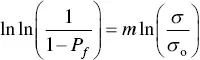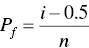Mohamed N. Rahaman - Materials for Biomedical Engineering

where, σ yis the yield stress, σ ois the yield stress for the easiest slip system in a single crystal, and G is the grain size of the polycrystalline metal. Thus, reduction of grain size provides a powerful method to enhance the yield stress of metals ( Chapter 6). Equation (4.35)can be derived theoretically by assuming that dislocations pile up at the grain boundaries that provide obstacles to dislocation motion. As the grain size decreases, the number of boundaries per unit volume increases, providing a larger number of obstacles.

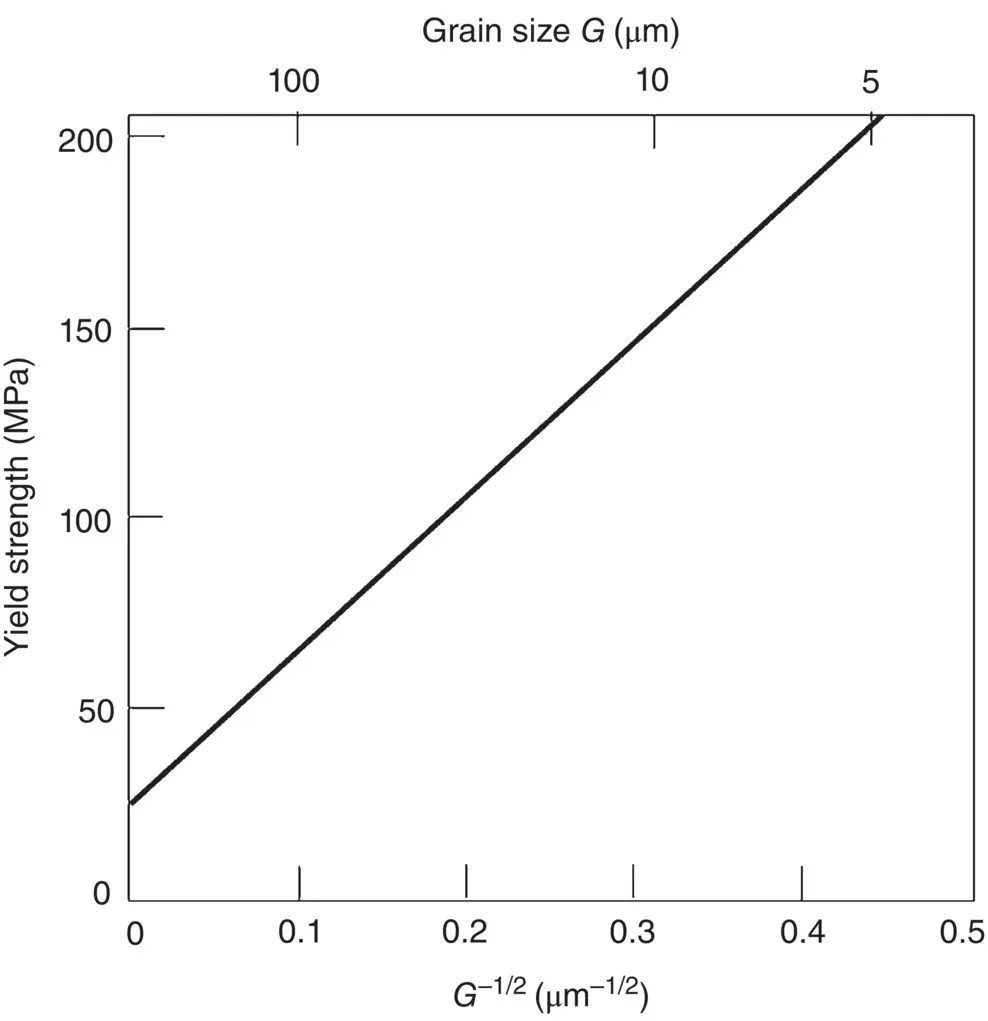
Figure 4.14 The influence of grain size on the yield strength of a 70Cu–30Zn brass alloy.

Source: From Callister (2007) / with permission of John Wiley & Sons.

The effect of grain size on the strength of brittle ceramics is more complicated than that for ductile metals. This is because the strength of brittle materials is strongly influenced by the presence of flaws such as microcracks, particularly those at their surface ( Section 4.4.2). For ceramics composed of grains of size smaller than ~10–20 μm, the flaw size is often larger than the grain size and, consequently, the strength of these ceramics should be independent of the grain size. However, data for ceramics often do show an increase in average strength with decreasing grain size below 10–20 μm. Although there is a wide scatter in the data due to various degrees of surface finish of the specimens prior to testing, the average flexural strength of alumina, the most widely studied ceramic, shows an increase from ~400 MPa to ~600 MPa with a decrease in grain size from 10 to 1 μm (Wachtman et al. 2009).

An understanding of mechanical property principles is important in designing materials for use in biomedical applications and engineering applications as well. These principles are particularly important in applications where the biomaterial is subjected to a significant stress, such as fracture fixation plates, total joint replacement, healing of large defects in the long bones of the human limbs and dental restorations such as crowns and bridges.

A common requirement in the design of some biomaterials is that their shape and dimensions should remain constant. For ductile metals and alloys, this means that while plastic deformation might occur locally at a few specific points, such as the vicinity of a microvoid, it should not spread throughout the entire material. Consequently, the highest stress that the metal is subjected to should be less than its measured yield stress. As the fracture of ductile metals is considerably less sensitive to the presence of microstructural flaws such as pores and microcracks when compared to brittle ceramics, the average value of their measured yield stress is a useful design property.

The design requirements for ceramics are often more complex than those for metals. These requirements should be recognized because brittle fracture of an implant in vivo is a serious complication. In general, the measured strength of a number of nominally identical ceramic specimens often shows considerable scatter because the size, position, and orientation of flaws such as microcracks vary from one specimen to another ( Section 4.2.5). This has important consequences for design. As failure at any flaw can lead to failure of the entire specimen, the strength that can be safely used in design is often far lower than the average measured strength. A specimen size effect also has to be taken into account because there is a higher probability of a strength‐determining flaw present in a larger volume. Another factor is that the measured strength depends on the testing technique because each technique subjects a different volume of the specimen to a tensile stress. In order to account for all of these factors quantitatively, the design of brittle materials such as ceramics and glasses is often treated by a statistical method called Weibull statistics.

Weibull statistical analysis employs a weakest link assumption that failure of a single element of the specimen results in failure of the entire specimen. Instead of the more common distribution functions used to describe experimental data, such as the normal distribution, Weibull analysis assumes a function, called the Weibull distribution, to describe the measured strength of brittle materials. One form of the distribution, called the two‐parameter distribution, is

(4.36)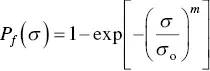

where, P f( σ ) is the cumulative probability of failure, that is, the probability that failure has occurred by a stress σ, m is the Weibull shape parameter, a number often called the Weibull modulus, which is an inverse measure of the width of the distribution, that is, a higher value of m corresponds to a narrower distribution, and σ ois the Weibull scale parameter, a measure of the center of the distribution, equivalent to the probability of failure occurring at or below a stress σ ois 0.63.

Weibull analysis of experimental data starts with measuring the strength of ~30 or more specimens in a given loading mode such as bending or compression using a standard procedure. Then the data are fitted, often using a least‐squares method, by the Weibull distribution. Taking the natural logarithm twice of Eq. (4.36), we get

(4.37)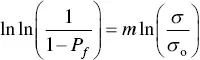

The Weibull parameters m and σ oare determined by fitting a straight line to a plot of the left‐hand‐side of Eq. (4.37)versus ln σ for the measured data. The general procedure for determining P ffrom the data is to assign a rank to each value of the measured strength after sorting in an ascending order, by assigning a rank of 1 to the lowest value and n to the highest value. The failure probability assigned to the i th strength value is

(4.38)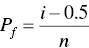

As an example of fitting strength data to obtain the Weibull parameters, Figure 4.15shows data for porous bioactive glass specimens with a uniform grid‐like microstructure (similar to that shown in Figure 3.24b). The data were obtained by measuring the strength of 30 or more nominally identical specimens each, in their as‐fabricated state, in compression and in bending (Liu et al. 2013). Data taken from the literature for hydroxyapatite and β‐tricalcium phosphate specimens with a similar microstructure, tested in compression only, are shown for comparison. For the purpose of comparison, the data for the different materials are presented as a double logarithmic plot of ln[1/(1− P f) versus σ , instead of a plot represented by Eq. (4.37).

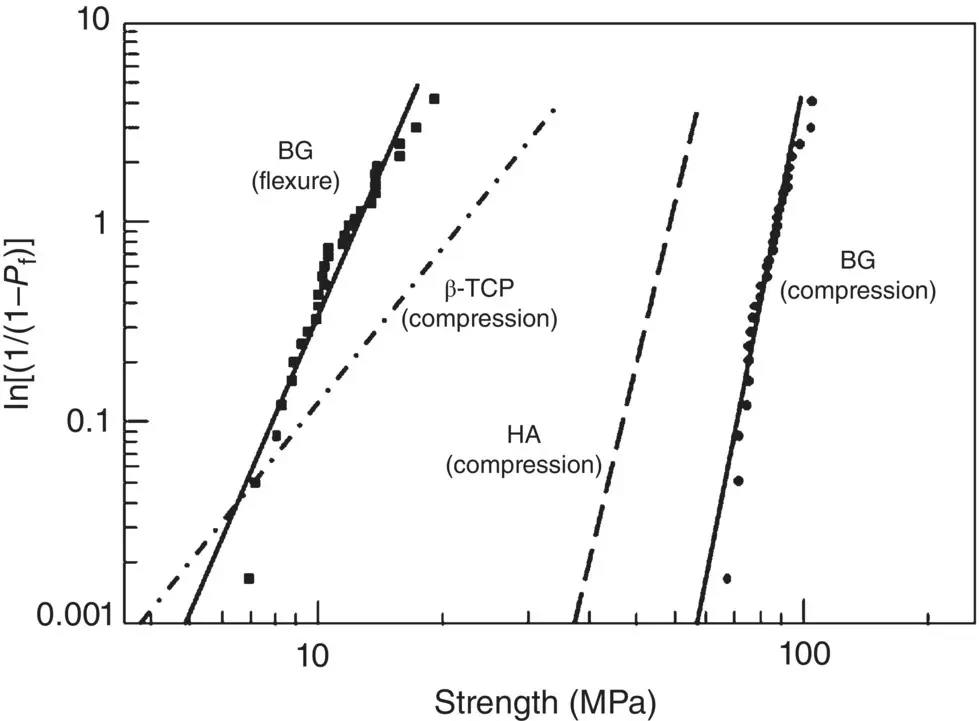
Figure 4.15 Weibull plots for porous bioactive glass (BG) specimens in compression and flexural loading. Data for hydroxyapatite (HA) and β‐tricalcium phosphate (β‐TCP) specimens with a similar microstructure are shown for comparison.