Mohamed N. Rahaman - Materials for Biomedical Engineering
Здесь есть возможность читать онлайн «Mohamed N. Rahaman - Materials for Biomedical Engineering» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Materials for Biomedical Engineering
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:4 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
- 80
- 1
- 2
- 3
- 4
- 5
Materials for Biomedical Engineering: краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Materials for Biomedical Engineering»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
A comprehensive yet accessible introductory textbook designed for one-semester courses in biomaterials Materials for Biomedical Engineering: Fundamentals and Applications
Materials for Biomedical Engineering: Fundamentals and Applications
Materials for Biomedical Engineering — читать онлайн ознакомительный отрывок
Ниже представлен текст книги, разбитый по страницам. Система сохранения места последней прочитанной страницы, позволяет с удобством читать онлайн бесплатно книгу «Materials for Biomedical Engineering», без необходимости каждый раз заново искать на чём Вы остановились. Поставьте закладку, и сможете в любой момент перейти на страницу, на которой закончили чтение.
Интервал:
Закладка:
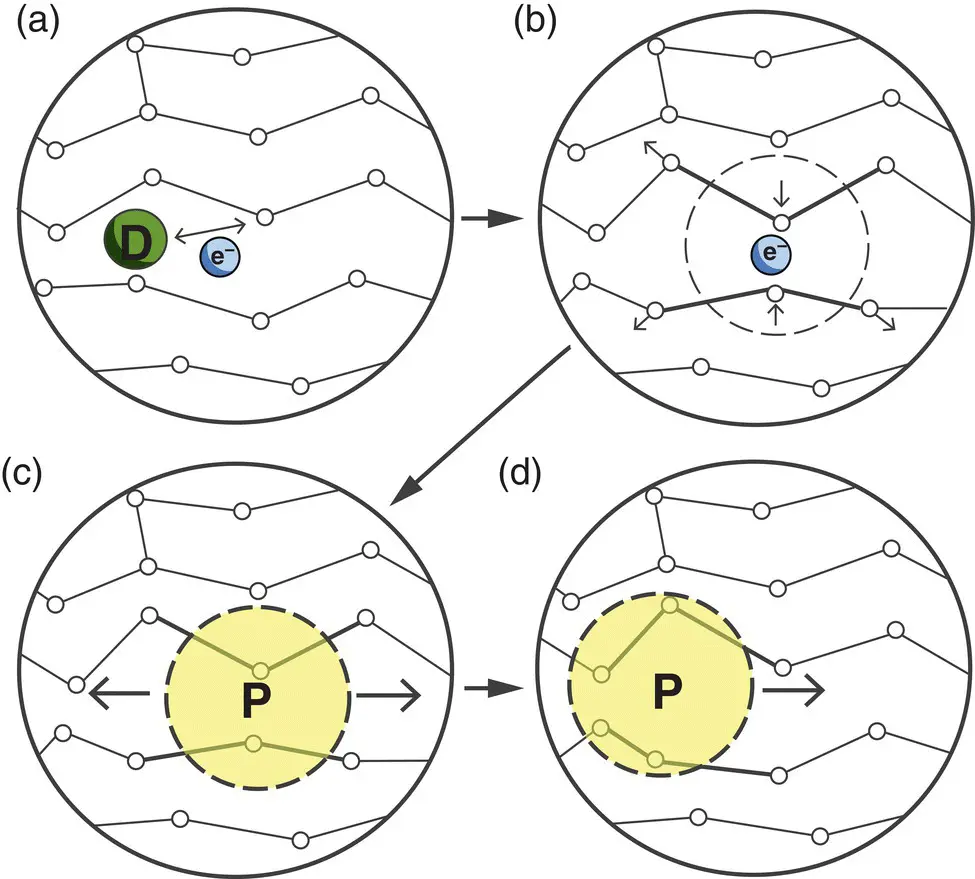
Figure 4.17 Simplified explanation of the electrical conductivity of conducting polymers. (a) A dopant D removes or adds an electron from/to the polymer chain, creating a delocalized charge. (b) It is energetically favorable to localize this charge and surround it with a local distortion of the crystal lattice. (c) A charge surrounded by a distortion is known as a polaron P (a radical ion associated with a lattice distortion). (d) The polaron can travel along the polymer chain, allowing it to conduct electricity.
Source: From Balint et al. (2014).
4.6 Magnetic Properties
Magnetic properties have not traditionally played an important role in the development of biomaterials but the interesting and improved properties observed for nanoparticles and nanostructured materials have generated considerable interest in the use of magnetic nanoparticles for biomedical applications. Magnetic nanoparticles are being considered for a variety of biomedical applications such as drug delivery, hyperthermia treatment of tumors and contrast agents for magnetic resonance imaging (Pankhurst et al. 2003).
Magnetism is commonly viewed as an attraction or repulsion between two materials. Whereas all materials are magnetic to some extent, the magnetism that we know from daily experience, such as iron filings or nails attracted to a bar magnet, is an important but special type of magnetic behavior called ferromagnetism. This type of magnetism is relevant to biomedical applications of magnetic nanoparticles and to engineering applications as well but there are weaker forms of magnetism called paramagnetism and diamagnetism. These different types of magnetism have their origins in the atomic structure of the constituent atoms or ions of the material. It is useful to understand how they arise in order to control or improve the magnetic properties of materials used as biomaterials.
4.6.1 Origins of Magnetic Response in Materials
The magnetic response of a material depends on its atomic structure and, in the case of some materials, on its temperature, although the effect of temperature is not normally relevant to the application of biomaterials. We can view a magnet as a dipole with a certain magnetic moment in much the same way as we view an electric dipole with an electric dipole moment ( Chapter 2). The magnetic response of a material has its origins in the tiny magnetic dipole moments associated with the individual electrons of its constituent atoms or ions.
There are two contributions to the magnetic dipole moment of the electron ( Figure 4.18). One is due to the intrinsic spin of the electron analogous to a charged body spinning about its own axis. The other is due to its orbital motion around the nucleus. Each contribution is quantized, that is, it depends on
The spin quantum number ms of the electron, which can have values of +1/2 (sometimes referred to as spin up) and −1/2 (spin down)
The magnetic orbital quantum orbital quantum number ml of the electron, which can have values from −l to +l, where l is the angular momentum (azimuthal) quantum number.
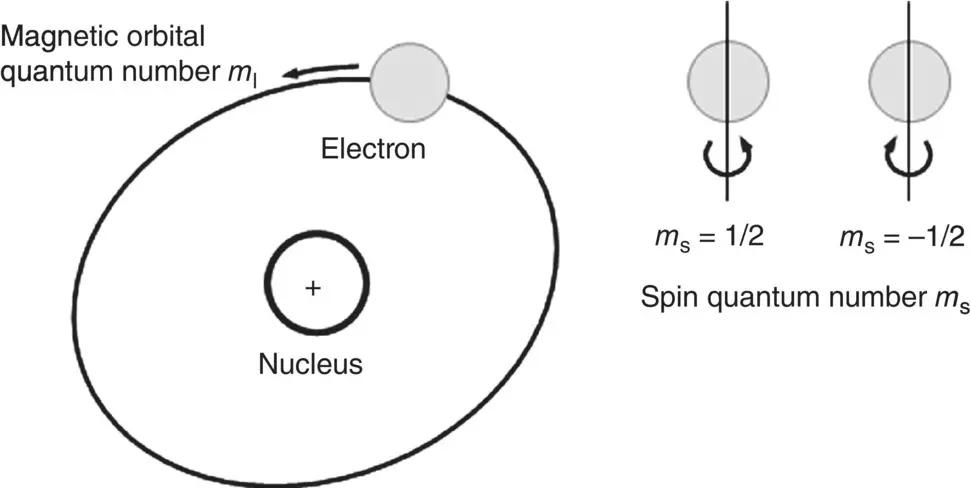
Figure 4.18 Schematic diagram illustrating the two contributions to the magnetic dipole moment of an electron in an atom due to its intrinsic spin and its orbital motion around the nucleus.
The important quantity is the Bohr magneton μ B, the magnetic moment of an unpaired electron, equal to 9.27 × 10 −27J/T. For each electron in an atom, for example, the intrinsic spin magnetic moment is +μ B(spin up) or −μ B(spin down), whereas the orbital magnetic moment is m lμ B.
4.6.2 Meaning and Definition of Relevant Magnetic Properties
If a magnetic material is placed in an applied magnetic field of strength H , the individual atomic magnetic moments contribute to its overall response such that the internal field strength B in the material, also called the magnetic induction or magnetic flux density, is given by
(4.40) 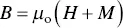
where, μ ois a physical constant called the permeability of free space (equal to 1.257 × 10 −6H/m) and M is the magnetic moment per unit volume of the material, commonly referred to as its magnetization. B , H , and M are vectors but to simplify the discussion, we will not emphasize this point and just consider their magnitude. As the magnetic flux density in a vacuum B ois equal to μ o H , the term μ o M represents the change in the flux density due to the presence of the material.
A few different parameters are used to classify the magnetic properties of magnetic materials. The magnetic susceptibility χ m, defined by
(4.41) 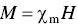
relates the magnetization induced in a material by an applied field H . As both M and H have the same units (A m), χ mis unitless, that is, a number without units. The relative permeability μ ris defined as
(4.42) 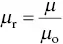
where, μ is the permeability of the material. The susceptibility or the relative permeability provides a measure of the degree to which a material can be magnetized by an applied field. They are related by
(4.43) 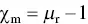
4.6.3 Diamagnetic and Paramagnetic Materials
For most atoms (or ions), the magnetic effects of the electrons, including their spin and orbital motions, cancel out and, consequently, the atom is not magnetic. This is true for atoms of the inert gasses and atoms of elements such as zinc that have completely filled electron shells. The Pauli exclusion principle requires that two electrons in any energy level of an atom must have opposite spins and, thus, the resultant spin magnetic moment of paired electrons is zero. Materials composed of atoms in which all the electrons are paired have no intrinsic magnetic moment and are described as diamagnetic. A weak magnetic dipole may be induced in these materials when they are placed in a magnetic field but the induced dipole points in a direction opposite to that of the field.
On the other hand, for other atoms or ions such as those of some transition elements, the magnetic effects of the electrons do not cancel, since one or more unpaired electrons are present, and the atom as a whole has a magnetic moment. In the absence of an applied magnetic field, the orientations of the atomic dipoles are random and, thus, the material as a whole has no net magnetic moment. However, when placed in an applied magnetic field, the atomic dipoles line up in the direction of the applied field. This type of magnetic behavior is referred to as paramagnetism.
Diamagnetic materials have χ mvalues in the range approximately −10 −6to −10 −3, whereas paramagnetic materials have χ mvalues in the range ~10 −6to 10 −1. The susceptibility of diamagnetic materials is negative whereas it is positive for paramagnetic materials. This is because in an applied magnetic field, the induced atomic dipoles in a diamagnetic material point in a direction opposite to the magnetic field, making the field within the material lower than that of a vacuum. On the other hand, the atomic dipoles present in a paramagnetic material line up in the direction of the applied field, in much the same way as a compass needle lines up in the earth’s magnetic field. This has the effect of increasing the magnetization of the material.
Читать дальшеИнтервал:
Закладка:
Похожие книги на «Materials for Biomedical Engineering»
Представляем Вашему вниманию похожие книги на «Materials for Biomedical Engineering» списком для выбора. Мы отобрали схожую по названию и смыслу литературу в надежде предоставить читателям больше вариантов отыскать новые, интересные, ещё непрочитанные произведения.
Обсуждение, отзывы о книге «Materials for Biomedical Engineering» и просто собственные мнения читателей. Оставьте ваши комментарии, напишите, что Вы думаете о произведении, его смысле или главных героях. Укажите что конкретно понравилось, а что нет, и почему Вы так считаете.












