Mohamed N. Rahaman - Materials for Biomedical Engineering

Diamagnetism and paramagnetism are weak forms of magnetism and, consequently, materials that show these two types of behavior are often considered nonmagnetic. Certain materials that contain paramagnetic atoms or ions, however, do show a strong permanent magnetization even in the absence of a magnetic field. This type of response, called ferromagnetism, is shown by materials composed of atoms of certain transition elements such as iron and cobalt, and certain rare earth elements such as gadolinium. In ferromagnetic materials, a special type of coupling occurs between adjacent atoms, resulting in cooperative alignment of their magnetic moment throughout the crystal. This coupling is purely a quantum mechanical effect that cannot be adequately explained in terms of classical physics. It leads to a high net magnetic moment of the material even in the absence of a magnetic field. Ferromagnetism is a property not just of the individual atoms but is a result of the interaction of each atom with its neighbors in the crystal lattice of the solid. Although the magnetization can vary with the magnetic field, magnetic susceptibility χ mvalues as high as 10 6are possible for ferromagnetic materials.

Another property of ferromagnetism is that each grain in a polycrystalline material (or the whole crystal of a single crystalline material) is made up of a number of magnetic domains, tiny regions in which the atomic dipoles are essentially perfectly aligned. These domains are originally oriented in such a way that they cancel each other as far as their external magnetic effects are concerned ( Figure 4.19a). However, when a ferromagnetic material is subjected to an applied magnetic field of gradually increasing strength, the domains that are favorably oriented grow at the expense of those that are not, and the material becomes highly magnetized ( Figure 4.19b).

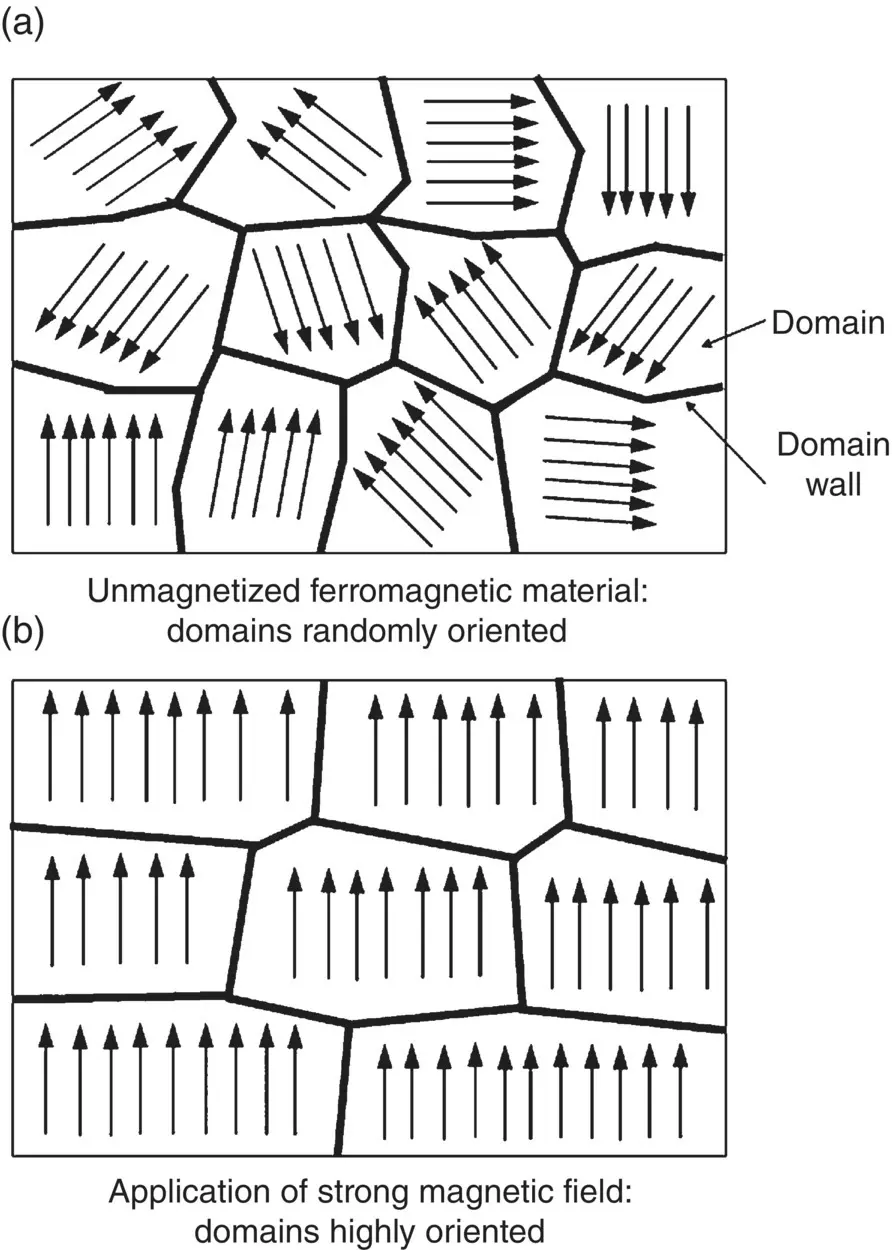
Figure 4.19 Schematic illustration of magnetic domains in a ferromagnetic material: (a) Randomly oriented domains in an unmagnetized material. (b) The domains become oriented upon application of a magnetic field, resulting in a highly magnetized material. Each arrow represents a huge number of atoms.

The maximum possible magnetization of a ferroelectric material, called the saturation magnetization M max, corresponds to the magnetization that would result if all the atomic dipoles of the material were completely aligned with the magnetic field. There is also a saturation magnetic flux density, B max( Eq. (4.40)). For the transition metal atoms (those with a partially filled d electron subshell), the contribution from the orbital angular momentum is negligible and, thus, the magnetic moment of the atom is determined by the number of unpaired electrons. Consequently, in the transition metals where the 3d shells of the atoms are partially filled, we can determine the magnetic moment of the atoms by filling the 3d shell with aligned spins up to a maximum of five beyond which the spins must have an opposite or antiparallel alignment to the first five. This is required by the Pauli exclusion principle. In the iron (Fe) atom, for example, the net number of unpaired electrons is four and, thus, the net magnetic moment of the atom is 4 μ B, where μ Bis the Bohr magneton. Experimental magnetization curves of M (or B ) versus H show a saturation magnetization that is lower than the ideal value due to microstructural factors and pinning of the domain walls by defects such as grain boundaries.

Another type of magnetism, called ferrimagnetism, more common in ionic‐bonded ceramics, refers to a type of ferromagnetism in which the magnetic moment of ions at one type of atomic sites is partly cancelled by antiparallel interactions with ions of another site. However, there remains a net magnetic moment of the material in the absence of a magnetic field. Ferrimagnetic ceramics have a lower saturation magnetization than ferromagnetic metals but their electrically insulating properties provide an advantage in some engineering applications where a low electrical conductivity is required.

The ferrimagnetic iron oxides Fe 3O 4, commonly referred to as magnetite, and ferric oxide, γ‐Fe 2O 3, referred to as maghemite, are the most widely studied nanoparticles for hyperthermia treatment of tumors because of their favorable biocompatibility. Magnetite has a crystal structure that belongs to a class of compounds called spinels. The formula of normal spinels has the general formula AB 2O 4(or AO∙B 2O 3), where A 2+and B 3+are divalent and trivalent ions, respectively. These normal spinels have a characteristic crystal structure based on a close packed face‐centered cubic (FCC) lattice of O 2−ions, with the A 2+ions and B 3+ions occupying tetrahedral and octahedral interstitial sites within the lattice. Magnetite has an inverse spinel structure B(AB)O 4in which the occupancy of the interstitial sites is slightly different. One‐half of the B 3+ions in magnetite occupy tetrahedral sites (called a sites) whereas the A 2+ions and remaining half of B 3+ions occupy octahedral sites (called b sites) ( Figure 4.20a). In magnetite, the O 2−ions are nonmagnetic due to all their electrons occupying filled shells. Consequently, we need to consider only the interactions between one‐half of the Fe 3+ions (with five unpaired electrons in their 3d shell) on the a sites and the Fe 2+ions (four unpaired electrons in their 3d shell) and the other half of the Fe 3+ions on the b sites ( Figure 4.20b). The antiparallel a–b interaction between the ions in the a and b sites dominates and, thus, the saturation magnetization per formula unit (Fe 3O 4) is 4 μ B.

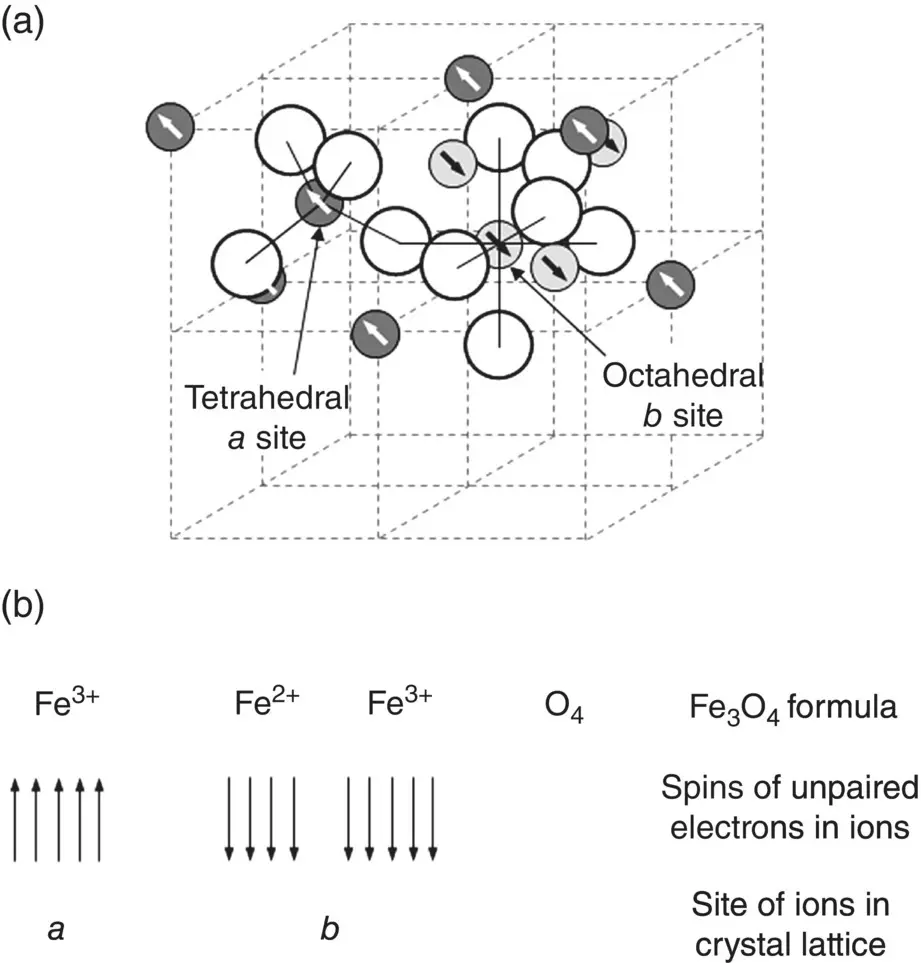
Figure 4.20 (a) Part of Fe 3O 4crystal structure showing the tetrahedral a sites and octahedral b sites. (b) Illustration showing the arrangement of the electron magnetic moments of the Fe ions at the a and b sites in the Fe 3O 4crystal structure.

Maghemite (γ‐Fe 2O 3) has the same crystal structure as magnetite but it is often considered a ferrous ion (Fe 2+) deficient magnetite because there are no Fe 2+ions in the crystal structure when compared to magnetite. Although there is no clear agreement about the distribution of the cations in the maghemite crystal structure, it is often stated that the Fe 3+ions occupy both the tetrahedral a sites and octahedral b sites, with five Fe 3+ions and one vacancy in the b sites for every three Fe 3+ions in the a sites. This can be expressed by the formula Fe[Fe 5/3◻ 1/3]O 4where the symbol ◻ represents a vacant site.

Measured curves of magnetization M versus applied magnetic field H (or magnetic flux density B vs H ) for diamagnetic and paramagnetic materials are straight lines and they retrace themselves as H is increased or decreased. In comparison, magnetization curves for multi‐domain ferromagnetic and ferrimagnetic materials are not straight lines and they do not retrace themselves as H is increased or decreased ( Figure 4.21). This lack of reversibility is a well‐known phenomenon called hysteresis. Another feature of the magnetization curves for ferromagnetic and ferrimagnetic materials is that they show a remanent magnetization (point C or point D) even though there is no applied field. This is the phenomenon of permanent magnetism. Hysteresis is due to the presence of multiple magnetic domains within the material. The motion of the domain boundaries and the reorientation of the domain directions are not fully reversible. The domains do not return completely to their original arrangement but, instead, some alignment of the magnetic dipoles remains even when the magnetic field is completely removed.