Theoretical Analysis of Brittle Fracture
A criterion for fracture of brittle solids could be developed by determining the stress at a sharp crack tip and equating it to the theoretic strength. However, this is challenging because it requires detailed consideration of the atom arrangement at the crack tip. Instead, a widely recognized theory of fracture in brittle solids, called the Griffith theory, is based on energy considerations and assumes that the solid is a continuum, thus neglecting atomic considerations of the fracture process. An energy balance concept is assumed such that the limiting condition for crack growth occurs when the energy released by the elastic strain energy is equal to the energy required to create new crack surface. The analysis typically assumes a model composed of a thin wide plate containing a long thin elliptical‐shaped crack of length 2 c through it which is subjected to a tensile stress σ in the direction perpendicular to the length of the crack ( Figure 4.9). For this model, the theory predicts that fracture will occur when the stress at the crack tip becomes equal to σ f, called the fracture stress, given by
(4.24) 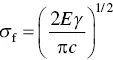
where, E is the Young’s modulus and γ is the surface energy per unit area of the solid. Equation (4.24), commonly called the Griffith equation, is often taken as a necessary condition for fracture to occur. As the surface energy of many ceramics falls within a narrow range, ~0.5–2.0 J/m 2, Eq. (4.24)can be seen to provide theoretical underpinning for the strong effect of microstructural flaws on their tensile strength.
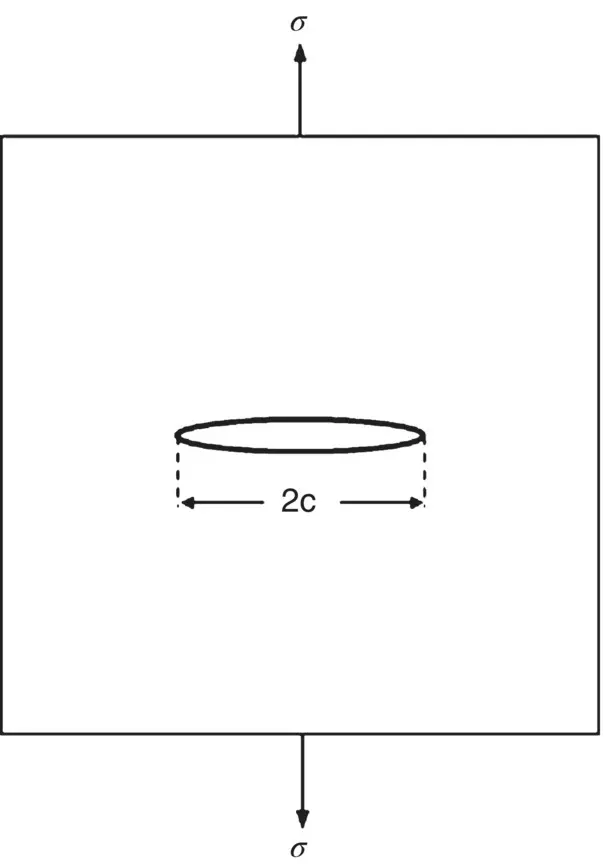
Figure 4.9 Geometrical model used in the Griffith theory of brittle fracture.
Equation (4.24)is often written
(4.25) 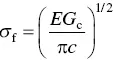
where, G cis called the toughness, equal to 2 γ ( Section 4.2.6). Thus, we can say that brittle facture will occur when
(4.26) 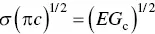
According to Eq. (4.26), fracture will occur when, for a material subjected to a stress σ , a crack reaches a certain critical size c or, alternatively, when a material containing cracks of size c is subjected to some critical stress σ . The term on the left‐hand‐side of Eq. (4.26)occurs frequently in fracture mechanics and is often referred to as the stress intensification factor K . Thus, we can also say that fracture will occur when K = K cwhere K cis called the critical stress intensification factor or more commonly, the fracture toughness, given by
(4.27) 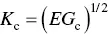
Using Eqs. (4.26)and (4.27), the tensile strength is given by
(4.28) 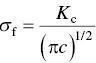
Brittle materials do not contain just one crack but many cracks that differ in size. In tension (or flexure), fracture occurs typically by rapid propagation of the largest crack of length 2 c . On the other hand, fracture in compression typically occurs less rapidly by extension of many cracks. Thus, the fracture strength in compression is given as
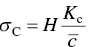
where, H is ~10 and 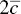 is the average crack length.
is the average crack length.
4.2.6 Toughness and Fracture Toughness
Toughness refers to the ability of a material to withstand rapid propagation of a crack through it. The toughness G cof a material is defined as the energy absorbed per unit area of crack (units J/m 2). A high G cmeans that it is difficult for a crack to propagate through a material, as in pure ductile metals such as aluminum and copper, for example, which have G cvalues in the range 100–1000 kJ/m 2. In comparison, brittle materials such as ceramics have low G cvalues, in the range 0.01–0.1 kJ/m 2, and, thus, it is easy for cracks to propagate through them.
The toughness of a material is difficult to measure and, consequently, more easily measured parameters are used to provide a measure of toughness. One such parameter is the area under the stress–strain curve in a given loading mode such as tension or flexure ( Figure 4.10). This area can be used to compare the relative toughness of specimens with a similar geometry but it is not equal to the toughness G cof the material. As Figure 4.10indicates, there is often no correlation between strength and toughness. The area under the elastic region of the stress–strain curve is often referred to as the resilience because it gives a measure of the energy recovered upon unloading a specimen.
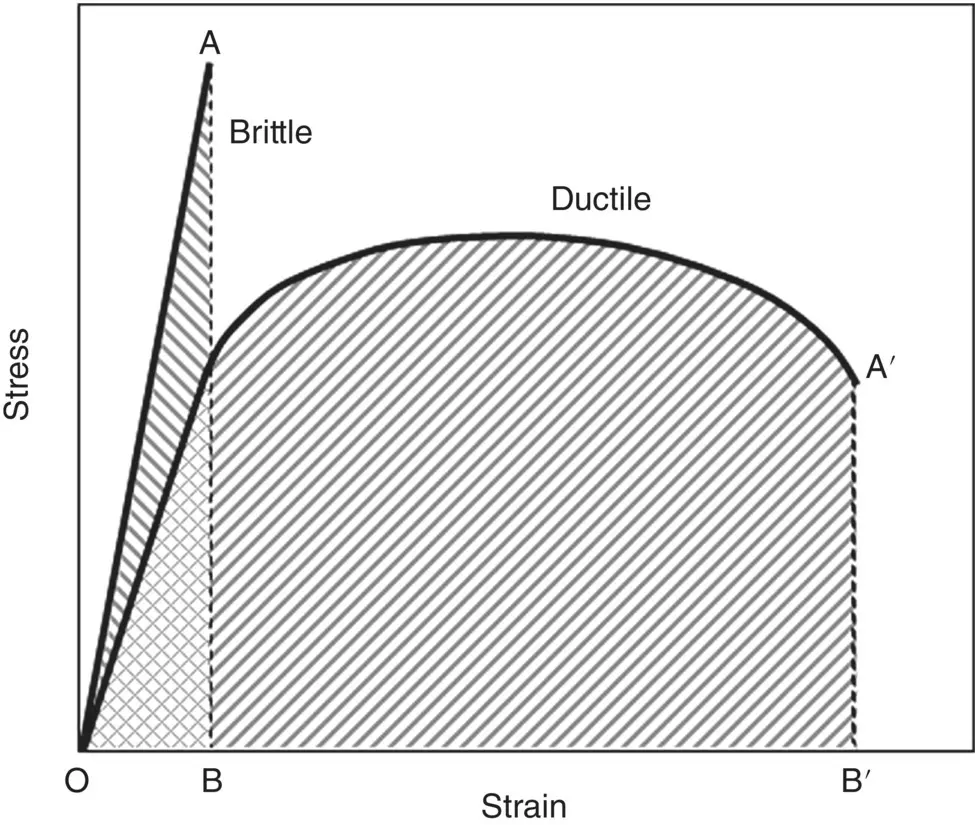
Figure 4.10 Area under the stress–strain curve used as measure of the relative toughness between materials of the same geometry.
A more widely used parameter of toughness is the fracture toughness K c. It is determined experimentally using standard techniques by inserting a crack of length c into a specimen and loading it until fracture occurs. K c(units MN/m 3/2or MPa m 1/2) is related to G cby Eq. (4.27).
Pure metals have K cvalues in the range ~100–350 MN/m 3/2( Table 4.1). The K cvalues of the majority of ceramics and glasses are in the range ~0.5–5 MN/m 3/2. On the other hand, a few ceramics such as YSZ and silicon nitride (Si 3N 4) can have K cvalues equal to ~10 MN/m 3/2. The higher fracture toughness of YSZ is due to the occurrence of a phase transformation in the region of the crack tip, which dissipates some of the energy available for crack propagation. This process is described as transformation toughening ( Chapter 7). On the other hand, a unique fibrous structure of elongated grains coupled with an appropriate thin glass phase at the grain boundaries is responsible for the higher fracture toughness of Si 3N 4. A crack propagates along the weaker glass phase at the grain boundaries, making the crack path more tortuous when compared to a straighter path directly across the grains. This tortuous path consumes more energy than a straighter path. Polymers have G cvalues between those for metals and ceramics but low K cvalues because their Young’s modulus is low.
The resistance of a material to fatigue, a process of slow crack growth under repeated stress cycles, is important in several biomedical and engineering applications. Implants used in total joint replacement or in repairing large defects in the long bones of the limbs, for example, are subjected not just to a constant or slowly varying stress but to repeated cyclic stresses as well during normal activities of walking, running, and jumping. Stents used to keep coronary arteries open have to withstand the pressure pulsations of blood flow through the arterial vessels.
Читать дальше

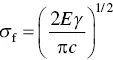

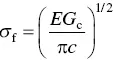
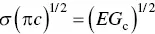
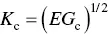
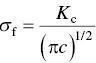
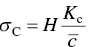
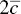 is the average crack length.
is the average crack length.











