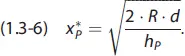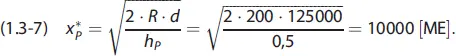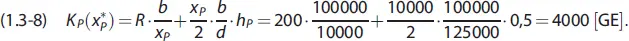
Abb. 1-11: Optimale Bestellmenge und resultierende, minimale Gesamtkosten der Brauerei
Betrachten wir nun die Glashütte, d. h. den Lieferanten der Glasflaschen. Die Glashütte (P) plant ihre Produktions- und Transportpolitik unter dem Ziel der Minimierung ihrer gesamten entscheidungsrelevanten Periodenkosten: die Rüstkosten und die Lagerhaltungskosten. Ein Produktionslos ist die (positive) Quantität eines Gutes, die auf einem Produktionssystem ohne Unterbrechung zu fertigen ist. Zur Fertigung des Produktionsloses muss das Produktionssystem zunächst (um-)gerüstet werden, um für die Fertigung des Produktionsloses einsatzbereit zu sein. Diese Rüstvorgänge beanspruchen Rüstzeit und verursachen Rüstkosten unabhängig von der Quantität (Losgröße) des aufgelegten Produktionsloses. Die Versorgung des nachgelagerten Standorts (der Brauerei) mit dem zu erstellenden Vorprodukt erfolgt aus dem Ausgangslager. Durch die Lagerung der erzeugten Vorprodukte bis zu ihrem Transport zu dem nachgelagerten Standort fallen Lagerhaltungskosten (Lagerkosten i. e. S. und Kapitalbindungskosten) an.
Bezüglich der Produktionspolitik wird angenommen, dass die Glashütte eine so genannte geschlossene Produktion verfolgt, d. h. fertiggestellte Produkteinheiten eines Produktionsloses können erst an die nachfolgende Stufe – den Brauereistandort (A) – weitergegeben werden, nachdem die Bearbeitung des gesamten Produktionsloses abgeschlossen ist. Des Weiteren entspricht die Weitergabe-/Transportmenge dem Produktionslos. Das gesamte Produktionslos wird somit unmittelbar nach Fertigstellung an den Brauereistandort (A) weitergegeben. Diese Produktionspolitik wird aufgrund der losweisen Weitergabe auch Lot-for-Lot Production Strategy genannt (Toomey, 2000).
Die Periodenkapazität der Glashütte (P), gemessen in Mengeneinheiten je Periode, beträgt d [ME/Periode] und der Lagerzugang erfolgt mit einer konstanten Produktionsrate. Es gilt d > b, da für d < b der Bedarf der Brauerei (A) pro Periode nicht befriedigt werden könnte und im Falle von d = b eine kontinuierliche Produktion erfolgen müsste. Der bekannte Gesamtbedarf je Periode b [ME/Periode] der Brauerei (A) kann z. B. durch eine Produktionspolitik mit kleinen Produktionslosgrößen bei hoher Produktions- und Transportfrequenz oder durch eine Produktionspolitik mit großen Losgrößen bei niedriger Produktions- und Transportfrequenz gedeckt werden. In Abhängigkeit der gewählten Losgröße verlaufen die resultierenden entscheidungsrelevanten Rüst- und Lagerhaltungskosten gegenläufig: »To minimize set-up costs requires large batches. To minimize holding costs requires small batches« (Cox/Blackstone, 1997, S. 9.34).
Unter der Annahme einer unendlich schnellen Lieferzeit sowie eines Lagerzugangs mit konstanter Produktionsrate ist der Gesamtbedarf b [ME/Periode] durch 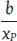 Losauflagen je Periode der identischen Quantität von x p[ME] zu decken. Fehlmengen treten annahmegemäß nicht auf, d. h. die Produktionslosgröße x p[ME] entspricht der Transportmenge. Der Lagerbestandsverlauf beim Lieferanten (P), unter den gegebenen Annahmen, ist in der nachfolgenden Abbildung 1-12 dargestellt. Aufgrund von d > b ergibt sich ein durchschnittlicher Lagerbestand von
Losauflagen je Periode der identischen Quantität von x p[ME] zu decken. Fehlmengen treten annahmegemäß nicht auf, d. h. die Produktionslosgröße x p[ME] entspricht der Transportmenge. Der Lagerbestandsverlauf beim Lieferanten (P), unter den gegebenen Annahmen, ist in der nachfolgenden Abbildung 1-12 dargestellt. Aufgrund von d > b ergibt sich ein durchschnittlicher Lagerbestand von 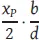 [ME].
[ME].
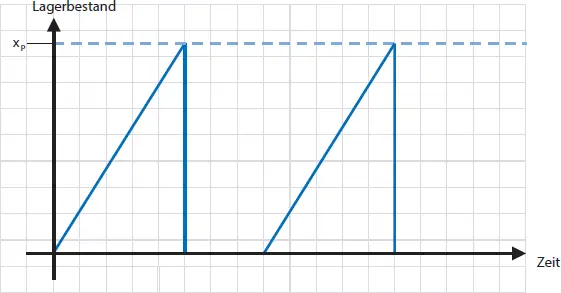
Abb. 1-12: Lagerbestandsverlauf des Lieferanten (P)
Die Rüstkosten, die bei jeder Losauflage in gleicher Höhe anfallen, betragen R [GE] und der Lagerhaltungskostensatz beim Lieferanten (P) beträgt h p[GE/ME und Periode]. Transportkosten berücksichtigt Banerjee (1986) in seinem Beispiel nicht explizit. Im Falle einer Lot-for-Lot-Produktionspolitik ist jedoch die Anzahl der Losauflagen je Periode identisch mit der Anzahl der Transporte je Periode. Der Rüstkostensatz von R [GE] repräsentiert daher die Summe aus Rüst- und Transportkosten je Losauflage und Transport. Mit den pro Periode anfallenden Rüst- und Transportkosten 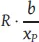 [GE/Periode] und den Lagerkosten
[GE/Periode] und den Lagerkosten 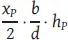 [GE/Periode] ergeben sich die zu minimierenden entscheidungsrelevanten Kosten im Planungszeitraum mit:
[GE/Periode] ergeben sich die zu minimierenden entscheidungsrelevanten Kosten im Planungszeitraum mit:
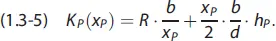
Die optimale Produktions- und Transportlosgröße 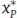 [ME] lässt sich durch Nullsetzen der ersten Ableitung der Funktion (1.3-5) nach x permitteln:
[ME] lässt sich durch Nullsetzen der ersten Ableitung der Funktion (1.3-5) nach x permitteln:
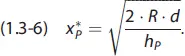
In unserem Beispiel benötigt die Brauerei (A) von der Glashütte (P) b = 100000 Flaschen pro Jahr. Die Jahreskapazität der Glashütte (P) beträgt d = 125000 [ME/Jahr]. Betragen die Rüst- und Transportkosten R = 200 [GE] und ist der Lagerhaltungskostensatz der Glashütte ebenfalls mit h p= 0,5 [GE/ME und Jahr] gegeben, so lautet die optimale Produktions- und Transportlosgröße der Glashütte:
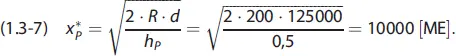
Die Glashütte wählt somit 10-mal pro Jahr eine Losauflage von 10000 Flaschen. Aus entsprechenden Losauflagen und Transporten resultieren die minimalen entscheidungsrelevanten Kosten in Höhe von:
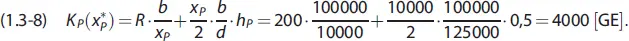
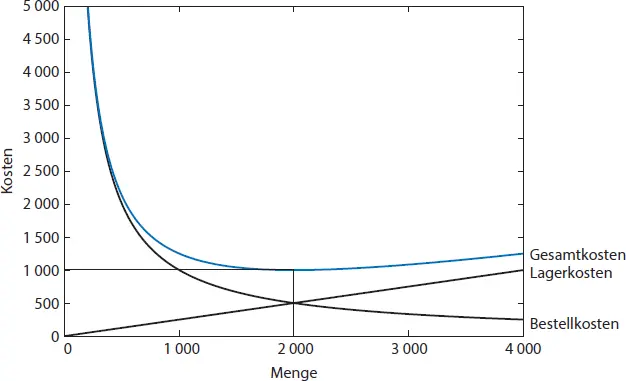
Die folgende Abbildung 1-13 zeigt, dass sich die optimale Produktions- und Transportmenge im Schnittpunkt der entgegengesetzt verlaufenden Lagerkosten einerseits und der Rüst- und Transportkosten andererseits ergibt.
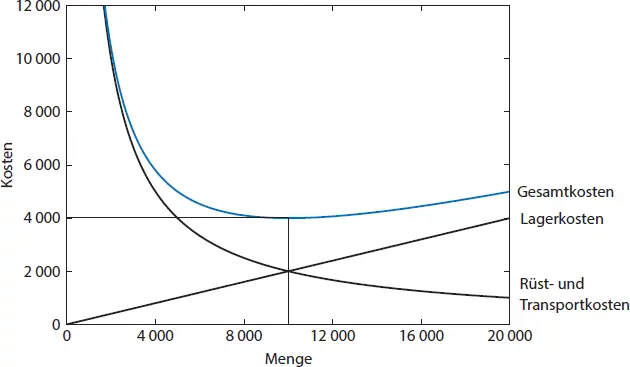
Abb. 1-13: Optimale Produktionspolitik und resultierende, minimale Gesamtkosten der Glashütte
Verfolgt der Lieferant (P) eine Lot-for-Lot-Produktionspolitik, so entspricht die Produktions- und Transportlosgröße x pgenau der Liefermenge an den Abnehmer (A). Beim Abnehmer (A) wiederum entspricht unter den gegebenen Annahmen die Bestellmenge x Agenau der Liefermenge des Lieferanten (P): »This assumption of supply on a lot-by-lot basis implies that the production lot size of the vendor is equal to the order quantity of the purchaser« (Chatterjee/Ravi, 1991, S. 118). Für die Bestellpolitik des Abnehmers (A) und die Produktionspolitik des Lieferanten (P) muss somit x A= x pgelten. Die Lagerbestände des betrachteten Produkts beim Abnehmer (A) und Lieferanten (P), d. h. bei der Brauerei (A) und der Glashütte (P), nehmen für die so genannte integrierte oder gemeinsame Bestell- und Produktionspolitik x G= x A= x pdie in Abbildung 1-14 dargestellten Verläufe an.
Читать дальше


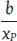 Losauflagen je Periode der identischen Quantität von x p[ME] zu decken. Fehlmengen treten annahmegemäß nicht auf, d. h. die Produktionslosgröße x p[ME] entspricht der Transportmenge. Der Lagerbestandsverlauf beim Lieferanten (P), unter den gegebenen Annahmen, ist in der nachfolgenden Abbildung 1-12 dargestellt. Aufgrund von d > b ergibt sich ein durchschnittlicher Lagerbestand von
Losauflagen je Periode der identischen Quantität von x p[ME] zu decken. Fehlmengen treten annahmegemäß nicht auf, d. h. die Produktionslosgröße x p[ME] entspricht der Transportmenge. Der Lagerbestandsverlauf beim Lieferanten (P), unter den gegebenen Annahmen, ist in der nachfolgenden Abbildung 1-12 dargestellt. Aufgrund von d > b ergibt sich ein durchschnittlicher Lagerbestand von 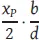 [ME].
[ME].
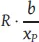 [GE/Periode] und den Lagerkosten
[GE/Periode] und den Lagerkosten 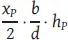 [GE/Periode] ergeben sich die zu minimierenden entscheidungsrelevanten Kosten im Planungszeitraum mit:
[GE/Periode] ergeben sich die zu minimierenden entscheidungsrelevanten Kosten im Planungszeitraum mit: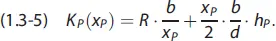
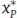 [ME] lässt sich durch Nullsetzen der ersten Ableitung der Funktion (1.3-5) nach x permitteln:
[ME] lässt sich durch Nullsetzen der ersten Ableitung der Funktion (1.3-5) nach x permitteln: