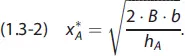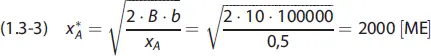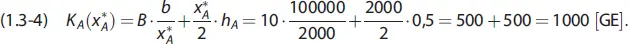»The integration of all key business processes across the supply chain is what we are calling supply chain management« (Cooper/Lambert/Pagh, 1997, S. 11)
Auch im dritten Beispiel – welches hoffentlich ebenfalls dazu motiviert, sich tiefer mit Supply Chain Management zu beschäftigen – geht es um die Koordination arbeitsteiliger Wertschöpfungsprozesse; konkret um die Abstimmung von Produktions-, Transport- und Bestellquantitäten zwischen einem Lieferanten und seinem Abnehmer. Grundlage des Beispiels bildet das von Banerjee (1986) präsentierte JELS-Model (Joint Economic Lot Size Model) zur Bestimmung einer standortübergreifenden, integrierten Losgröße.
Wir betrachten wieder die uns bekannte, arbeitsteilige Bier-Supply Chain, jedoch diesmal den Ausschnitt mit dem Lieferanten für Glasflaschen (hier eine Glashütte) und dem Produzenten (Brauerei), der diese Flaschen in seiner Abfüllanlage verwendet. Zur Vereinfachung betrachten wir Einweg-Bierflaschen, auch wenn dies aus Umweltgesichtspunkten abzulehnen ist (  Abb. 1-9).
Abb. 1-9).
Aktuell existieren in Deutschland zwei Pfandsysteme: Mehrwegpfand und Einwegpfand. Gesetzlich geregelt ist der Einwegpfand insbesondere in § 9 der Verpackungsverordnung (VerpackV). Mehrwegpfand hingegen ist ein freiwilliges System der Getränkeindustrie. Der Unterschied zwischen beiden Systemen besteht darin, dass Mehrwegpfandflaschen wiederverwendet werden, d. h. nach Rückgabe werden die Pfandflaschen umfangreich gereinigt und anschließend neu befüllt. Einwegpfandflaschen hingegen werden zerkleinert und recycelt.
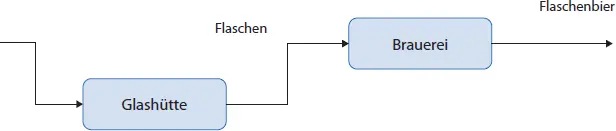
Abb. 1-9: Ausschnitt der Bier-Supply Chain
Wird ein bestimmtes Produkt im Rahmen eines mehrstufigen, arbeitsteiligen Produktionsprozesses erzeugt und erfolgen die einzelnen Teilprozesse an räumlich getrennten Standorten (Werken) eines oder unterschiedlicher Unternehmen, so stellt sich das Problem der standortübergreifenden (werksübergreifenden) und wohlmöglich unternehmensübergreifenden Losgrößenplanung. Um mögliche Lösungen dieses Planungsproblems beurteilen zu können, legen wir als außenstehender Betrachter das Zielkriterium derart fest, dass sämtliche Teilproduktionsprozesse so zu koordinieren sind, dass die relevanten Gesamtkosten in dem betrachteten Ausschnitt der Bier-Supply Chain minimiert werden (Formalziel), bei vollständiger Erfüllung der Kundenanforderungen (Sachziel). Schließlich werden wir das Beispiel möglichst simpel und mathematisch einfach gestalten – für eine umfassende, spieltheoretische Analyse dieses Problems sei auf Sucky (2004b und 2004c) verwiesen.
Betrachten wir zunächst den Abnehmer, d. h. die Brauerei. Es ist festzulegen, wie oft im Planungszeitraum die fremdbezogenen Glasflaschen bestellt werden und wie hoch die jeweilige Bestellmenge ist. Zur Ermittlung dieser Bestellpolitik des Abnehmers (A) – als auch später zur Ermittlung der Produktions- und Transportpolitik des Lieferanten (P) – kann das von Harris (1913) für den Produktionsbereich entwickelte, von Stefanič-Allmayer (1927) auf den Beschaffungsbereich übertragene, aber erst durch Andler (1929) im deutschen Sprachraum bekannt gewordene Grundmodell der Losgrößenplanung (Andler-Formel, Economic Order Quantity, EOQ-Formel) herangezogen werden. Die Brauerei (A) plant ihre Bestellpolitik unter dem Ziel der Minimierung ihrer gesamten entscheidungsrelevanten Periodenkosten: die Bestellkosten und die Lagerhaltungskosten. Die variablen Beschaffungskosten je Stück werden als im Planungszeitraum konstant angenommen und sind daher nicht entscheidungsrelevant.
Der bekannte Gesamtbedarf je Periode b [ME/Periode] kann z. B. durch eine Bestellpolitik mit geringen Bestellquantitäten bei hoher Bestellfrequenz oder durch eine Bestellpolitik mit großen Bestellquantitäten bei niedriger Bestellfrequenz gedeckt werden. In Abhängigkeit der damit verbundenen Bestellquantitäten und -frequenz verlaufen die resultierenden entscheidungsrelevanten Bestell- und Lagerhaltungskosten gegenläufig. Gesucht ist die Bestellpolitik, die über einen Ausgleich dieser gegenläufigen Tendenz zu den minimalen gesamten entscheidungsrelevanten Periodenkosten führt. Unter der Annahme einer unendlich schnellen Lieferzeit sowie eines kontinuierlichen Lagerabgangs mit einer konstanten Nachfragerate ist der Gesamtbedarf b [ME/Periode] durch 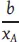 Bestellungen je Periode der identischen Quantität von x A[ME] zu decken. Fehlmengen treten annahmegemäß nicht auf, d. h. die Bestellmenge x A[ME] entspricht der Liefermenge und der Lagereingangsmenge. Erfolgt der Lagerabgang kontinuierlich, so beträgt der durchschnittliche Lagerbestand
Bestellungen je Periode der identischen Quantität von x A[ME] zu decken. Fehlmengen treten annahmegemäß nicht auf, d. h. die Bestellmenge x A[ME] entspricht der Liefermenge und der Lagereingangsmenge. Erfolgt der Lagerabgang kontinuierlich, so beträgt der durchschnittliche Lagerbestand 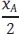 [ME]. Der Lagerbestandsverlauf beim Abnehmer (A), unter den gegebenen Annahmen, ist in Abbildung 1-10 dargestellt.
[ME]. Der Lagerbestandsverlauf beim Abnehmer (A), unter den gegebenen Annahmen, ist in Abbildung 1-10 dargestellt.
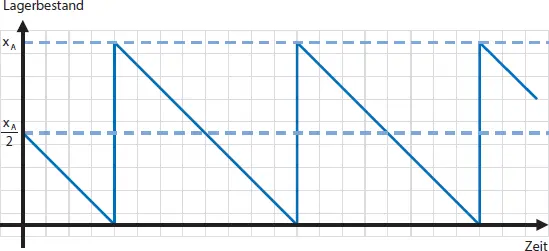
Abb. 1-10: Lagerbestandsverlauf des Abnehmers (A)
Pro Bestellung fallen Kosten in Höhe von B [GE] an und der Lagerhaltungskostensatz beim Abnehmer (A) beträgt h A[GE/ME und Periode]. Mit den pro Periode anfallenden Bestellkosten 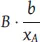 [GE/Periode] und Lagerkosten
[GE/Periode] und Lagerkosten 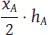 [GE/Periode] ergeben sich die zu minimierenden entscheidungsrelevanten Kosten im Planungszeitraum mit:
[GE/Periode] ergeben sich die zu minimierenden entscheidungsrelevanten Kosten im Planungszeitraum mit:
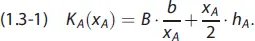
Die optimale Bestellmenge 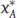 [ME] lässt sich durch Nullsetzen der ersten Ableitung der Funktion (1.3-1) nach x Aermitteln:
[ME] lässt sich durch Nullsetzen der ersten Ableitung der Funktion (1.3-1) nach x Aermitteln:
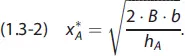
In unserem Beispiel benötigt die Brauerei (A) 100000 Flaschen pro Jahr. Betragen die Bestellkosten B = 10 [GE] und ist der Lagerhaltungskostensatz mit h A= 0,5 [GE/ME und Jahr] gegeben, so lautet die optimale Bestellmenge der Brauerei:
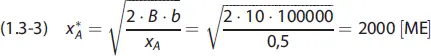
Die Brauerei möchte somit 50-mal pro Jahr mit jeweils 2000 Flaschen beliefert werden. Aus entsprechenden Bestellungen und Lieferungen resultieren die minimalen entscheidungsrelevanten Kosten in Höhe von:
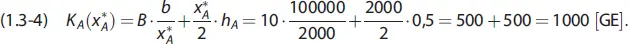
Die folgende Abbildung 1-11 zeigt, dass sich die optimale Bestellmenge im Schnittpunkt der entgegengesetzt verlaufenden Lager- und Bestellkostenkurven ergibt.
Читать дальше

 Abb. 1-9).
Abb. 1-9).
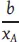 Bestellungen je Periode der identischen Quantität von x A[ME] zu decken. Fehlmengen treten annahmegemäß nicht auf, d. h. die Bestellmenge x A[ME] entspricht der Liefermenge und der Lagereingangsmenge. Erfolgt der Lagerabgang kontinuierlich, so beträgt der durchschnittliche Lagerbestand
Bestellungen je Periode der identischen Quantität von x A[ME] zu decken. Fehlmengen treten annahmegemäß nicht auf, d. h. die Bestellmenge x A[ME] entspricht der Liefermenge und der Lagereingangsmenge. Erfolgt der Lagerabgang kontinuierlich, so beträgt der durchschnittliche Lagerbestand 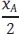 [ME]. Der Lagerbestandsverlauf beim Abnehmer (A), unter den gegebenen Annahmen, ist in Abbildung 1-10 dargestellt.
[ME]. Der Lagerbestandsverlauf beim Abnehmer (A), unter den gegebenen Annahmen, ist in Abbildung 1-10 dargestellt.
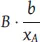 [GE/Periode] und Lagerkosten
[GE/Periode] und Lagerkosten 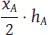 [GE/Periode] ergeben sich die zu minimierenden entscheidungsrelevanten Kosten im Planungszeitraum mit:
[GE/Periode] ergeben sich die zu minimierenden entscheidungsrelevanten Kosten im Planungszeitraum mit: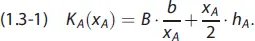
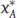 [ME] lässt sich durch Nullsetzen der ersten Ableitung der Funktion (1.3-1) nach x Aermitteln:
[ME] lässt sich durch Nullsetzen der ersten Ableitung der Funktion (1.3-1) nach x Aermitteln: