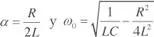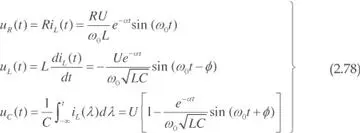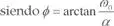Para t > 0, en que el interruptor Sl· está cerrado y S2 abierto, aplicando la ley de Kirchhoff de tensiones a la malla resultante, se puede escribir:

Siendo I L(0) = I LOla corriente en el inductor en el instante inicial t = 0 y 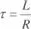 la constante de tiempo del circuito, la solución de la ecuación (2.66) es:
la constante de tiempo del circuito, la solución de la ecuación (2.66) es:
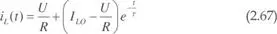
La tensión en el inductor será:
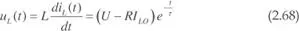
En la figura 2.39.b se muestra la evolución de la corriente y la tensión en el inductor, observando la variación exponencial desde el valor inicial hasta el final.
Descarga del circuito RL
Sea el circuito de la figura 2.40.a, cuyo inductor se está cargando a través de la resistencia R y el interruptor S 1En el instante t = 0, se cierra el interruptor S2 al mismo tiempo que se abre el interruptor S 1Se inicia la descarga del inductor L .
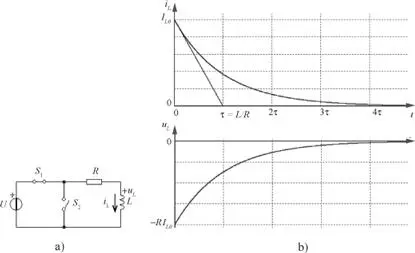
Figura 2.40. Transitorio en la descarga de un circuito de primer orden RL.
Para t > 0, en que el interruptor S2 está cerrado y Sl· abierto, aplicando la ley de Kirchhoff de tensiones a la malla resultante, se puede escribir:

Siendo I,LO la tensión en el condensador en el instante inicial 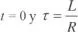 la constante de tiempo del circuito, la solución de la ecuación (2.69) es:
la constante de tiempo del circuito, la solución de la ecuación (2.69) es:

La tensión en el inductor será:
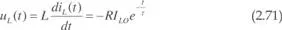
En la figura 2.40.b se muestra la evolución de la corriente y la tensión en el inductor.
2.4.3. Circuitos de segundo orden
Carga del circuito RLC,
Sea el circuito serie RLC de la figura 2.41.a, que se supondrá totalmente descargado en el instante t = 0 en que se cierra el interruptor S1 al mismo tiempo que se abre el interruptor S 2. Se inicia la carga del condensador C.
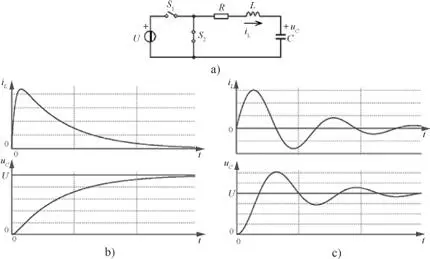
Figura 2.41. Circuito de primer orden RLC. Carga
Para t > 0, en que el interruptor S1 está cerrado y S2 abierto, aplicando la ley de Kirchhoff de tensiones a la malla resultante, se puede escribir:
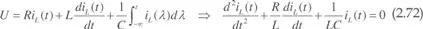
La solución de la ecuación 2.72 es:

siendo A1 y A2 constantes de integración y rl y r 2las raíces de la ecuación
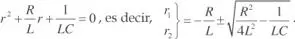
Se pueden presentar tres casos:
a) Si 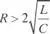 , las raíces son reales y diferentes y la solución es una onda aperiódica unidireccional
, las raíces son reales y diferentes y la solución es una onda aperiódica unidireccional
b) Si 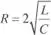 , la raíz es doble y la solución es una onda aperiódica unidireccional.
, la raíz es doble y la solución es una onda aperiódica unidireccional.
c) Si 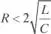 , las raíces son complejas y la solución es una onda periódica bidireccional amortiguada
, las raíces son complejas y la solución es una onda periódica bidireccional amortiguada
a)En el caso de raíces reales diferentes la solución es:

siendo 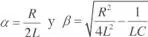
Las tensiones en los componentes son:
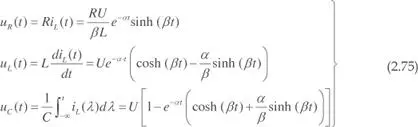
En la figura 2.41.b se muestra la evolución de la corriente en el inductory la tensión en el condensador.
b)En el caso de raíz real doble la solución es:

siendo 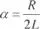 . Se trata de un caso de difícil existencia física, de comportamiento análogo al caso a) con raíces que fueran muy parecidas.
. Se trata de un caso de difícil existencia física, de comportamiento análogo al caso a) con raíces que fueran muy parecidas.
c)En el caso de raíces complejas, la solución es:

siendo 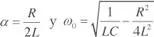
Las tensiones en los componentes son:
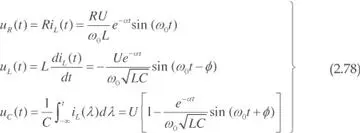
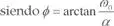
En la figura 2.41.c se muestra la evolución de la corriente en el inductor y la tensión en el condensador.
Читать дальше


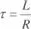 la constante de tiempo del circuito, la solución de la ecuación (2.66) es:
la constante de tiempo del circuito, la solución de la ecuación (2.66) es: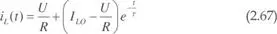
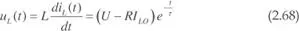


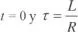 la constante de tiempo del circuito, la solución de la ecuación (2.69) es:
la constante de tiempo del circuito, la solución de la ecuación (2.69) es:
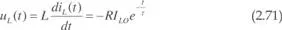

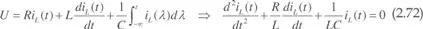

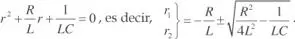
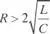 , las raíces son reales y diferentes y la solución es una onda aperiódica unidireccional
, las raíces son reales y diferentes y la solución es una onda aperiódica unidireccional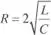 , la raíz es doble y la solución es una onda aperiódica unidireccional.
, la raíz es doble y la solución es una onda aperiódica unidireccional.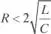 , las raíces son complejas y la solución es una onda periódica bidireccional amortiguada
, las raíces son complejas y la solución es una onda periódica bidireccional amortiguada
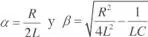
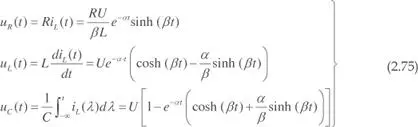

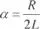 . Se trata de un caso de difícil existencia física, de comportamiento análogo al caso a) con raíces que fueran muy parecidas.
. Se trata de un caso de difícil existencia física, de comportamiento análogo al caso a) con raíces que fueran muy parecidas.