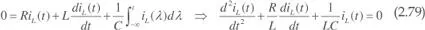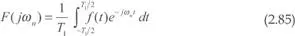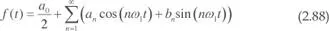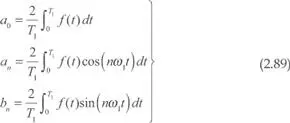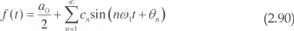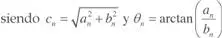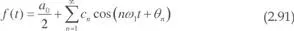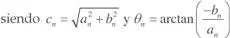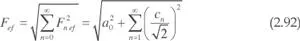Robert Piqué López - Electrónica de potencia

Descarga del circuito RLC

Sea el circuito serie RLC de la figura 2.42.a, del que se supondrá que el condensador está totalmente cargado a la tensión U. En el instante t = 0 se abre el interruptor S 1al mismo tiempo que se cierra el interruptor S 2Se inicia la descarga del condensador C.

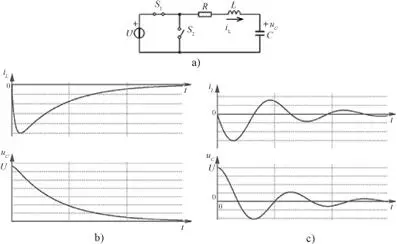
Figura 2.42. Circuito de primer orden RLC. Descarga.

Para t > 0 en que el interruptor S 1está abierto y S 2cerrado, aplicando la ley de Kirchhoff de tensiones a la malla resultante, se puede escribir:

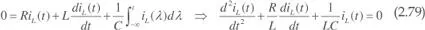
Se observa que se trata de la misma ecuación diferencial que se obtuvo para el circuito de la figura 2.35.a (ecuación 2.72), con la única diferencia en la condición inicial del condensador que, en este caso, está cargado a la tensión U.

La corriente que se establecerá será igual a la que se estableció en el circuito de la figura 2.41.a, pero en este caso circula en sentido inverso. Las dos corrientes únicamente difieren en el signo. En el circuito de la figura 2.41.a se produjo la carga del condensador de cero a U mientras que en este caso se producirá la descarga de U a cero.

Les tensiones en la resistencia y en la inductancia también son las mismas con la única diferencia en el signo y únicamente la tensión en el condensador es diferente. En efecto, en este caso resulta:

En consecuencia, las diferentes expresiones resultan:

En la figura 2.42.b se muestra la evolución de la corriente en el inductor y la tensión en el condensador.

En la figura 2.42.c se muestra la evolución de la corriente en el inductor y la tensión en el condensador.

Sea f(t ) una función periódica de período T1 (frecuencia f 1=1/ T 1y pulsación ω1 = 2π f 1, no sinusoidal. Se denomina transformación integral de Fourier

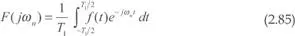
A partir de (2.85) se deriva que la función periódica f ( t ) se puede descomponer en una suma de infinitos términos sinusoidales de frecuencias múltiplos de f 1y de amplitudes dadas por el módulo de F 1= jω nde acuerdo con la siguiente expresión (expansión en serie de Fourierde ft)):

expresión que de acuerdo con las identidades de Euler

se puede desarrollar como

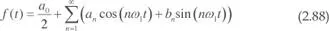
con ω 1= 2π T 1ysiendo a0, an y bn los llamados coeficientes de Fourier que se calculan de la siguiente forma:

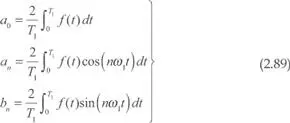
Dado que los senos y cosenos de la misma frecuencial se pueden combinar en una misma sinusoide, la serie de Fourier se puede poner en la forma:

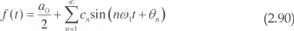
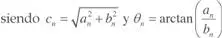
También se puede poner en la forma:

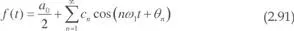
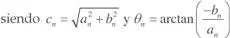
Como se aprecia, el parámetro a0/2 es una constante cuyo valor es el valor medio de la función f ( t ). El parámetro c1 es la amplitud del término sinusoidal de igual pulsación ω1 que f ( t ), es el denominado termino fundamental o primer armónico. Los parámetros c2, c3... son las amplitudes de los distintos armónicos de frecuencias 2 ω 1, 3 ω 1…, respectivamente.

El valor eficaz de f ( t ) se puede calcular a partir de la serie de Fourier, resultando:

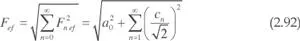
Determinadas simetrías de la función f(t ) dan lugar a una reducción considerable del número de términos de la serie de Fourier. En la tabla 2.5 se indican los coeficientes resultantes para cada simetría así como las funciones que aparecen en la serie.

Tabla 2.5. Coeficientes de Fourier en ondas simétricas.

a. Simetría par

Una función se dice con simetría par si su gráfica es simétrica respecto del eje de ordenadas, es decir, la función f ( t ) es de simetría par si f ( t ) = f(– t ).

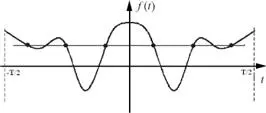
Figura 2.43. Onda con simetría par.

b. Simetría impar

Una función se dice que es con simetría impar si su gráfica es simétrica respecto origen, es decir, la función f ( t ) es de simetría impar si – f ( t ) = f (—t).

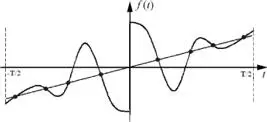
Figura 2.44. Onda con simetría impar.