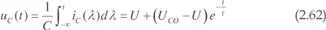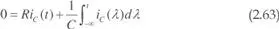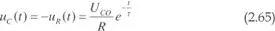d)Por último, una vez hallada la estructura dual, deben definirse los signos de las magnitudes duales, la polaridad de las fuentes de tensión y la dirección de las fuentes de corriente. Por ejemplo, en el caso de la figura 2.36.b, el signo de la fuente de corriente I’. Para ello, se deberán orientar las ramas del circuito inicial y deducir la orientación del circuito dual. Con la orientación elegida, la ley de mallas para el circuito de la figura 2.36.a permite escribir:
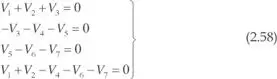
siendo V ila tensión de la rama i.
Por dualidad, estas ecuaciones son coincidentes con las ecuaciones de nodo del circuito dual. Así en los nudos A, B, C y D se cumplirá que:

De estas últimas ecuaciones se deducen directamente la orientación de las ramas del circuito de la figura 2.36.b. Conocer la orientación de estas ramas es fundamental en el caso de la presencia de componentes unidireccionales como el diodo, como es el caso presentado en la figura 2.36.
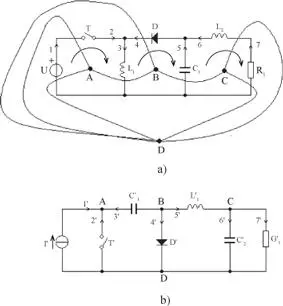
Figura 2.36. Búsqueda del circuito dual.
Sin necesidad de plantear la ecuaciones de malla, se puede determinar la polaridad de las fuentes de tensión y la dirección de las fuentes de corriente, aplicando la siguiente regla: una fuente de tensión que produce una corriente de malla positiva (en el sentido del movimiento de las agujas del reloj) tiene como su dual una fuente de corriente cuya dirección es del nodo de referencia al nodo de no referencia.
2.4. Regímenes transitorios
2.4.1. Introducción
En los circuitos en tiempo continuo disipativos excitados por magnitudes periódicas o constantes a partir de un determinado instante t = t 0, con el paso de un tiempo finito o infinito T RT, el sistema alcanza el denominado régimen permanente(o estado estacionario),caracterizado porque a partir del instante t = t 0+T RTtodas las magnitudes son periódicas, es decir que presentan el mismo valor al inicio y al final de cada período. Esto no sucede durante el intervalo t0 ≤ t ≤ t0 + TRT, constituyendo el denominado régimen transitoriodel circuito. Si TRT= 0, caso propio de los circuitos resistivos, se dice que el circuito no tiene dinámica, denominándose circuito con dinámica en el caso contrario.
Siendo un convertidor estático un sistema formado básicamente por interruptores, su funcionamiento en régimen permanente estará formado por una sucesión de regímenes transitorios, debido a que el sistema presentará diferentes topologías con el paso del tiempo, cada uno de ellos provocado por la abertura o cierre de un interruptor, por lo que a este régimen particular se le denomina régimen permanente estático,un caso específico de los convertidores estáticos.
En apartados sucesivos se analizarán los transitorios que se producen en la carga y descarga de circuitos lineales de primer y segundo orden.
2.4.2. Circuitos de primer orden
Carga del circuito RC
Sea el circuito de la figura 2.37.a, cuyo condensador se está descargando a través de la resistencia R y el interruptor S 2. En el instante t = 0, se cierra el interruptor S1 al mismo tiempo que se abre el interruptor S 2Se inicia la carga del condensador C.
Para t > 0, en que el interruptor S 1está cerrado y S 2abierto, aplicando la ley de Kirchhoff de tensiones a la malla resultante, se puede escribir:
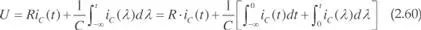
Siendo 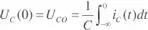 la tensión en el condensador en el instante inicial t = 0 y τ = RC la constante de tiempo del circuito, la solución de la ecuación (2.60) es:
la tensión en el condensador en el instante inicial t = 0 y τ = RC la constante de tiempo del circuito, la solución de la ecuación (2.60) es:

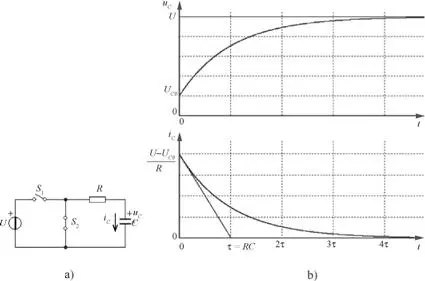
Figura 2.37. Transitorio en la carga de un circuito de primer orden RC.
La tensión en el condensador se obtiene de la siguiente forma:
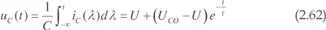
En la figura 2.37.b, se muestra la evolución de la tensión y la corriente en el condensador, observando la variación exponencial desde el valor inicial hasta el final.
Descarga del circuito RC
Sea el circuito de la figura 2.38.a, cuyo condensador se está cargando a través de la resistencia R y el interruptor S 1. En el instante t = 0, se cierra el interruptor S 2al mismo tiempo que se abre el interruptor S 1. Se inicia la descarga del condensador C.
Para t > 0, en que el interruptor S 2está cerrado y S 1abierto, aplicando la ley de Kirchhoff de tensiones a la malla resultante, se puede escribir:
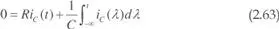
Siendo UCO la tensión en el condensador en el instante inicial t = 0 y τ = RC la constante de tiempo del circuito, la solución de la ecuación (2.63) es:

La tensión en el condensador será:
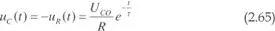
En la figura 2.38.b se muestra la evolución de la tensión y la corriente en el condensador.
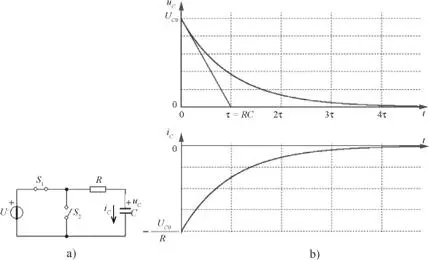
Figura 2.38. Transitorio en la descarga de un circuito de primer orden RC.
Carga del circuito RL
Sea el circuito de la figura 2.39.a, cuyo inductor se está descargando a través de la resistencia R y el interruptor S2. En el instante t = 0, se cierra el interruptor S 1al mismo tiempo que se abre el interruptor S 2. Se inicia la carga del inductor L.
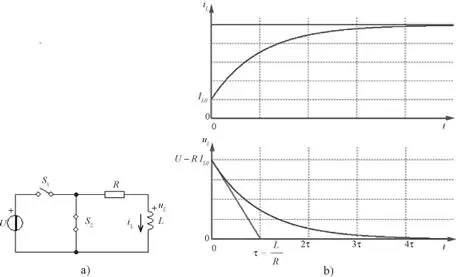
Figura 2.39. Transitorio en la carga de un circuito de primer orden RL.
Читать дальше

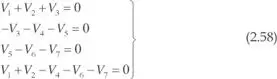


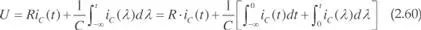
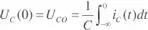 la tensión en el condensador en el instante inicial t = 0 y τ = RC la constante de tiempo del circuito, la solución de la ecuación (2.60) es:
la tensión en el condensador en el instante inicial t = 0 y τ = RC la constante de tiempo del circuito, la solución de la ecuación (2.60) es: