c. Simetría de media onda
Una función f ( t ) periódica, de período T 1, se dice que es de simetría de media onda si: 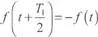 es decir, si en su gráfica la parte positiva es un reflejo de la negativa pero desplazada medio período.
es decir, si en su gráfica la parte positiva es un reflejo de la negativa pero desplazada medio período.
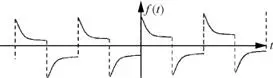
Figura 2.45. Onda con simetría de media onda.
d. Simetría de cuarto de onda par
Una función se dice que es de simetría de cuarto de onda par si tiene simetría de media onda y además es una función con simetría par.
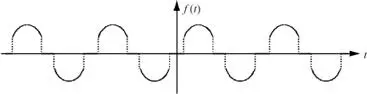
Figura 2.46. Onda con simetría de cuarto de onda par.
e. Simetría de cuarto de onda impar
Una función se dice de simetría de cuarto de onda impar si tiene simetría de media onda y además es una función con simetría impar.
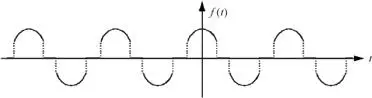
Figura 2.47. Onda con simetría par de cuarto de onda impar.
En la tabla 2.6 se indican las series de Fourier de algunas funciones de uso habitual.
Tabla 2.6. Series de Fourier de ondas habituales.
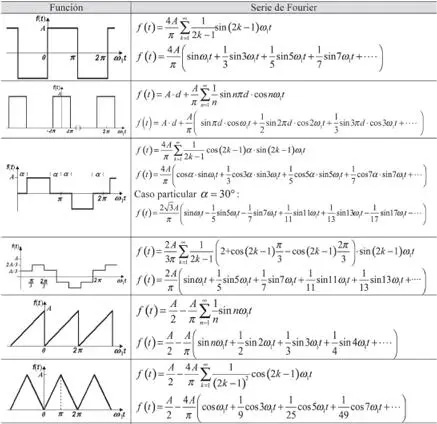
Tabla 2.6 Continuación.

2.5.2. Dominio del tiempo y dominio de la frecuencia
Dada una función periódica f ( t ), le corresponde una y sólo una serie de Fourier, es decir, le corresponde un conjunto único de coeficientes Cn. Es por ello que los coeficientes Cn especifican a f ( t ) en el dominio de la frecuenciade la misma manera que f ( t ) especifica la función en el dominio del tiempo.
A la gráfica de la magnitud de los coeficientes Cn, en función de la frecuencia ω del término correspondiente se le llama el espectro de amplitudde f ( t ).
A la gráfica del ángulo de fase θn, en función de la frecuencia ω del término correspondiente se le llama el espectro de fasede f ( t ).
Nótese que ambas gráficas son funciones discretas, definidas únicamente para valores de frecuencias múltiplos de la frecuencia ω1 del término fundamental.
En resumen, que si f(t) es una función periódica de tiempo continuo, su expansión en serie de Fourier, tanto el módulo como la fase, son funciones aperiódicas y discretas:

Dada la función u(t) = 100sign[sin (100πt)], representarla en el dominio temporal y en el dominio frecuencial.
Solución
La función indicada es una onda cuadrada de amplitud 100 y frecuencia 50 Hz y está representada en la figura E2.7.1.
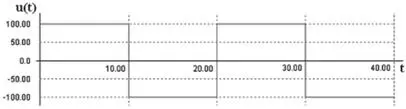
Figura E2.7.1
Por la simetría de la onda (de cuarto de onda impar) la serie de Fourier sólo contiene senos impares, según se indica en la expresión:
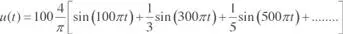
En la figura 2.7.2 se han representado, en el dominio temporal, los cuatro primeros armónicos de frecuencias 50, 150, 250 y 350, así como la suma de todos ellos. Se observa como esta suma ya es una primera aproximación de la función u(t ). A ella se aproximará cada vez más a medida que añadan más armónicos.
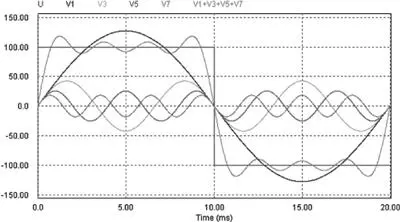
Figura E2.7.2
Las amplitudes de los sucesivos armónicos representados en función de la frecuencia, da el espectro de frecuencias de amplitud de la figura E2.7.3 (simulación PSIM). Nótese que ésta es una función aperiódica y discreta.
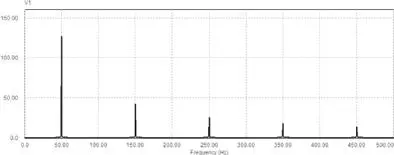
Figura E2.7.3
2.5.3. Transformada de Fourier
La serie de Fourier permite obtener una representación en el dominio de la frecuencia para f unciones periódicas f(t ). Cabe preguntarse si es posible extender de alguna manera las series de Fourier para obtener la representación en el dominio de la frecuencia de funciones no periódicas.
La solución a esta cuestión se resuelve mediante la denominada transformada de Fourier,una función de variable compleja, generalización de (2.85) para cualquier tipo de funciones en tiempo continuo, f ( t ), y definida por
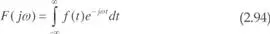
La función F(ω) es una función compleja de la frecuencia (o pulsación) w, y se puede representar por

donde 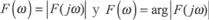 . Las representaciones gráficas de F(ω) y de f (ω) se denominan, respectivamente, espectro de amplitudy espectro de fasede f ( t ), y resultan ser funciones continuas y aperiódicas de la pulsación ω.
. Las representaciones gráficas de F(ω) y de f (ω) se denominan, respectivamente, espectro de amplitudy espectro de fasede f ( t ), y resultan ser funciones continuas y aperiódicas de la pulsación ω.
La transformada de Fourier se utiliza profusamente para el estudio frecuencial de sistemas. No obstante, en los procesos de medida o en cálculo apoyado en ordenador, las funciones temporales no lo son en tiempo continuo sino que son funciones de tiempo discreto, ya que únicamente existen en aquellos instantes de tiempo en los que el sistema reconoce su valor.
De hecho, no es posible, físicamente, observar magnitudes periódicas, dado que únicamente se dispone de un intervalo temporal finito como período de observación. Por ello, es práctica habitual considerar que las magnitudes físicas, observadas durante un intervalo temporal TO, aunque puedan presentar repetibilidad periódica, T 1, en dicho intervalo, son aperiódicas y discretas (numéricas) como consecuencia del proceso de observación y medida o cálculo. En estas condiciones no es aplicable (2.94) sino que dicha expresión debe remplazarse por la denominada transformada discreta de Fourier,una función discreta, periódica y de simetría par, aproximada por la expresión
Читать дальше

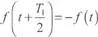 es decir, si en su gráfica la parte positiva es un reflejo de la negativa pero desplazada medio período.
es decir, si en su gráfica la parte positiva es un reflejo de la negativa pero desplazada medio período.






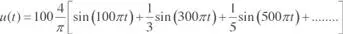


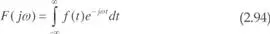

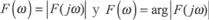 . Las representaciones gráficas de F(ω) y de f (ω) se denominan, respectivamente, espectro de amplitudy espectro de fasede f ( t ), y resultan ser funciones continuas y aperiódicas de la pulsación ω.
. Las representaciones gráficas de F(ω) y de f (ω) se denominan, respectivamente, espectro de amplitudy espectro de fasede f ( t ), y resultan ser funciones continuas y aperiódicas de la pulsación ω.