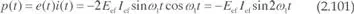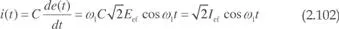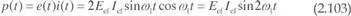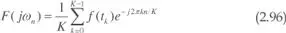
expresión que permite determinar el n-ésimo componente frecuencial de la función temporal f ( t ) definida por K valores discretos f(tk ) en el intervalo de observación TO.
El cálculo de la transformada discreta de Fourier implica un número grande de operaciones, por lo que habitualmente se determina mediante el algoritmo en mariposa desarrollado [11] en 1965 por Cooley y Tukey denominado transformada rápida de Fourier (FFT, Fast Fourier Transform)basado en utilizar un número de K puntos en potencias de 2, y descomponer (2.96) en diversas transformadas elementales. Los programas de simulación como PSIM, utilizan este procedimiento para la representación frecuencial de las magnitudes, acotando su respuesta para frecuencias positivas y eliminado la periodicidad teórica de la transformada calculada.
2.6. Potencias en un régimen periódico
2.6.1. Potencias en un régimen sinusoidal permanente
• Circuito con carga resistiva pura
Considérese el circuito indicado en la figura 2.48, donde 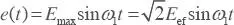 , es decir, es una tensión sinusoidal de valor eficaz e efy pulsación ω 1.
, es decir, es una tensión sinusoidal de valor eficaz e efy pulsación ω 1.
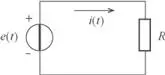
Figura 2.48. Circuito óhmico.
En estas condiciones, la corriente que circulará por el resistor R vendrá dada por:
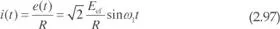
es decir, es una corriente sinusoidal de pulsación ω 1 y valor eficaz 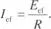
Así pues, la potencia instantánea disipada por el resistor vendrá dada por:
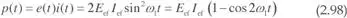
siendo su aspecto el indicado en la figura 2.49.
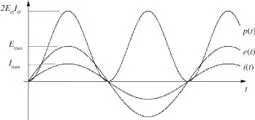
Figura 2.49. Formas de onda en el caso de resistencia óhmica.
El valor medio de esta potencia es:
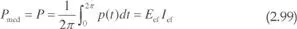
Se llama potencia activa, P,al valor medio de la potencia instantánea, coincidiendo, en caso de carga resistiva pura, con el producto de los valores eficaces de tensión y corriente.
En este caso la interpretación física es que la fuente ha de suministrar una potencia que en valor medio vale EefIef , potencia que es absorbida por la carga y disipada totalmente en forma de calor. Se trata, por tanto, de una potencia útil.
• Circuito con carga inductiva pura
Considérese seguidamente el circuito indicado a la figura 2.50, con la misma excitación de tensión definida por 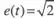 Eefsin ω 1t y carga inductiva pura L.
Eefsin ω 1t y carga inductiva pura L.
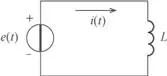
Figura 2.50. Circuito inductivo puro.
En este caso, la corriente que circulará por la inductancia vendrá dada por:
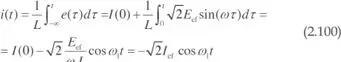
suponiendo la inductancia descargada en el instante inicial ( I(0) = 0), siendo 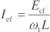 el valor eficaz de la corriente.
el valor eficaz de la corriente.
En este caso, la potencia instantánea vendrá dada por:
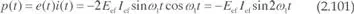
y está representada en la figura 2.51, en la que se aprecian las formas de onda temporales y la representación fasorial 4de la tensión y de la corriente. Se puede apreciar que, en este caso, el valor medio de la potencia es nulo. En efecto, la inductancia es un elemento no disipativo (reactivo), y en el caso ideal planteado se trata de un proceso energético en el que en un cuarto de período la fuente recupera la energía entregada a la inductancia en el cuarto de período precedente.
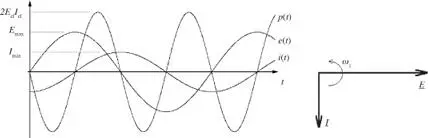
Figura 2.51. Formas de onda en el caso inductivo puro.
• Circuito con carga capacitiva pura
Si ahora se considera el circuito indicado a la figura 2.52, donde de nuevo e(t) = 2 Eef, sinωt 1,
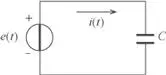
Figura 2.52. Circuito capacitivo puro.
la corriente que circulará será:
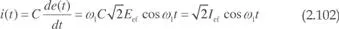
siendo I ef= ω 1 CEef el valor eficaz de la corriente. En esta ocasión, la expresión de la potencia instantánea es:
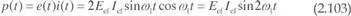
donde, al igual que en el caso de inductancia pura, se obtiene un valor medio nulo, de forma que el proceso energético que tiene lugar (elemento reactivo) indica que en un cuarto de período la fuente recupera la energía entregada al condensador en el cuarto de período precedente.
La figura 2.53 muestra el aspecto de las formas de onda implicadas en este proceso así como el diagrama fasorial de las magnitudes primarias.
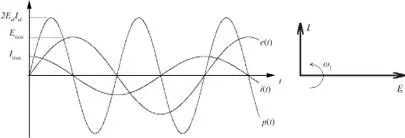
Figura 2.53. Formas de onda en el caso capacitivo puro.
Читать дальше

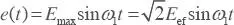 , es decir, es una tensión sinusoidal de valor eficaz e efy pulsación ω 1.
, es decir, es una tensión sinusoidal de valor eficaz e efy pulsación ω 1.
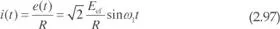
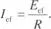
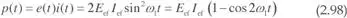

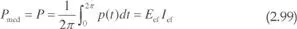
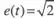 Eefsin ω 1t y carga inductiva pura L.
Eefsin ω 1t y carga inductiva pura L.
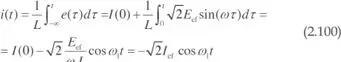
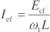 el valor eficaz de la corriente.
el valor eficaz de la corriente.